淺談復變函數的可微性與解析性

高喜花

（河南水利與環境職業學院，河南鄭州450011）

淺談復變函數的可微性與解析性

高喜花

（河南水利與環境職業學院，河南鄭州450011）

本文主要介紹復變函數的可微性與解析性，并利用柯西－黎曼方程推出它們成立的充分條件、必要條件和充要條件，最后歸納總結出復變函數的可微性與解析性的聯系與區別.

復變函數；可微性；解析性；解析函數；柯西－黎曼方程

在復變函數教學中，解析函數是復變函數論研究的主要對象，它是一種具有某種特性的可微函數.函數的解析性與可微性是一個學習重點，也是易混淆的學習難點.文章對這部分內容進行了思考總結，指出復變函數可微性與解析性的聯系與區別，從而有利于更好地理解和掌握復變函數.

1 復變函數的可微性

1.1 復變函數可微性的定義

定義1.1設函數w=f(z)在點z0的鄰域內（或含z0的區域D內）有定義，若極限

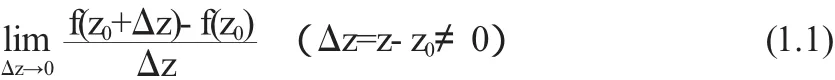
存在，則稱此極限為函數f(z)在點z0的導數，記為f'(z0)這時也稱f(z)在點z0可導.

定義1.2若函數w=f(z)在點z0可導，則稱f'(z0)Δz為函數w=f(z)在點z0的微分，記為

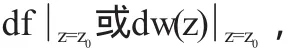
即

此時也稱f(z)在點z0可微.

特別地，當f(z)=z時，dz=Δz，于是(1.2)變為

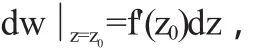
即

由此可見，在復變函數中f(z)在點z0可導與f(z)在點z0可微是等價的.

函數由f(z)在點z可導與可微的概念與數學分析中的可導與可微這兩個概念相類似，因此數學分析中求導基本公式，均可類似地推廣到復變函數中來.同時，與數學分析中一樣，函數f(z)在點z可微，則f(z)在點z連續，反之不一定成立，但在數學分析中，要構造一個處處連續又處處不可微的例子是一件非常困難的事情，而在復變函數中，這樣的例子卻幾乎是隨手可得.如果函數f(z)在區域D內每一點都可微，則稱f(z)在區域D內可微.

1.2 柯西－黎曼方程

設w=f(z)=u(x,y)+iv(x,y)下面我們來探討f(z)的可微性與二元實函數u(x,y)及v(x,y)之間存在的關系.

若f(zz)=u(x,y)+iv(x,y)在點z=x+iy可微，且設

又設

其中

則(1.3)變為

由于當Δz=Δx+iΔy不論按什么方向趨于零時，(1.4)式總是成立，因此我們可以先設Δy=0,Δx→0，即點z+Δz沿著平行于實軸的方向趨于點z（圖1），

圖1

則此時(1.4)變為

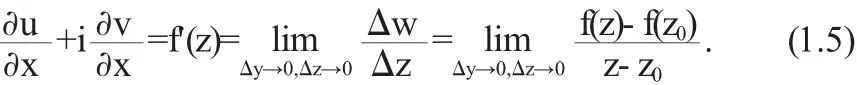
同理，設Δx=0,Δy→0，即點z+Δz沿著平于虛軸的方向趨于點z（圖1），此時(1.4)變為

由(1.5)，(1.6)及復數相等性質可得

則(1.7)稱為柯西－黎曼條件或柯西－黎曼方程，簡稱為方程.

總結上述討論，即得：

1.3 復變函數可微性的必要條件

設函數f(z)=u(x,y)+iv(x,y)在區域D內有定義，且在D內一點z=x+iy可微，則有

(1)在點(x,y)處偏導數ux，uy，vx，vy都存在；

(2)u(x,y)，v(x,y)在點(x,y)滿足C-R方程.

但它的逆命題不成立.

1.4 復變函數可微性的充分條件

設f(z)=u(x,y)+iv(x,y)在區域D內有定義，且f(z)在D內一點z=x+iy可微的充分條件是：

(1)偏導數ux，uy，vx，vy在點(x,y)處連續；

(2)u(x,y)，v(x,y)在點(x,y)滿足C-R方程.

1.5 復變函數可微性的充要條件

設f(z)=u(x,y)+iv(x,y)在區域D內有定義，則f(z)在D內一點z=x+iy可微的充要條件是：

(1)u(x,y)，v(x,y)在點(x,y)可微；

(2)u(x,y)，v(x,y)在點(x,y)滿足C-R方程．

當上述條件滿足時，有

例1證明函數f(z)=■|xy|在z=0有定義，但在z=0不可微.

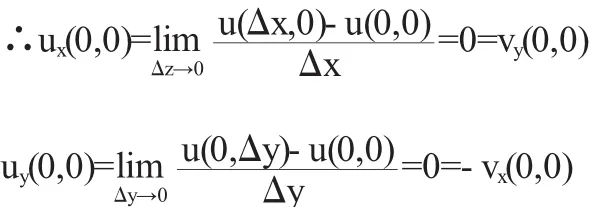
但是由于

因此當Δz沿著射線Δy=kΔx(Δx＞0)隨著Δx→0時，

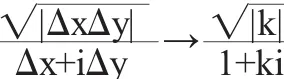
它是一個與k有關的值，故不存在，即f(z)在z=0不可微.

2 復變函數的解析性

2.1 復變函數解析性的定義

若函數w=f(z)在區域D內可微，則稱f(z)為區域D內的解析函數（或全純函數、正則函數）.此時也稱f(z)在區域D內解析.

解析函數是復變函數論研究的主要對象，它與相伴區域密切相關.以后說到f(z)在某點解析.則表示f(z)在該點的某一鄰域內解析，說f(z)在閉域D上解析，則表示f(z)在包含D的某個區域內解析．因而解析的概念要比可微的概念條件要強得多.

2.2 解析函數及其簡單性質

與數學分析一樣，解析函數也有如下基本性質：

(1)若f1(z),f2(z)在區域D內解析，則其和、差、積、商（在商的情形，要求分母在D內不為零）也在D內解析，且

(2)（復合函數求導法則）設ξ=f(z)在區域D內解析，w=g (ξ)在區域G內解析，若?z∈D均有ξ=f(z)∈G，則w=g[f(ξ)]在D內解析，且

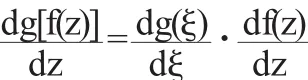
2.3 復變函數解析性的充要條件

函數f(z)=u(x,y)+iv(x,y)在區域D內解析的充要條件是：

(1)二元函數u(x,y)，v(x,y)在區域D內可微；

(2)u(x,y)，v(x,y)在區域D內滿足C-R方程.

2.4 復變函數解析性的充分條件

函數f(z)=u(x,y)+iv(x,y)在區域D內解析的充分條件是：

(1)ux，uy，vx，vy在區域D內連續；

(2)u(x,y)，v(x,y)在區域D內滿足C-R方程.

例2試證f(z)=ex(cosy+isiny)在z平面上處處解析，且f' (z)=f(z)

證明由已知u(x,y)=excosy,v(x,y)=exsiny可分別求它們的偏導數得

則滿足C-R方程.所以u(x,y),v(x,y)在z平面上處處可微，故由解析的充要條件f(z)在z平面上處處解析.且由公式(1.8)可得

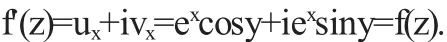
3 復變函數的可微性與解析性的區別與聯系

通過上述關于復變函數可微性與解析性的概念及它們成立的條件我們可以總結出它們之間的聯系：

(1)復變函數的解析性與可微性都滿足C-R方程；

(2)函數的可微性是函數解析的前提.

同時，它們之間還存在著區別：

(1)函數的可微性定義域可以是點也可以是區域，而函數的解析性定義域是只能是區域.

(2)函數f(z)在一點解析是針對一個局部鄰域，而函數在一點可微是對一個點而言.

所以可以總結出以下幾點是成立的：

(1)w=f(z)在點z0處可導(可微)，但不一定在z0處是解析的，

(2)f(z)在區域D內可微與在區域D內解析是等價的，

(3)函數f(z)在一點解析，則函數在該點一定可微.

例3函數f(z)=sinxchy+icosxshy何處可微？何處解析？

解由f(z)=sinxchy+icosxshy

設u(x,y)=sinxchy，v(x,y)=cosxshy可得它們對x和y的偏導數為

所以，函數在z平面上處處連續，且在整個復平面滿足C-R方程，故

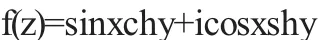
在z平面上處處可微，在z平面上處處不解析.

〔1〕鐘玉泉.復變函數(第三版)[M].北京：高等教育出版社，2004．

〔2〕鐘玉泉.復變函數學習指導書[M].北京：高等教育出版社，2003．

〔3〕余家榮.復變函數(第三版)[M].北京：高等教育出版社，2000．

〔4〕龔東寶.復變函數典型題解[M].西安：西安交通大學出版社，2002．

〔5〕路可見，等.復變函數[M].武漢：武漢大學出版社，2004．

〔6〕方企勤.復變函數教程[M].北京：北京大學出版社，1996．

O174

A

1673-260X（2013）08-0008-03