無刷直流電機反電動勢估計方法

劉棟良 崔言飛 陳鎂斌

（1.杭州電子科技大學自動化學院 杭州 310018 2.臥龍電氣集團有限公司 上虞 312300）

1 引言

無刷直流電機具有結構簡單、控制方便、可靠性高、功率密度大、效率高等優點，在工業領域得到廣泛應用。近年來，無刷直流電機的無位置傳感器控制一直是國內外的研究熱點，較為常見的轉子位置信號檢測方法有[1-7]：①反電動勢法，它是目前技術相對成熟，實現比較簡單，但缺點是靜止或低速時反電動勢信號很小，難以得到有效的轉子位置，系統低速性能比較差；②定子電感法，它利用電機繞組電感和轉子位置的一定對應關系，通過重構的中性點電位代表位置信息，因此低速性能有所提高，但這種方法需要對繞組電感進行實時檢測，增加了實現的難度。另外，如續流二極管法、磁鏈估計法和狀態觀測器法等，不同程度上改善了低速性能，但增加了控制難度，系統的動靜態特性都不夠理想，其限制了直流無刷電機的應用。文獻[8]在低速和高速時，分別在PWM 關斷和開通階段檢測反電動勢，采用2 個不同的參考電壓獲得反電動勢過零點，它不需位置傳感器和電流傳感器，但增加了硬件電路的復雜性。文獻[9]通過比較懸空相繞組端電壓和逆變器直流環中點電壓的關系，獲得反電動勢過零點，該方法無需重構電機中性點，不使用濾波電路，但仍需采用硬件電路比較得到過零點。文獻[10]提出了一種基于繞組電感與轉子位置的關系，解決無刷直流電機中低速無傳感器運行的問題，但該方法具有很大的滯后性，實時性較差。

因此本文提出了一種基于卡爾曼濾波方法的無刷直流電機的反電動勢檢測改良新方法，該方法將相電流和反電動勢作為狀態變量，在無刷直流電機數學模型的基礎上進行推導，得到卡爾曼濾波模型。該算法不需要任何額外的檢測電路，具有實現穩態和瞬態準確換向，能對電機轉速進行精確控制，在很大程度上克服了直接反電動勢法的抗干擾能力差、計算延遲和低通濾波相移等問題。

2 反電動勢檢測基本原理

普通無刷直流電機采用三相電壓型逆變器供電，其定子繞組為星形聯結，如圖1 所示。由于無刷直流電機中點n 一般不引出，所以很難準確構建相電壓方程[7-9]，為此考慮構建線電壓方程，將上述三相相電壓兩兩相減即可得到線電壓表達式[5,7]為

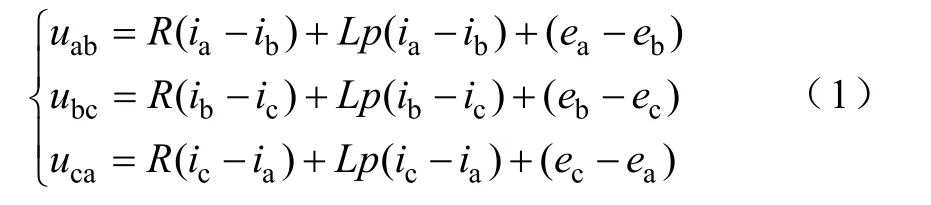
式中p——微分算子，d/(dt)；

R——定子電阻；

L=LS?M；

Ls——定子相繞組自感；

M——定子相繞組互感。

圖1 三相無刷直流電機主電路圖Fig.1 Three-phase brushless DC circuit diagram

進一步考慮線電壓的差值，以uab與ubc為例，將uab與ubc相減得到

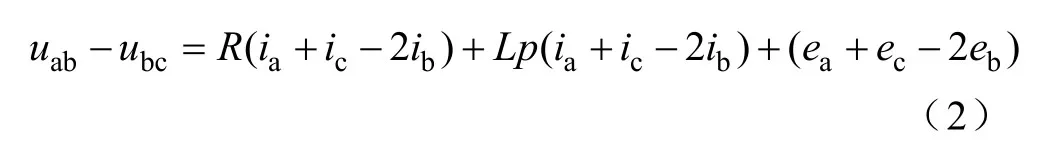
假設a 相和c 相導通，b 相不導通，則ea+ec=0（理想反電動勢和電流曲線見圖2），而由無刷直流電機三相定子繞組星形聯結可知：ia+ib+ic=0，則式（2）可以簡化為

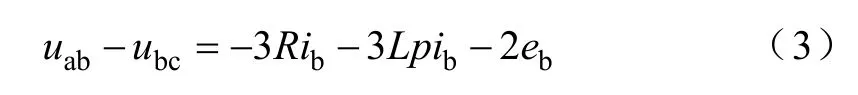
即

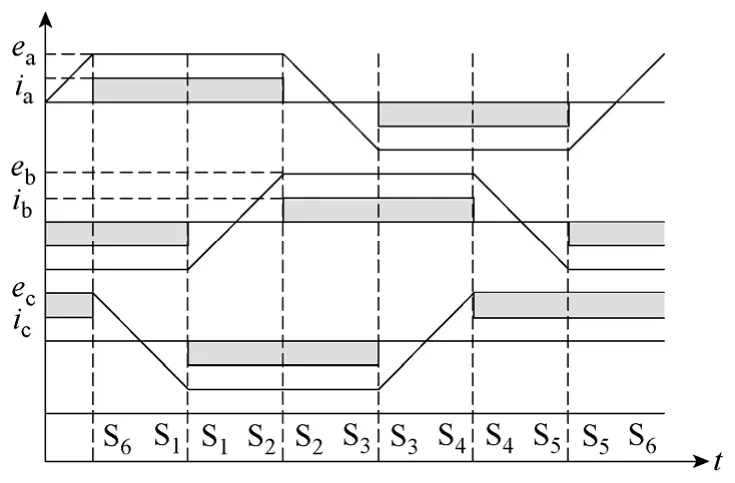
圖2 理想反電動勢、電流波形Fig.2 Ideal back-EMF voltage and current waveform

3 擴展卡爾曼濾波器原理

卡爾曼濾波方法是系統噪聲正態分布時，這種濾波給出了狀態的最小方差估計，當不是正態情況時，這種濾波給出了狀態的線性最小方差估計。卡爾曼濾波是在線性基礎上發展起來的，然而實際系統往往都不是線性的。電機系統就是一個非線性系統，對于非線性系統問題的應用關鍵是非線性方程的線性化問題。在此基礎上關于離散線性系統的卡爾曼濾波估計公式可以推廣應用于連續的非線性系統[11]。設非線性微分方程為

式中，x為系統的狀態矢量；U為系統的干擾函數矢量。

則兩個雅克比矩陣分別為

即線性干擾方程[11-14]。具有初始條件x(t0)=x0時，線性非齊次微分方程的解是

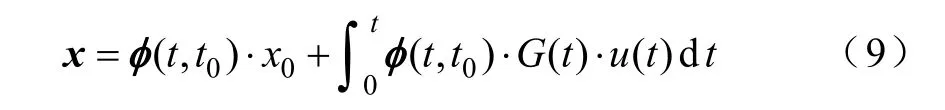
狀態轉移矩陣φ(t,t0)是 dφ(t,t0)/(dt)=F(t)·φ(t,t0)的解。初始條件G(t)dt，則式（9）可寫成如下差分方程形式

測量方程線性化，設

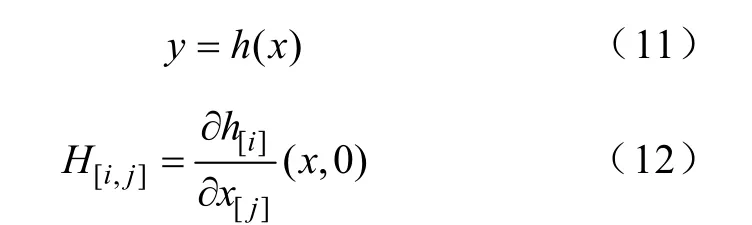
則式（11）寫成

顯然在式（8）和式（13）中附加白噪聲序列Wk-1和Vk，便完成了卡爾曼濾波器的非線性化問題[11-14]。

以下是構造擴展卡爾曼濾波器的一般步驟[10,11]:（1）計算狀態預報值

（2）狀態誤差協方差矩陣

（3）卡爾曼濾波器增益

式中，Rk為噪聲協方差；K(k+1)是tk+1=(k+1)T時刻的卡爾曼濾波器增益。

（4）狀態誤差協方差矩陣的更新

式中，1ky+是 1kt+時刻觀測方程的測量值。

（5）狀態預報值更新

式中，1ky+是 1kt+時刻觀測方程的測量值。

4 利用卡爾曼濾波器進行反電動勢估計

由于式（4）中ib、ubc和uab可以測量，這里作為已知狀態變量；由于eb不可以直接測量，作為未知狀態變量。則式（4）可以寫成

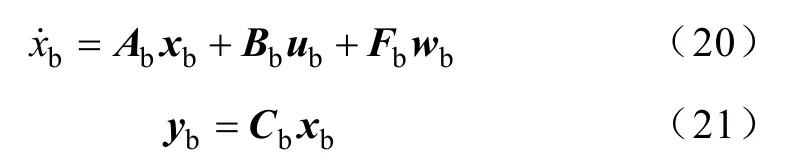
式中

上式中將反電動勢看作未知的擾動信號，而這個擾動信號可以由以下差分方程來描述

式中，I是單位矩陣；δ是多項式w的次數，且δ≥1；ai是未知矢量的系數。

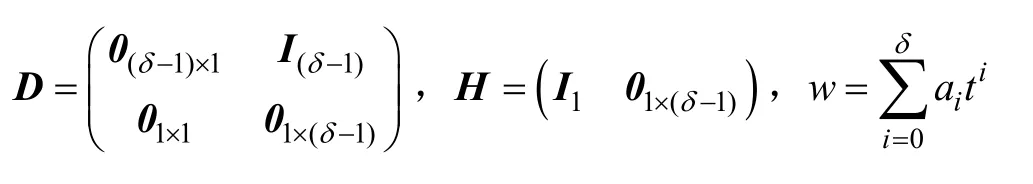
當沒有擾動時，可令ai=0。以上的方法通過改變多項式的次數可以描述大多數的擾動信號和一些未知擾動信號，因此，不失一般性，在動態系統中擾動模型式（22）和式（23）是完全可觀的[12]，所以，反電動勢方程可由引入擾動的差分方程來描述

式中

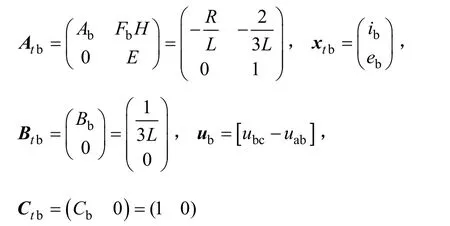
同理，可得其他兩相的狀態模型，最終可得系統狀態模型

式中x=（iaeaibebicec）T；

式（26）和式（27）中附加白噪聲序列Wk-1和Vk，便完成了無刷直流電機反電動勢檢測的卡爾曼濾波非線性化問題。

利用第3 小節所述方法進行迭代運算，便可得到電機運行時的反電動勢值，當相電流接近零，且反電動勢為零時進行換向，便可對電機進行控制。

5 速度和位置計算

以上利用卡爾曼濾波器可以估計出各相反電動勢的大小，這里利用估計出的反電動勢的值，通過簡單的計算可估計出電機的速度和位置[15-18]，具體如下：

式中E——反電動勢的幅值；

Ke——反電動勢常數；

ωe——電機的電角速度，ωe=E/Ke。

進而可得到電機的轉子位置

式中θ——轉子位置角；

θ0——轉子初始位置角。

6 實驗驗證

基于擴展卡爾曼濾波的反電動勢估計無刷直流電機速度控制系統框圖如圖3 所示，圖中ωm=2ωe/p，式中，ωm為電機的機械角速度；p為電機的磁極對數。

圖3 系統控制結構框圖Fig.3 The framework diagram of the control system

根據系統控制框圖構建其實驗平臺，整個控制平臺以TI 公司的TMS320VC33 DSP 芯片為核心，以三菱智能IPM 為驅動模塊組成的BLDC 拖動控制實驗平臺。其中圖4 為實驗控制系統，無刷直流電機主要參數為：額定電壓310V，額定轉矩15Nm，額定轉速1 000r/min，極對數為2 極，反電動勢常數是0.175，定子電阻1.5Ω，定子電感4.22mH。

圖4 BLDC 控制實驗平臺Fig.4 The experiment flatform of BLDC

系統實驗分三個部分：

（1）當0～1s 給定線性轉速到1 000r/min，空載時結果如圖5 所示。

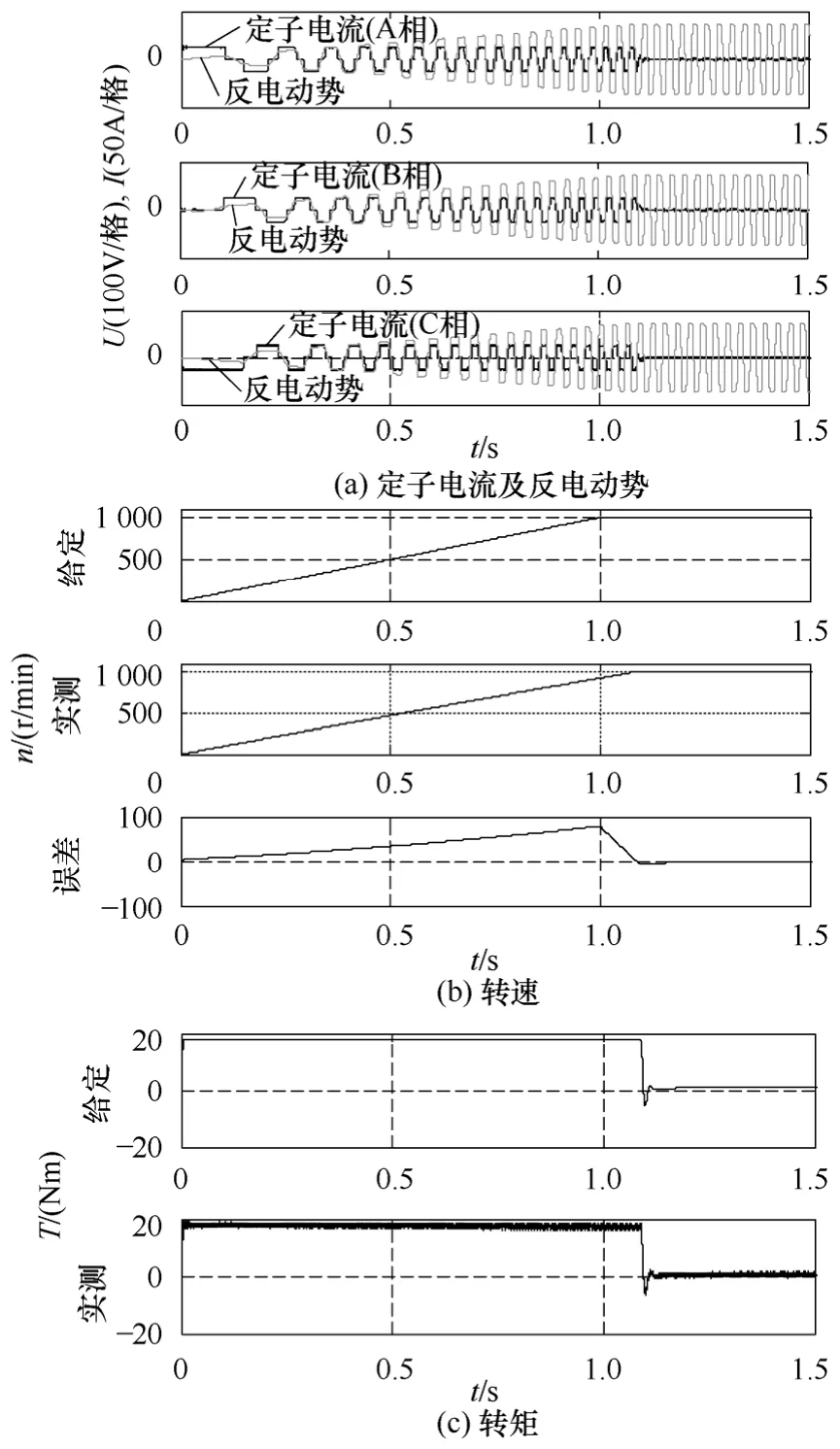
圖5 空載時無刷直流電機對應波形Fig.5 The wave of BLDC for no load

從圖5a 可以看出理想的反電動勢和電流曲線非常接近，實現了當相電流接近為零和反電動勢過零檢測，無明顯的續流現象。從圖5b 可以看出在電機起動瞬間速度跟蹤的偏差近似呈線性增加當達到1s 時迅速下降，并帶有小量的超調現象，過渡過程大概0.1s，隨后進入穩態，穩態時無偏差。圖5c 描述了轉矩跟蹤情況，從圖中可以看出轉矩的跟蹤情況較好，無明顯偏差。

（2）當0～1s 給定線性轉速到1 000r/min，2s突加15Nm 轉矩時結果如圖6 所示。

圖6 突加負載時無刷直流電機對應波形Fig.6 The wave of BLDC for impact load

由圖6a 可以看出理想的反電動勢和電流曲線非常接近，實現了當相電流接近為零和反電動勢過零檢測，無明顯的續流現象；開始隨著轉速的增加，電流和反電動勢均隨之增加，當1.1s 達到給定轉速時電流和反電動勢基本不變；當2s 時轉矩突變，電流和反電動勢又隨之增大經過0.2s的時間又進入另 外一個穩態。圖6b 中看出系統啟動時隨著速度的增加，轉速偏差也近似地呈線性增加，當時間達到1s時轉速偏差達到最大值 80r/min，隨后偏差迅速減小。隨著轉速的增大，伴隨有少量的超調現象，但是過渡過程很短，大概0.2s的時間，隨后進入穩態；當2s 時突加15Nm 轉矩時，轉速有少許的降落，經過0.2s的調整時間進入穩態。圖6c 中可以看出實際的輸出轉矩可以很好地跟蹤給定轉矩。

（3）當0～1s 給定線性轉速為1 000r/min，2s時突加15Nm 轉矩，3s 給定線性轉速到50r/min 時結果如圖7 所示。

由圖7a 中可以看出理想的反電動勢和電流曲線非常接近，實現了當相電流接近為零和反電動勢過零檢測，無明顯的續流現象；開始隨著轉速的增加電流和反電動勢均隨之增加，當1.2s 時達到給定轉速，電流和反電動勢基本不變，當2s 時轉矩突變，電流和反電動勢又隨之增大經過0.2s的時間又進入 另外一個穩態；當3s 時給定轉速給定下降，電流和反電動勢迅速減小，經過短暫的過度過程進入穩態；當3.8s 時轉矩突然反向，這時電流也迅速改變方向，經過大概0.4s的過渡時間進入穩態。圖7b 中看出系統啟動時隨著速度的增大，轉速偏差也隨之增大，當時間達到1s 時速度偏差達到最大值，隨后偏差迅速減小，在1.2s的時候進入穩態；當時間到達2s時由于外加轉矩突變產生了轉速降落，經過0.3s的時間才進入穩態，不過轉速降落的幅度很小；當時間到達3s 時，轉速指令由1 000r/min 變成50r/min，變化瞬間轉速有少量的偏差，0.2s 后就可以很好的跟蹤給定轉速；在3.8s 時由于轉矩的突變，轉速瞬間出現了降落，經0.3s的時間進入穩態。從圖7c可以看出實際的輸出轉矩可以很好地跟蹤給定轉矩。

7 結論

本文針對傳統直流無刷電機無位置傳感器檢測方法過于復雜、實時性差，提出了一種基于卡爾曼濾波器的無刷直流電機反電動勢過零檢測改良新方法，并在TI 公司的DSP 芯片為核心的實驗平臺上進行了實驗驗證。理論和實驗結果表明該算法的可行性，并且該算法簡單，無需復雜電路檢測，能進行準確的換向，使電機轉速精確控制，具有較高的應用價值。

[1]宋海龍,楊明,范宇,等.無刷直流電動機的無位置傳感器控制[J].電機與控制學報,2002,6(3):208-212.Song Hailong,Yang Ming,Fan Yu,et al.Review of sensorless control of brushless DC motor[J].Electric Machines and Control,2002,6(3):208-212.

[2]周艷青,尹華杰,葉長青.無位置傳感器無刷直流電機位置檢測技術[J].電機與控制應用,2007,34(7):1-5.Zhou Yanqing,Yin Huajie,Ye Changqing.Position detection for position sensorless brushless DC motor[J].Electric Machines & Control Application,2007,34(7):1-5.

[3]Kim T H,Ehasani M.Sensorless control of the BLDC motors from near-zero to high speeds[J].IEEE Trans.on Power Electronics,2004,19(6):1635-1645.

[4]Shao Jianwen,Dennis Nolan.A novel direct back EMF detection for sensorless brushless DC(BLDC)motor drives[C].17th Annual IEEE Conference and Exposition on Applied Power Electronics,2002,1:33-37.

[5]張磊,瞿文龍,陸海峰,等.一種新穎的無刷直流電機無位置傳感器控制系統[J].電工技術學報,2006,21(10):26-30.Zhang Lei,Qu Wenlong,Lu Haifeng,et al.A novel sensorless control system of brushless DC motors[J].Transactions of China Electrotechnical Society,2006,21(10):26-30.

[6]王宏偉,梁暉.無位置傳感器無刷直流電機的DSP控制[J].電力電子技術,2005,39(6):102-104.Wang Hongwei,Liang Hui.DSP control of brushless DC motor without position sensor[J].Power Electronics,2005,39(6):102-104.

[7]Shao Jianwen.An improved microcontroller-based sensorless brushless DC(BLDC)motor driver for automotive applications[J].IEEE Transactions on Industry Applications,2006,42(5):1216-1221.

[8]李志強,夏長亮,陳煒.基于線反電動勢的無刷直流電機無位置傳感器控制[J].電工技術學報,2010,25(7):38-44.Li Zhiqiang Xia Changliang Chen Wei.A position sensorless control strategy for BLDCM based on line back-EMF[J].Transactions of China Electrotechnical Society,2010,25(7):38-44.

[9]Jiang Quan,Bi Chao.A new phase-delay-free method to detect back EMF zero-crossing points for sensorless control of spindle motros[J].IEEE Transactions on Magnetics,2005,41(7):2287-2294.

[10]王華斌,劉和平,張毅,等.計及中性點電壓的無刷直流電機無位置傳感器控制[J].電工技術學報,2009,24(7):46-51.Wang Huabin,Liu Heping,Zhang Yi,et al.Sensorless BLDC drive allowing for neutral point voltage[J].Transactions of China Electrotechnical Society,2009,24(7):46-51.

[11]敬喜.卡爾曼濾波器極其應用基礎[M].北京:國防工業出版社,1973.

[12]Tae Sung Kim,et al.A new approach to sensorless control method for brushless DC motors[J].International Journal of Control,Automation,and Systems,2008,6(4):477-487.

[13]Gunabalan R,et al.Sensorless control of induction motor with extended Kalman filter on TMS320F2812 processor[J].International Journal of Recent Trends in Engineering,2009,2(5):14-19.

[14]林海,嚴衛生,林洋,等.雙擴展卡爾曼濾波的無刷直流電機無傳感器控制[J].西北工業大學學報,2010,28(2):197-201.Lin Hai,YanWeisheng,Lin Yang,et al.Applying dual extended Kalman filter(DEKF)theory to sensorless control of brushless DC motor(BLDCM)[J].Journal of Northwestern Poly Technical University,2010,28(2):197-201.

[15]Jang G H,Kim M G.Optimal commutation of a BLDC motor by utilizing the symmetric terminal voltage[J].IEEE Transactions on Magnetics,2006,42(10):3473-3475.

[16]鄒繼斌,江善林,張洪亮.一種新型的無位置傳感器無刷直流電機轉子位置檢測方法[J].電工技術學報,2009,24(4):48-53.Zou Jibin,Jiang Shanlin,Zhang Hongliang.A novel method of detecting for rotor position of a sensorless brushless DC motor[J].Transactions of China Electrotechnical Society,2009,24(4):48-53.

[17]吳小婧,周波,宋飛.基于端電壓對稱的無位置傳感器無刷直流電機位置信號相位校正[J].電工技術學報,2009,24(4):54-59.Wu Xiaojing,Zhou Bo,Song Fei.A new control method to correct position phase for sensorless brushless DC motor[J].Transactions of China Electrotechnical Society,2009,24(4):54-59.

[18]Yen Shin Lai,Fu Shan Shyu.Novel back-EMF detection technique of brushless DC motor drives for whole duty-ratio range control[C].The 30th Annual Conference of the IEEE Industrial Electronics Society,Busan,Korea,2004,3:2729-2732.