地鐵牽引變流器-電機系統穩定性控制

趙雷廷 刁利軍 董 侃 劉志剛

(北京交通大學電氣工程學院 北京 100044)

1 引言

牽引變流器-電機系統是地鐵車輛的動力來源，由直流接觸網、濾波器（濾波電感與支撐電容）、牽引變流器、牽引電機等組成[1,2]。鑒于運營的實際需求，多車輛同時啟動或者制動的情況時有發生，而且隨著近年來四象限變流器等吸收裝置在供電系統中的引入[3]，一旦供電系統控制參數設計與當前實際運營數據不匹配，則很容易引起直流網側電壓波動；與此同時，直流側濾波電感及支撐電容受到車載變流裝置本身空間、重量以及諧波抑制要求等諸多因素限制，參數的選擇通常為較大的電感、較小的電容，且為了避免能量的過多損耗，線路電阻與電感內阻之和也不宜設計過大，因此系統阻尼系數較小[4]；而牽引變流器在矢量控制策略下呈現負阻抗特性[5]，導致系統阻尼系數再次減小，從而引發牽引傳動系統直流側電壓、電流持續振蕩，電機輸出轉矩脈動，嚴重時則會產生過壓、過流故障保護，牽引變流器封鎖脈沖，系統喪失牽引力。

為確保地鐵車輛的安全穩定運行，“輸入濾波器-牽引變流器-異步電機”的整體系統穩定性研究已經逐漸成為業界研究的重要方向之一，SIEMENS、Bombardier、ALSTOM 等國外廠商針對上述問題已經展開了細致的分析并提出了一些相關的解決措施[6-8]，這些措施都以完美的轉矩控制為前提，在系統運行的某一工作點附近利用小信號分析法將牽引變流器等效為一個恒定的阻抗[9]，然而牽引傳動系統在實際的運行過程中，由于受到磁鏈觀測誤差、A-D 采樣誤差、諧波干擾以及系統時延等因素的影響，完美的轉矩控制是不可能真正實現的，因此恒定的阻抗并不能用來準確且全面地分析系統的穩定性[10]。

本文通過建立牽引傳動系統線性化結構圖、異步電機Γ形等效電路以及轉子磁場定向矢量控制近似線性化模型，從而得到牽引變流器輸入導納線性化模型，在此基礎上針對整個系統的穩定性進行分析，闡釋系統的振蕩機理并提出一種新型穩定性控制器以獲得理想的牽引變流器輸入導納，從而抑制系統振蕩，提高系統穩定性。

2 牽引傳動系統結構

圖1 所示為地鐵牽引傳動系統框圖。直流接觸網通過輸入濾波器向牽引變流器提供 1 500V 或750V 直流電，轉矩控制系統采集直流側電壓Ud、電機定子三相電流ia、ib、ic以及電機機械轉速ωm，采用轉子磁場定向矢量控制，輸出三相變頻變壓交流電以驅動異步電機運行。

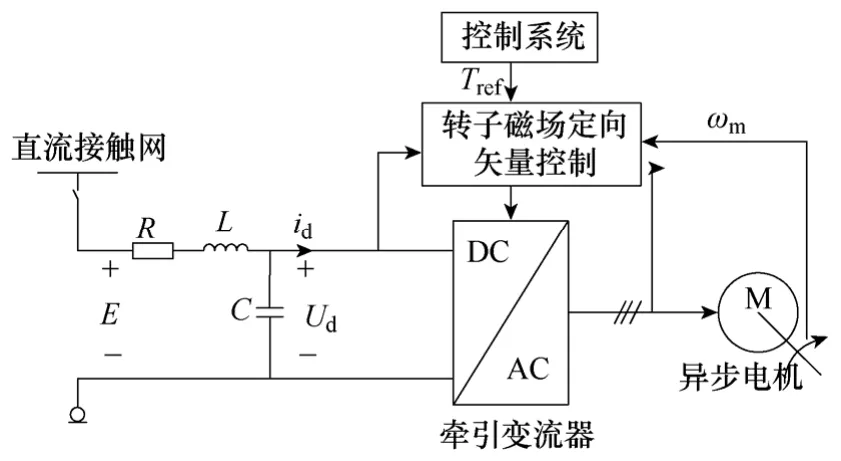
圖1 地鐵牽引傳動系統框圖Fig.1 Schematic of metro drive system

圖1 中，R為線路電阻與電感內阻之和，L為濾波電感，C為支撐電容。系統直流側電壓通過牽引變流器影響直流側電流，在完美的轉矩控制前提下牽引變流器可以被等效為一恒定阻抗，而本文基于實際的運行情況將牽引變流器等效為一非線性函數

從而定義牽引變流器線性化輸入導納為

如果將直流網側電壓與直流側電流作為牽引傳動系統的輸入，直流側電壓作為系統輸出，則系統輸入濾波器頻域下方程為

結合式（2）最終可以得到牽引傳動系統線性化結構圖如圖2 所示，繼而將系統穩定性的分析歸結于對牽引變流器線性化導納模型的分析。

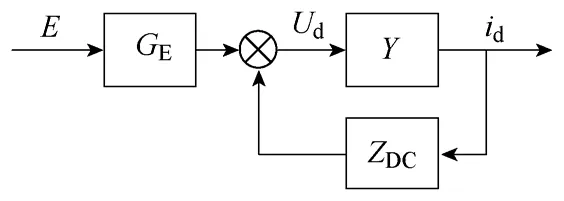
圖2 牽引傳動系統線性化結構圖Fig.2 Linear feedback model of drive system

3 系統穩定性分析

3.1 牽引變流器線性化導納模型建立

這里通過建立異步電機數學等效模型、變流器脈寬調制策略以及轉子磁場定向矢量控制的近似線性化模型，最終得到牽引變流器輸入導納線性化模型。結合上文所述系統直流側濾波器模型，對牽引傳動系統的整體穩定性進行分析。

建立圖3 所示考慮漏感的異步電機Γ形等效電路圖，其特點是定子漏感為0，LM=Ls即等效勵磁磁鏈ψM等于實際的定子磁鏈ψs[11]。Rs和RR分別為電機定子電阻和等效轉子電阻，Lσ則表示電機等效漏感，rψ′為轉子磁鏈。

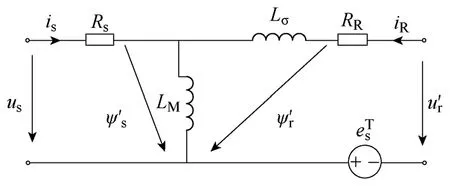
圖3 異步電機Γ形等效電路Fig.3 Γ-equivalent circuit of induction motor

根據Γ形等效電路建立異步電機在同步旋轉坐標系下采用轉子磁場定向矢量控制的數學模型

式中

同時牽引變流器采用PWM 脈寬調制策略，在當前開關周期內將直流電壓轉變為與控制系統給定電壓值相等的可變頻變壓三相電機定子交流電壓以驅動異步電機運行，電機定子電壓us模型如下所示

為補償直流側電壓波動的影響，表征PWM 脈寬調制策略等效函數的k(t)被定義為

式中，usref為控制系統給定電機定子電壓值；Ud上標橫線表示其在一個開關周期內的平均值。

通過使用小信號模型分析法將式（8）線性化，可得

下標0 表示對應變量穩態值，A(t)為開關周期內求解平均值函數，結合式（7）最終可獲得電機定子電壓線性化模型為

為消除異步電機等效模型由靜止坐標系轉換到旋轉坐標系時所產生的耦合分量jωeLσ，控制系統采用反饋解耦策略[12]，將電流控制器與異步電機模型所建立的開環傳遞函數開環極點在旋轉坐標系下從-R/Lσ-jωe轉移到-R/Lσ，進而通過選擇適當的電流控制器PI 參數實現零極點對消，提高系統動態響應，最終使電流控制的特性獨立于同步頻率的變化。與此同時考慮到異步電機反饋電動勢的存在，增加主動阻尼系數Ra以提高系統的抗干擾能力[13]，電流控制器與異步電機系統結構圖如圖4 所示。

圖4 電流PI 控制器與異步電機系統結構圖Fig.4 Representation of the induction motor with PI current regulation

根據圖4，電機定子電壓給定值的表達式如下

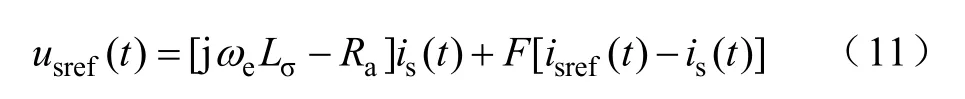
式中

將反饋解耦以及主動阻尼系數與異步電機模型合并，得到電機定子電流轉矩分量閉環控制系統框圖如圖5 所示。

圖5 電流轉矩分量閉環控制系統Fig.5 Closed-loop control system of quadrature current

從而得到基于轉子磁場定向控制的牽引傳動系統近似線性化模型

綜合式（4）和式（5）建立輸入濾波器-牽引變流器-異步電機的綜合線性化模型如圖6a 所示，電機定子電流轉矩分量給定值和網側電壓作為系統輸入，電機輸出轉矩以及直流側電流作為系統輸出。圖中陰影部分形成的反饋回路在實際運行過程中即使在系統內部轉矩控制良好的情況下也會產生不穩定現象。為簡化反饋回路結構，引入上文所述牽引變流器輸入導納，得到圖6b。

圖6 系統綜合線性化模型Fig.6 Comprehensive linear model of drive system

根據圖6b 最終得到牽引變流器輸入導納線性化模型以及電機輸出轉矩、直流側電壓、電流線性化表達式如下所示

3.2 直流側振蕩產生機理

在傳遞函數GC、Gd以及變流器輸入線性化導納Y自身穩定的前提下，牽引傳動系統整體穩定性取決于開環傳遞函數YZDC。由于系統輸入濾波器ZDC阻尼系數較小，因此在諧振頻率ω0附近其對數幅頻曲線有較大的尖峰，同時相角從90°突變至-90°，如果此時線性化輸入導納Y等效為復頻域下一向量，當 Re{Y(ω0)}＜0 時，arg(YZDC(ω))必然穿越(2k+1)180°（k=0、±1、±2…），如圖7 所示。

圖7 開環傳遞函數YZDC Bode 圖Fig.7 Bode diagram of open-loop transfer function YZDC

圖7 為系統在直流側電壓1500V，濾波電感5.2mH，支撐電容 8.6mF，線路電阻與電感內阻之和34.8mΩ，電機等效漏感2mH，額定勵磁電流60A條件下的開環傳遞函數YZDC頻率域穩定分析仿真結果，在幅頻特性曲線大于0的頻率范圍之內相頻特性曲線穿越180°一次，根據奈奎斯特對數頻率穩定判據可知此時系統處于不穩定狀態，整個系統將產生持續振蕩。

為抑制系統振蕩，提高穩定性，則需要線性化導納在復頻域下相角始終處于90°到-90°之間，至少在輸入濾波器諧振頻率附近滿足上述條件，因此如何獲得理想的變流器輸入導納成為了系統穩定性設計的關鍵。

4 系統穩定性控制器設計

由于系統穩定性依賴于理想變流器輸入導納線性化模型。因此本文通過設計穩定性控制器在線修正電機定子電流轉矩分量給定值，以獲得最終的理想導納模型，修正公式如下：

式中，KSC為穩定性控制器。

結合式（14）可以得到

在(1-A(s))≈sTa的條件下，Ta為開關周期內平均值傳遞函數等效時間，則式（18）轉化為

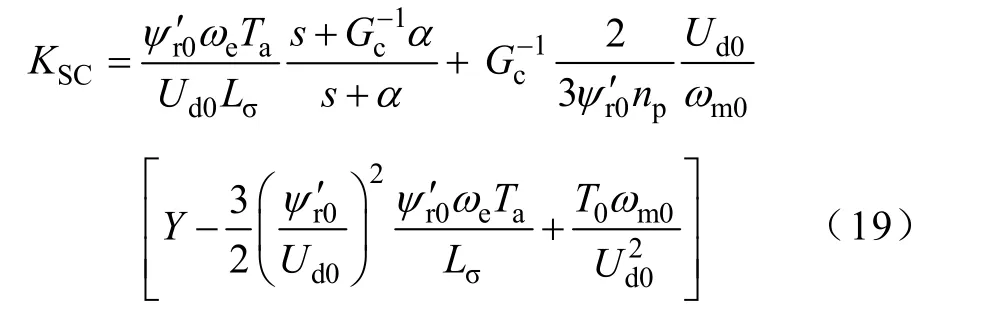
為使系統穩定并且具有最大的穩定裕度，理想的變流器輸入導納線性化模型在復頻域下應為一具有正實部且虛部為0的矢量[14]為

在牽引變流器等效為上述理想線性化輸入導納的條件下，整個牽引傳動系統Bode 圖如圖8 所示。

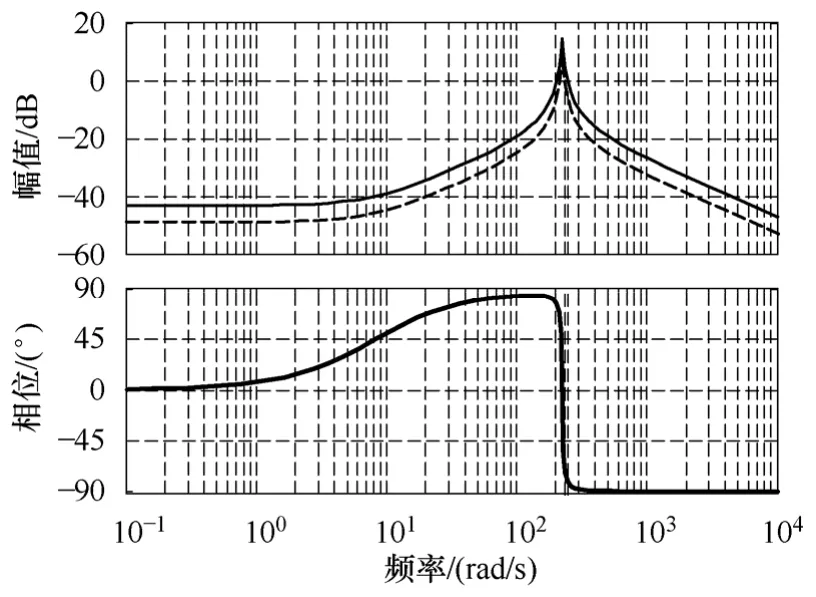
圖8 理想線性化輸入導納下的開環 傳遞函數YdZDC Bode 圖Fig.8 Bode diagram of open-loop transfer function YdZDC with ideal linear input admittance model

圖8 中實線與虛線分別為系統在牽引工況以及制動工況下的對數幅相曲線，與圖7 相比，理想變流器輸入導納線性化模型使系統開環傳遞函數YdZDC在車輛運行的任何工況下其相角都維持在 90°～-90°之間，從而使得系統處于穩定狀態。

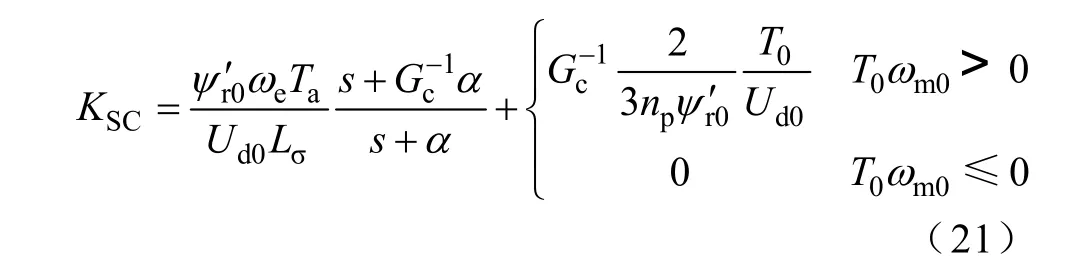
將理想變流器輸入導納線性化模型代入式（19）得 用濾波器Fl[6]代替式（21）第二項中的，同時將

為獲得穩定性控制器KSC的精確數學模型，使 第一項中的近似等于 0.5，損失一定的穩定裕 度，以降低直流側電壓波動對電機輸出轉矩的影響，因此可以得到穩定性控制器最終模型為

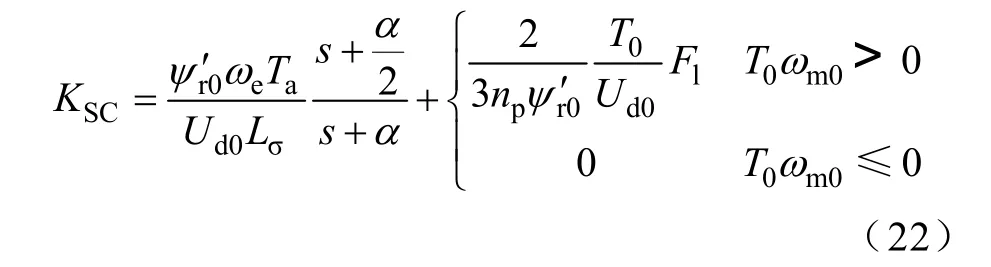
圖9 給出了采用穩定性控制器與未采用穩定性控制器牽引傳動系統運行時主要變量的仿真波形對比。其中包括電機轉速n、電機輸出轉矩T、直流側電壓Ud以及網側直流電流ig。

圖9 牽引傳動系統運行仿真圖Fig.9 Simulation of drive system

從對比中可以看出系統采用穩定性控制器之后，牽引變流器在電機轉速從0 上升至3 300r/min，運行工況由牽引→惰性→制動的過程中，消除了系統振蕩現象，直流側電壓、網側直流電流以及電機輸出轉矩變化平穩。

5 實驗驗證

圖10 所示為自主開發研制的地鐵A 型車牽引變流器。其直流側線路電壓1 500V，輸入電流500A，額定容量1 000kVA，輸出頻率0～112Hz。為驗證上述理論的正確性，本文進行了相關實驗。

圖10 地鐵牽引變流器實物圖Fig.10 Metro traction convertor

圖11 為系統未采用穩定性控制器時，車輛在牽引工況下加速過程中，變流器直流側以及電機振蕩的波形圖。其中包括同一變流器兩并聯電機交流側電流和ia、網側直流電流ig、直流側電壓Ud以及車速vp。從圖中可以看出，車輛在AW0 載荷下，電機首先運行于恒轉矩區，其輸出轉矩經過箱體溫度、車輛載荷、防滑/防空轉以及電機特性曲線等限制模塊之后最終基本維持在1 000Nm。隨著地鐵車輛的速度增加，牽引變流器輸出功率逐漸上升。當速度達到25km/h 左右，功率大約為220kW 時，牽引變流器直流側電壓、網側直流電流、交流側電流以及電機輸出電流都出現持續振蕩現象，直到車輛運行至30km/h 時，進入惰性工況。

圖11 牽引傳動系統直流側和電機側振蕩波形Fig.11 The oscillation of traction drive system on the traction condition

圖12 所示則為系統加入穩定性控制器之后，變流器直流側電壓，網側直流電流以及電機輸出電流波形圖。隨著車輛速度增加至25km/h 左右進入惰性工況，以及之后再次加速至55km/h的整個過程中，系統振蕩得到了抑制，地鐵車輛穩定運行。從而驗證了上文所述穩定性控制器的正確性和有效性。

圖12 牽引傳動系統穩定運行波形Fig.12 Stable operation of traction drive system

6 結論

本文將直流側輸入濾波器以及牽引變流器控制策略相結合，分析了地鐵牽引變流器-電機系統的整體穩定性。通過建立異步電機Γ 形等效電路以及轉子磁場定向矢量控制的近似線性化模型從而得到了變流器輸入導納線性化模型，利用奈奎斯特對數頻率穩定判據闡釋了系統振蕩的機理。在此基礎上提出了一種以獲得理想變流器輸入導納為目的的系統穩定性控制器，并給出其精確模型。模型仿真以及現場的實驗都證明了該控制器的正確性和有效性，成功解決了牽引傳動系統振蕩的問題，確保了地鐵車輛的安全穩定運行。

[1]孫大南.地鐵車輛牽引電傳動系統關鍵技術研究[D].北京:北京交通大學,2012.

[2]陳曉麗,何林娜.城市軌道交通車輛交流傳動系統建模與仿真分析[J].城市軌道交通研究,2011(10):33-36.Chen Xiaoli,He Linna.Modeling and simulation of AC traction system for urban railway vehicles[J].Urban Rail Transit Research,2011(10):33-36.

[3]孔嵩.地鐵能饋式牽引供電變流系統諧波分析及抑制研究[D].北京:北京交通大學,2011.

[4]Mosskull Henrik,Galic Johann,Wahlberg Bo.Stabilization of induction motor drives with poorly damped input filters[J].IEEE Transactions on Industrial Electronics,2007,54(5):2724-2734.

[5]Pietilainen Kai,Harnefors Lennart,Petersson Andreas,et al.DC-link stabilization and voltage sag ride-through of inverter drives[J].IEEE Transactions on Industrial Electronics,2006,53(4):1261-1268.

[6]Bae B H,Cho B H,Sul S K.Damping control strategy for the vector controlled traction drive[C].European Conference on Power Electronics and Applications,Graz,2001.

[7]Delemontey B,Iung C,Fornel B De,et al.Nonlinear decoupling of an induction motor drive with input filter[C].IEEE Conference on Control Applications,USA,1995:1004-1009.

[8]Delemontey B,Iung C,Fornel B De,et al.Stability analysis and stabilization of an induction motor drive with input filter[C].European Conference on Power Electronics and Applications,Spain,1995:2724-2734.

[9]孫大南,劉志剛,林文立,等.地鐵牽引變流器直流側振蕩抑制策略研究[J].鐵道學報,2011,33(8):52-57.Sun Danan,Liu Zhigang,Lin Wenli,et al.Research on DC-link oscillation suppression strategy in metro traction convertor[J].Journal of the China Railway Society,2011,33(8):52-57.

[10]Henrik Mosskull.Stabilization of an induction machine drive[D].Sweden:Royal Institute of Technology,2003.

[11]Lennart Harnefors,Kai Pietilainen,Lars Gertmar.Torque-maximizing field-weakening control:design,analysis,and parameter selection[J].IEEE Transactions on Industrial Electronics,2001,48(1):161-168.

[12]Fernando Briz,Michael W Degner,Robert D Lorenz.Analysis and design of current regulators using complex vectors[J].IEEE Transactions on Industry Applications,2000,36(3):817-825.

[13]Fernando Briz del Blanco,Michael W.Dynamic analysis of current regulators for AC motors using complex vectors[J].IEEE Transactions on Industrial Electronics,1999,35(6):1424-1432.

[14]Henrik Mosskull.Stabilization of an induction motor drive with resonant input filter[C].Power Electronics and Applications,2005:10pp.-p.10.