基于局部線性嵌入和云神經(jīng)網(wǎng)絡(luò)的轉(zhuǎn)子故障診斷方法

孫 斌，薛廣鑫，陳 軍，蔣能飛

(東北電力大學(xué) 能源與動力工程學(xué)院，吉林 132012)

從大量的振動數(shù)據(jù)中找出有效的特征信息是汽輪機運行狀態(tài)在線監(jiān)測和故障診斷的一個重要環(huán)節(jié)，故障特征提取關(guān)系診斷結(jié)果的準(zhǔn)確程度。傳統(tǒng)的轉(zhuǎn)子狀態(tài)監(jiān)測和故障診斷方法主要是基于傅里葉變換和小波變換理論，傅里葉變換能夠計算出信號時域或頻域特征參數(shù)的統(tǒng)計結(jié)果，卻無法同時兼顧時域和頻域的全貌和局部化特征。小波變換在傅里葉變換的基礎(chǔ)上增加了可調(diào)窗口的功能，被稱為“數(shù)學(xué)顯微鏡”，然而小波基函數(shù)的長度有限，在變換過程中會產(chǎn)生能量泄露，小波基函數(shù)和分解尺度限制了分析頻率的范圍，缺乏自適應(yīng)性[1－2]。

局部線性嵌入(Local Linear Embedding，LLE)是流形學(xué)習(xí)的一種，它的基本思想是發(fā)現(xiàn)隱藏在高維數(shù)據(jù)中不能直接觀察的結(jié)構(gòu)信息，獲得一個能夠保持高維數(shù)據(jù)特征的低維嵌入[3－5]。LLE算法只考慮一個全局最優(yōu)解，在權(quán)值優(yōu)化時只需對局部計算，在計算上簡單可行;在求解低維嵌入時把問題轉(zhuǎn)化為求解一個稀疏矩陣的最小特征值問題，使得LLE算法在運算效率上優(yōu)于其他流形學(xué)習(xí)方法[6－8]。

本文采用了“原始信號－構(gòu)造特征矩陣－數(shù)據(jù)降維(特征提取)－模式識別”的故障診斷模式，其中“數(shù)據(jù)降維”采用了局部線性嵌入方法，使用云神經(jīng)網(wǎng)絡(luò)完成模式識別。為了獲得理想的低維嵌入，本文構(gòu)造一個由振動信號組成的矩陣作為LLE算法的輸入矩陣。與相空間的構(gòu)造方法不同，是在原始信號中分段截取等長數(shù)據(jù)段并把它們組合成一個矩陣作為特征矩陣，最后用云神經(jīng)網(wǎng)絡(luò)對LLE算法得到的低維矩陣的分類效果進行測試[9－10]。對正常和故障轉(zhuǎn)子振動信號的分析說明該方法能有效地用于轉(zhuǎn)子系統(tǒng)故障診斷。

1 局部線性嵌入算法

LLE算法是一種非線性降維算法，它的基本思想是保將高維空間數(shù)據(jù)投影到低維空間中而不改變原有流形在局部的相互關(guān)系。LLE算法包括三個步驟:確定每個點樣本點的鄰域，計算重構(gòu)權(quán)值矩陣W，利用矩陣W計算低維嵌入，具體算法如下。

1.1 尋找每個樣本點的K個近鄰點

設(shè)矩陣 X=(x1，x2，…，xN)，xi是 D 維列向量，根據(jù)度量空間距離:

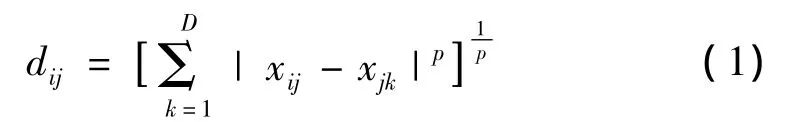
計算任意兩個樣本點之間的歐式距離(p=2)，得出樣本點xi的K個距離中最近的點作為xi的K近鄰。

1.2 計算重構(gòu)權(quán)值矩陣

定義一個誤差函數(shù):

其中:xij(j=1，2，…，K)是 xi的 K 個近鄰點，wij表示 xi和xij之間的權(quán)值，且滿足條件:

將式(3)代入式(2)得:

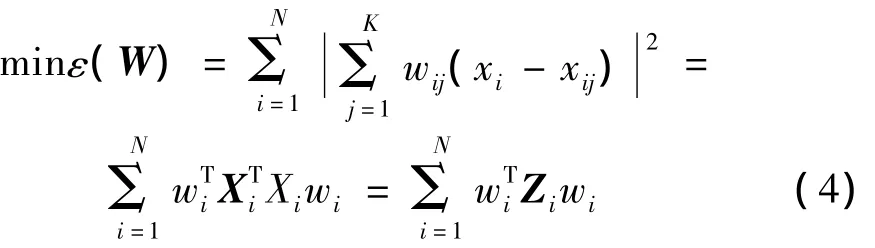
1.3 將所有樣本點映射嵌入到低維空間

映射滿足條件:

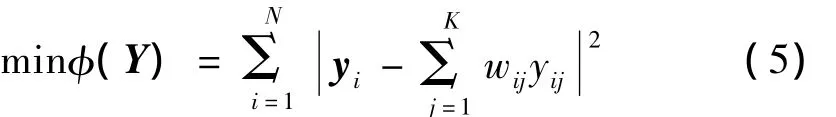
其中:φ(Y)是輸出函數(shù)，yi是 xi的輸出向量，yij(j=1，2，…，k)是yi的k個近鄰點，且滿足兩個條件:和可以存儲在N×N的稀疏矩陣 W 中。當(dāng) xj是 xi的近鄰點時，Wi，j=wij，否則，Wi，j=0。用Wi表示W(wǎng) 矩陣的第i列，Ii表示N ×N 單位矩陣的第 i列，Y 表示輸出向量，即 Y=(y1，y2，…，yN)，則式(5)可寫為:

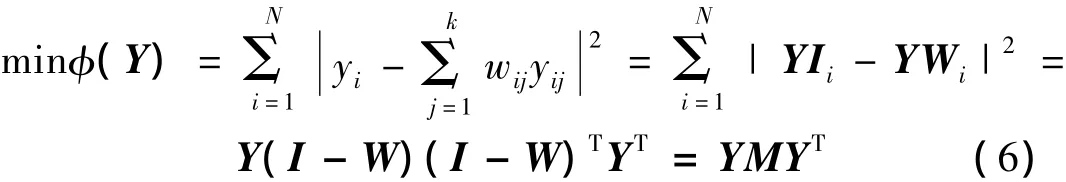
要使損失函數(shù)值最小，則Y取M的d個最小非零特征值所對應(yīng)的特征向量，將M的特征值按從小到大排列，一般地，第一個特征值幾乎等于零，因此取從2～d+1共d個特征值所對應(yīng)的特征向量作為輸出結(jié)果Y。

2 云神經(jīng)網(wǎng)絡(luò)

2.1 云的基本概念

設(shè)U是一個用精確語言描述的定量論域U={x}，T是與U相聯(lián)系的語言值。U中的元素x對于T所表示的定性概念的隸屬度Cr(x)是一個具有穩(wěn)定傾向的隨機數(shù)，Cr(x)∶U→[0，1]，?x∈U，x→Cr(x)。隸屬度在論域上的分布稱為隸屬云，簡稱云。云用期望值Ex、熵En、超熵He三個數(shù)值來表征。

2.2 云發(fā)生器及其改進

給定云的3個數(shù)字特征(Ex，En，He)，產(chǎn)生正態(tài)云模型的若干云滴 drop(xi，μi)(i=1，2，…，n)，稱為正向云發(fā)生器。其中:xi為定性概念的具體量化值;μi為xi屬于定性概念的隸屬度。

已知云模型(Ex，En，He)，有條件x=x0的云發(fā)生器稱為X條件云發(fā)生器，有條件μ=CT(x)=CT(x0)的云發(fā)生器稱為Y條件云發(fā)生器，如圖1所示。相應(yīng)的算法如下[11]:

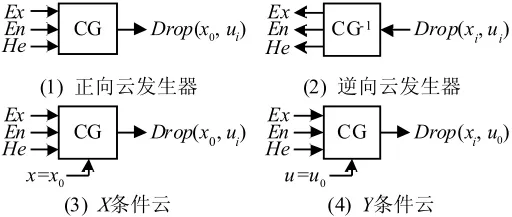
圖1 云發(fā)生器Fig.1 Cloud generator

2.3 云神經(jīng)網(wǎng)絡(luò)

云模型廣泛應(yīng)用于數(shù)據(jù)挖掘等領(lǐng)域[12]，但結(jié)合神經(jīng)網(wǎng)絡(luò)的云理論在工程實踐中還應(yīng)用非常少。其中田永青[13]在簡化的T－S云模型控制器基礎(chǔ)上提出了一種云神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，并應(yīng)用于某地稅收預(yù)測。該網(wǎng)絡(luò)是根據(jù)簡化云模型推導(dǎo)出的多輸入單輸出模型，工程應(yīng)用不便。為此，本文采用文獻(xiàn)[14]提出的云神經(jīng)網(wǎng)絡(luò)模型，結(jié)構(gòu)如圖2所示。該網(wǎng)絡(luò)中，有m個輸入，n個輸出，5層分別是輸入層、云化層、隱含層、逆云化層和輸出層。在云化層使用X正態(tài)云發(fā)生器，在逆云化層使用Y正態(tài)云發(fā)生器，在隱含層使用連續(xù)可導(dǎo)的傳遞函數(shù)。

在學(xué)習(xí)過程中，使用誤差反向傳播算法。設(shè)云神經(jīng)網(wǎng)絡(luò)的輸入為X，輸出為Y，仿真輸出為Ys，隱含層節(jié)點為k個，隱含層傳遞函數(shù)為f。

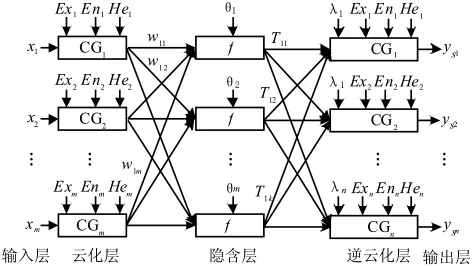
圖2 云神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)Fig.2 Structure of the cloud neural network

當(dāng)輸入為xi(i=1，2，…，m)，則云化層輸出為:

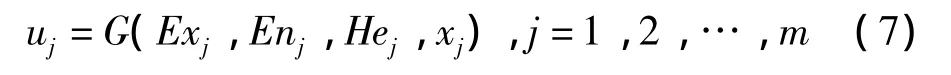
隱含層輸出為:

“不用慌，他懷疑你謀殺是沒有根據(jù)的，有動機，但沒有證據(jù)，你怕什么？再說現(xiàn)在受益人不是咱們，很難說他更懷疑誰，他只是在試探你們，別理他。”

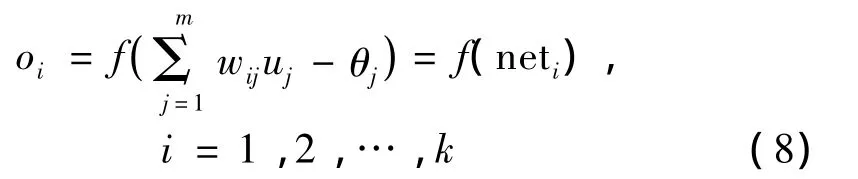
逆云化層輸出為:

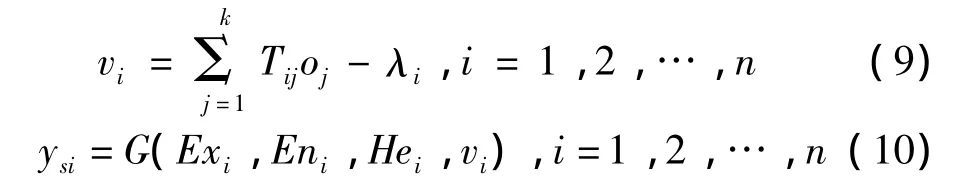
云神經(jīng)網(wǎng)路的性能函數(shù)為:

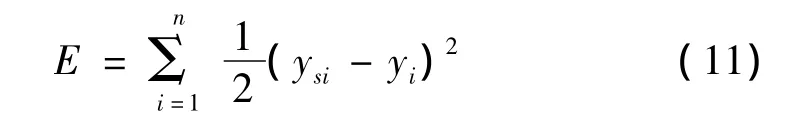
3 故障診斷實驗

3.1 實驗數(shù)據(jù)采集

轉(zhuǎn)子振動實驗臺(如圖3)模擬振動信號，人為制造一些故障來模擬汽輪機轉(zhuǎn)子的振動。實驗裝置包括:轉(zhuǎn)子振動實驗臺、ZXP－4A型數(shù)字測振儀主機、電渦流傳感器、DASP信號采集器以及計算機等。模擬的故障分為3類，包括:轉(zhuǎn)子質(zhì)量不平衡、不對中以及松動和不對中耦合。各種故障模擬的方法為:不平衡故障通過在臨近電渦流傳感器的轉(zhuǎn)子轉(zhuǎn)盤上旋入3～5個螺釘，螺釘要集中以使轉(zhuǎn)子發(fā)生不平衡故障;不對中故障是將聯(lián)軸器換成硬質(zhì)橡膠管，并在軸末端的軸承座底墊上1～2個墊片，人為將軸承座扭轉(zhuǎn)一定角度實現(xiàn);松動和不對中故障耦合則是在一次實驗中加入軸承座松動和轉(zhuǎn)子不對中兩種故障實現(xiàn)。

圖3 轉(zhuǎn)子振動實驗臺Fig.3 Experiment of rotor vibration

故障信號的原始采樣頻率為1 000 Hz，采樣點數(shù)為8 000點，實驗中，轉(zhuǎn)子轉(zhuǎn)速分為1 000 r/min，1 150 r/min和1 200 r/min三種。每個轉(zhuǎn)速下一種故障采樣10組數(shù)據(jù)。

3.2 特征矩陣構(gòu)造

在使用LLE算法之前需要構(gòu)造一個能夠代表振動信號的矩陣。在時間序列分析中，相空間重構(gòu)的理論能夠利用時間序列的特性構(gòu)造一個由時間序列組成的矩陣，但是用相空間重構(gòu)方法構(gòu)造的矩陣作為樣本輸入LLE算法進行測試的結(jié)果表明，分類效果不明顯。本文在相空間重構(gòu)理念的基礎(chǔ)上提出一個新的特征矩陣構(gòu)造方法。

本文所用信號由不平衡、不對中以及不對中加松動三類故障信號組成，分析頻率為1 000 Hz。

如圖4所示，分別截取了三類故障信號的100個點畫出一個原始信號波形示意圖。觀察波形圖可知，不對中信號相對于其他兩種信號比較平滑，出現(xiàn)的局部峰值點比較少;不平衡信號振動比較強烈，局部峰值點比較多。從整體來上，三類信號都表現(xiàn)出了一定的周期性特征，在長度為100個采樣點的范圍內(nèi)每個信號大約有3.5個近似周期;觀察振動信號的局部波形特征，發(fā)現(xiàn)有一些特有的波形會重復(fù)出現(xiàn)，而且各類振動信號的局部特有波形不同。如果能將局部波形差異放大，即可獲得該信號區(qū)別于其他信號的特征矩陣。

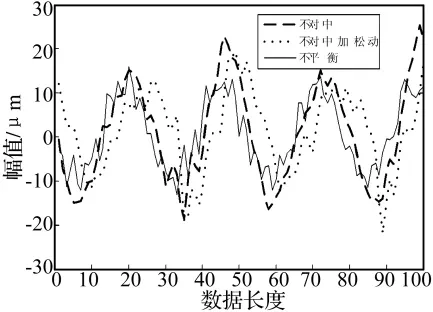
圖4 原始振動信號Fig.4 Original vibration signals

考慮到LLE算法的第一步是求出高維數(shù)據(jù)的K個近鄰點，也就是說在構(gòu)造的特征矩陣的各個樣本點之間搜索距離最近的點，為了體現(xiàn)出某一類信號的特征必須保證計算出的近鄰點之間距離在某一個特定的范圍內(nèi)，那么每一個樣本點信號都能夠用同一類的信號表示。設(shè)時間序列為S(s1，s2，…，sn)，算法步驟如下:

(1)求出S中所有極值點。如果si的模大于si－1，si－2并且大于 si+1，si+2，那么 si就是所要找的極值點。

(2)確定基點。對所有的極值取絕對值，然后求出其算術(shù)平均值，如果極值si大于平均值，那么si就是所要找的基點。

(3)獲得樣本點。以基點為起始點截取一定長度的數(shù)據(jù)作為一個樣本點。取值長度的大小會影響LLE算法近鄰點的選取，本文選取長度為3～4個近似周期的數(shù)據(jù)。

(4)將所有的樣本點逐列排列組成一個矩陣，即所要的特征矩陣。

3.3 故障診斷流程

基于局部線性嵌入和云神經(jīng)網(wǎng)絡(luò)的故障流程如圖5所示。

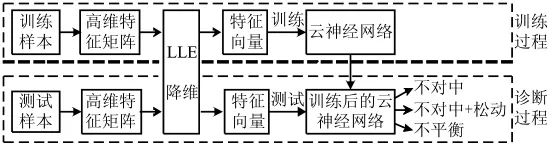
圖5 故障診斷流程圖Fig.5 Process of fault diagnosis

具體診斷步驟如下:

(1)采集轉(zhuǎn)子的故障信號，并分為訓(xùn)練樣本和測試樣本兩部分。

(2)按照3.2中的方法構(gòu)造高維特征矩陣，并運用LLE算法進行降維，降維后的低維特征向量作為云神經(jīng)網(wǎng)絡(luò)的輸入。

(3)以不對中、不對中加松動、不平衡3種模式作為網(wǎng)絡(luò)的輸出，確定網(wǎng)絡(luò)結(jié)構(gòu)，對網(wǎng)絡(luò)進行訓(xùn)練。

(4)用訓(xùn)練后的云神經(jīng)網(wǎng)絡(luò)對測試樣本進行測試。

4 結(jié)果與分析

利用上述方法構(gòu)造一個特征矩陣X，用LLE算法對矩陣X降維后得到了一個低維的矩陣Y，當(dāng)輸出矩陣Y的維數(shù)是2或3的時候，可以用圖形顯示分類效果。當(dāng)維數(shù)高于3維時需要利用分類器來識別，本文采用云神經(jīng)網(wǎng)絡(luò)。

4.1 低維流形

如圖6所示，按照數(shù)據(jù)長度為80個點，分別在轉(zhuǎn)子不對中、不對中加松動和不平衡三種故障信號隨機抽取44個樣本點構(gòu)造了一個132×80的特征矩陣;當(dāng)K=5，d=3時用LLE算法對該特征矩陣降維得到了低維空間表示。從三維圖可以看出每一類數(shù)據(jù)都能比較集中的分布一個特定區(qū)域，3類數(shù)據(jù)在空間分布上有明顯的區(qū)別;二維圖比較清晰地反映了三類數(shù)據(jù)在空間上的區(qū)分程度，不對中信號在V2方向上對應(yīng)于－1，在V1方向上沿著一條直線較為集中分布在－1、－0.5和1三個點的附近;不對中加松動信號沿斜線方向分布在0和－1兩個點的附近分布比較集中，不平衡信號在V1方向分布在1的附近，在V2方向上均勻分布。

4.2 云神經(jīng)網(wǎng)絡(luò)診斷結(jié)果分析

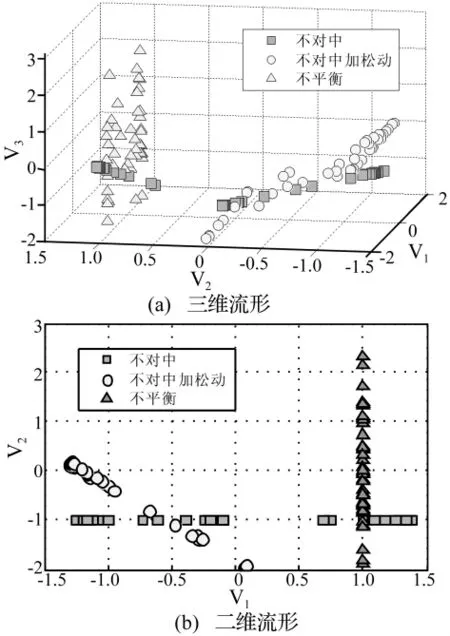
圖6 低維流形圖Fig.6 Lower manifold figure

上述N，m，K，d四個參數(shù)對低維流形都有較大的影響，因此需要進行多次試驗驗證該方法的可行性，并選取一組比較合適的參數(shù)以獲得更好的診斷效果。從三維流形和二維流形圖可以看出，3類數(shù)據(jù)并沒有完全分離，而是在某一個區(qū)域內(nèi)分布比較集中，各類數(shù)據(jù)在空間分布上有明顯的差異。實際上各類數(shù)據(jù)在低維流形上存在一定的交叉區(qū)域，試驗表明LLE算法的參數(shù)K取值過大時，各類數(shù)據(jù)在低維流形上的投影趨于一個區(qū)域，分類效果不明顯;當(dāng)K取值過小時受到LLE算法本身的局限性所得結(jié)果不夠精確，因此需要通過實驗選擇一個最優(yōu)值。其中N和m取值與矩陣構(gòu)造有關(guān)，對低維流形有一定的影響。

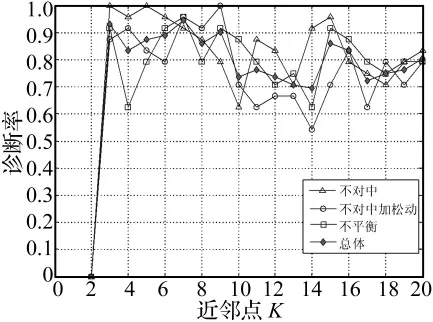
圖7 故障診斷率與近鄰點數(shù)K的關(guān)系Fig.7 The relationship between fault diagnosis rate and nearest neighborhood K

圖7 為當(dāng) N=60，m=44，d=3，云神經(jīng)網(wǎng)絡(luò)(隱層節(jié)點數(shù)為15)的診斷率隨近鄰點數(shù)K變化的曲線，每類故障的診斷率都是經(jīng)過5次實驗取平均值得到的統(tǒng)計結(jié)果。從圖中可以看出，在近鄰點為3－9的范圍內(nèi)時診斷率較高，平均在83.3%以上，在K=7時總體診斷率達(dá)到最大值。隨著近鄰點數(shù)的取值增大，診斷率呈現(xiàn)波動整體診斷率下降，當(dāng)K＞10時，不對中加松動故障的診斷率明顯的下降，而其他兩種類型的故障診斷率基本上在70%以上，分析其可能原因有:

(1)不對中與不對中加松動兩種故障的振動信號都有不對中的故障成分，增加了兩種故障的區(qū)分難度;

(2)近鄰點K取值過大導(dǎo)致診斷率下降，因為LLE算法要求找出一個樣本點的K個最近鄰樣本點并用這些樣本線性表示，K值過大使得線性表示出現(xiàn)誤差。

圖8為當(dāng) N=60，m=44，K=9，云神經(jīng)網(wǎng)絡(luò)(隱層節(jié)點數(shù)為15)的診斷率隨LLE算法嵌入維數(shù)d的變化關(guān)系曲線，可以看出當(dāng)d取3、4時診斷率較高，隨著d的增大診斷率呈下降趨勢。不對中與不對中加松動兩種故障的診斷率隨d的變化趨勢一致，3種故障的診斷率下降是由于輸出在低維空間投影很接近而導(dǎo)致的。實驗發(fā)現(xiàn)，構(gòu)造特征矩陣的數(shù)據(jù)段長度N和個數(shù)m對診斷率也有一定的影響，但影響程度較小。

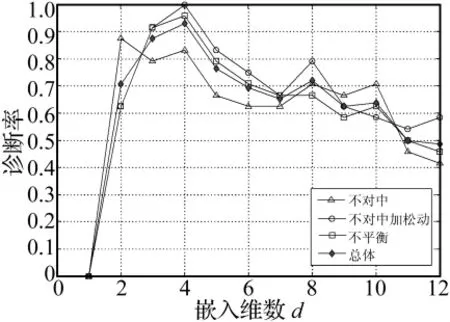
圖8 故障診斷率與嵌入維數(shù)d的關(guān)系Fig.8 The relationship between fault diagnosis rate and embedding dimensionality d

當(dāng)近鄰點數(shù)K=9，嵌入維數(shù)d=4時，3類故障各取13個樣本測試得到的診斷結(jié)果見表1。此外，為了驗證云神經(jīng)網(wǎng)絡(luò)的分類效果，本文還設(shè)計了一個三層BP神經(jīng)網(wǎng)絡(luò)和一個RBF神經(jīng)網(wǎng)絡(luò)，神經(jīng)網(wǎng)絡(luò)的訓(xùn)練樣本和測試樣本均與云神經(jīng)網(wǎng)絡(luò)相同。BP網(wǎng)絡(luò)的隱層節(jié)點數(shù)為12，訓(xùn)練最大步數(shù)選擇為2 000，誤差指標(biāo)為0.001，診斷率見表1。從表中可以看出，每種故障的13個測試樣本中，云神經(jīng)網(wǎng)絡(luò)的錯分樣本數(shù)分別為2個、1個和1個，總體診斷率達(dá)到了89.74%，而BP網(wǎng)絡(luò)的錯分樣本數(shù)分別為3個、2個和2個，總體診斷率為79.49，RBF網(wǎng)絡(luò)的總體診斷率為87.18%，可以看出在訓(xùn)練樣本相同的情況下，云神經(jīng)網(wǎng)絡(luò)的診斷率高于BP網(wǎng)絡(luò)和RBF網(wǎng)絡(luò)，表現(xiàn)出更好的分類性能，從而驗證了本文提出的特征提取方法及診斷方法的可行性。

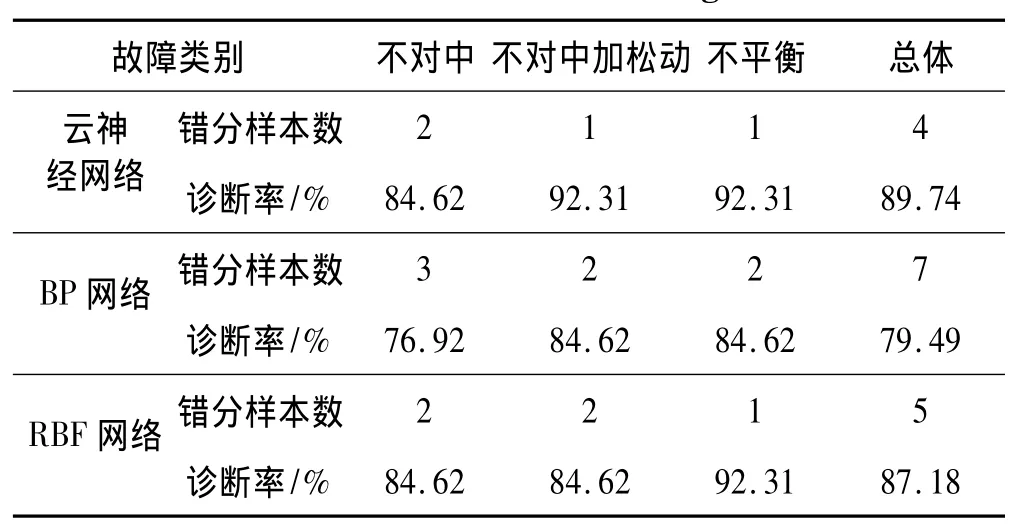
表1 故障診斷結(jié)果Tab.1 The results of fault diagnosis

5 結(jié)論

本文研究了流形學(xué)習(xí)方法在轉(zhuǎn)子故障診斷中的應(yīng)用，并提出了一種利用局部線性嵌入(LLE)算法和云神經(jīng)網(wǎng)絡(luò)的轉(zhuǎn)子故障診斷方法。LLE算法需構(gòu)造一個高維特征矩陣，本文提出了基于峰值對齊的構(gòu)造方法。實驗驗證了該方法構(gòu)造的矩陣可將時間序列的處理與流形學(xué)習(xí)聯(lián)系在一起，能準(zhǔn)確診斷轉(zhuǎn)子的振動故障。同時分析了算法中幾個參數(shù)對診斷結(jié)果的影響，發(fā)現(xiàn)近鄰點數(shù)K和嵌入維數(shù)d對診斷結(jié)果影響較大。與BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)相比，云神經(jīng)網(wǎng)絡(luò)具有更高的診斷率。

致謝:本文受到了東北電力大學(xué)研究生創(chuàng)新基金(2010)資助。特此感謝。

[1]于德介，陳淼峰，程軍圣，等.基于EMD的奇異值熵在轉(zhuǎn)子系統(tǒng)故障診斷中的應(yīng)用[J].振動與沖擊，2006，25(2):24－26.

[2]彭文季，羅興锜.基于小波包分析和支持向量機的水電機組振動故障診斷研究[J].中國電機工程學(xué)報，2006，26(24):164－168.

[3]Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290(5500):2323－2326.

[4]Tenenbaum J B，Silvavd，Langford J C.A global geometric framework fornonlineardimensionality reduction[J].Science，2000，290(5500):2319 －2323.

[5]徐 輝.基于流形學(xué)習(xí)的特征提取[D].西安:西安電子科技大學(xué)，2010.

[6]Ridder D de，Duin R P W.Locally linear embedding for classification[R].Delft，Netherlands:Pattern Recognition Group，Dept of Image Science ＆ Technology，Delft University of Technology，2002.

[7]李偉生，張 勤.基于局部線性嵌入和Haar小波的人臉識別方法[J].計算機工程與應(yīng)用，2011，47(4):181 －187.

[8]馬 瑞，王家廞，宋亦旭.基于局部線性嵌入(LLE)非線性降維的多流形學(xué)習(xí)[J].清華大學(xué)學(xué)報(自然科學(xué)版)，2008，48(4):583 －586.

[9]Samuel K，Martin D L.Face detection in gray scale images using locally embeddings[J].Computer Vision and Image Understanding，2007，105(1):1 －20.

[10]Cox T F，Cox M A A.Multidimensional scaling(2nded.)[M].Chapman and Hall，2001.

[11]劉常昱，馮 芒，戴曉軍，等.基于云X信息的逆向云新算法[J].系統(tǒng)仿真學(xué)報，2004，16(11):2417－2420.

[12]楊薛明，苑津莎，王劍鋒，等.基于云理論的配電網(wǎng)空間負(fù)荷預(yù)測方法研究[J].中國電機工程學(xué)報，2006，26(6):30－36.

[13]田永青.基于云模型的數(shù)據(jù)挖掘算法的研究與應(yīng)用[D].上海:上海交通大學(xué)，2003.

[14]徐宗本，樊忠澤.基于云神經(jīng)網(wǎng)絡(luò)的空間推進系統(tǒng)故障檢測與診斷[J].兵工學(xué)報，2009，30(6):727 －732.