柔性基礎(chǔ)主動(dòng)隔振系統(tǒng)的縮聚建模和時(shí)滯問(wèn)題研究

宋 攀，董興建，孟 光

(上海交通大學(xué) 機(jī)械系統(tǒng)與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室，上海 200240)

浮筏裝置是一個(gè)集多種動(dòng)力學(xué)元件為一體的混合動(dòng)力學(xué)系統(tǒng)，其結(jié)構(gòu)緊湊，附加質(zhì)量少，隔振效果好，且具有良好的抗沖性能。隨著現(xiàn)代浮筏裝置向大型化和輕型化方向的發(fā)展，浮筏結(jié)構(gòu)設(shè)計(jì)有以下不足之處，首先在現(xiàn)有的分析設(shè)計(jì)過(guò)程中假定筏架和基礎(chǔ)是剛性的，忽略了振動(dòng)過(guò)程中產(chǎn)生的彈性變形;其次，上述浮筏隔振裝置的實(shí)質(zhì)是一種振動(dòng)被動(dòng)控制技術(shù)，對(duì)超低頻振動(dòng)和寬帶隨機(jī)振動(dòng)的隔振效果并不理想。為了進(jìn)一步提高艦艇的聲隱身性能，有必要在浮筏隔振裝置中引入作動(dòng)器，然而傳感器信號(hào)的采集、傳輸和作動(dòng)器的作動(dòng)過(guò)程等都不可避免的存在時(shí)滯現(xiàn)象。力學(xué)工作者在主動(dòng)隔振研究中采用了很多控制理論中的成熟方法[1－2]，如特征結(jié)構(gòu)配置方法，自適應(yīng)控制，H∞控制[3－4]。在建立了反映系統(tǒng)力學(xué)本質(zhì)的數(shù)學(xué)模型之后，對(duì)其實(shí)施振動(dòng)主動(dòng)控制就不存在理論上的特殊性。但是對(duì)于主動(dòng)隔振系統(tǒng)中的時(shí)滯現(xiàn)象以及時(shí)滯對(duì)控制效果的影響，目前尚沒(méi)有文獻(xiàn)報(bào)導(dǎo)。以往人們?yōu)榱死碚摲治龊涂刂破髟O(shè)計(jì)的方便，總是忽略時(shí)滯，但即使是小時(shí)滯量也可能會(huì)導(dǎo)致在系統(tǒng)不需要能量時(shí)向其輸入能量，進(jìn)而引起控制效率的下降，甚至控制系統(tǒng)失穩(wěn)。另外，我們發(fā)現(xiàn)，全模型最優(yōu)控制需要測(cè)出受控對(duì)象的所有狀態(tài)參數(shù)，而對(duì)于大型浮筏這樣的復(fù)雜結(jié)構(gòu)，其狀態(tài)參數(shù)通常很多，這必然導(dǎo)致測(cè)試和在線數(shù)據(jù)處理的工作量很大，使得時(shí)滯效應(yīng)變得非常明顯，嚴(yán)重影響控制效果。而現(xiàn)有的浮筏隔振裝置的建模方法，即多剛體法、波分析法[5]，又往往只考慮結(jié)構(gòu)的剛性而忽略彈性。有限元法雖然理論上可適用于任意復(fù)雜的結(jié)構(gòu)，然而，為了保證計(jì)算精度，有限元模型必然會(huì)很大，給進(jìn)一步的動(dòng)力分析帶來(lái)很大不便。

為了解決以上技術(shù)難題，本文以浮筏裝置為研究對(duì)象，針對(duì)其建模問(wèn)題和時(shí)滯主動(dòng)控制問(wèn)題進(jìn)行研究。考慮中間質(zhì)量的柔性和基礎(chǔ)的彈性，建立復(fù)雜柔性主動(dòng)隔振系統(tǒng)模型，并通過(guò)把裝置中彈性體的有限元模型在物理空間中進(jìn)行減縮，建立各自的超單元，然后在把這些超單元與裝置中的其它結(jié)構(gòu)一起建立總體模型;將主動(dòng)隔振的思想引入浮筏隔振系統(tǒng)，并率先在主動(dòng)隔振系統(tǒng)中考慮作動(dòng)器的時(shí)滯效應(yīng)，將時(shí)滯連續(xù)控制系統(tǒng)離散為形式上不包含有時(shí)滯的標(biāo)準(zhǔn)離散形式，然后按照離散最優(yōu)控制方法進(jìn)行控制設(shè)計(jì)。因最優(yōu)離散控制律直接從時(shí)滯微分方程中得出，且推導(dǎo)中無(wú)近似處理和估計(jì)，因此該方法易于保證控制系統(tǒng)的性能和穩(wěn)定性。

1 基本理論

1.1 柔性耦合系統(tǒng)超單元縮聚[6]

假設(shè)任意結(jié)構(gòu)的無(wú)阻尼動(dòng)力學(xué)方程為:

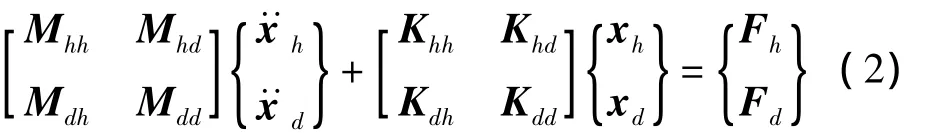
通常來(lái)說(shuō)，保留自由度應(yīng)包括有外載荷作用的自由度、給定位移的自由度、與其它單元連接的節(jié)點(diǎn)自由度和要考察的自由度等，因此式(2)中的Fd應(yīng)為零向量。把式(2)中的第二式展開(kāi)，有:

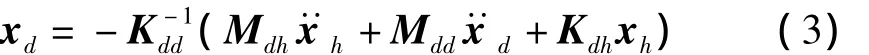
在式(3)中，由于括號(hào)中的第一和第二項(xiàng)均不與xh成線性關(guān)系，因此很難直接從該式中求得xd與xh的關(guān)系矩陣。為此假定:

則有:

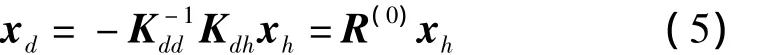
顯然，Xd和Xh之間的關(guān)系矩陣R(0)忽略了式(3)中慣性力的影響，故該矩陣只有在靜態(tài)時(shí)才是精確的，而對(duì)于動(dòng)力學(xué)問(wèn)題必然存在誤差。構(gòu)造n×k階坐標(biāo)轉(zhuǎn)換矩陣P(0)為:

其中:I為k×k階單位矩陣。假定與此結(jié)構(gòu)對(duì)應(yīng)的超單元的剛度矩陣和質(zhì)量矩陣分別為和則有:

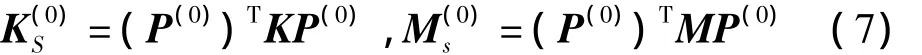
相應(yīng)地該超單元的自由振動(dòng)方程為:

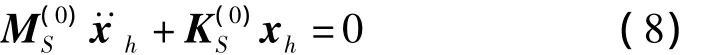
式(8)即為經(jīng)典超單元法，此處的保留自由度即超單元的自由度是事先給定的，不能進(jìn)行優(yōu)化，這必然使得關(guān)系矩陣R(0)的精度很低。相應(yīng)地，建立在該基礎(chǔ)上的超單元的剛度矩陣和質(zhì)量矩陣也存在很大的誤差，且隨著振動(dòng)頻率的增加，該誤差越來(lái)越大。為了解決該問(wèn)題，對(duì)前面給出的關(guān)系矩陣零階近似R(0)進(jìn)行修正。從式(8)可得:

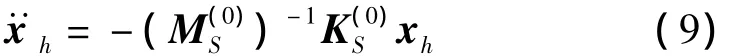
考慮到式(5)、式(9)和式(3)，并整理可得:

從式(10)可得關(guān)系矩陣的第一次近似值:

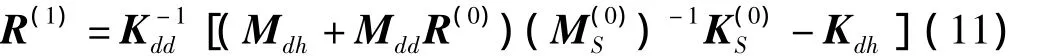
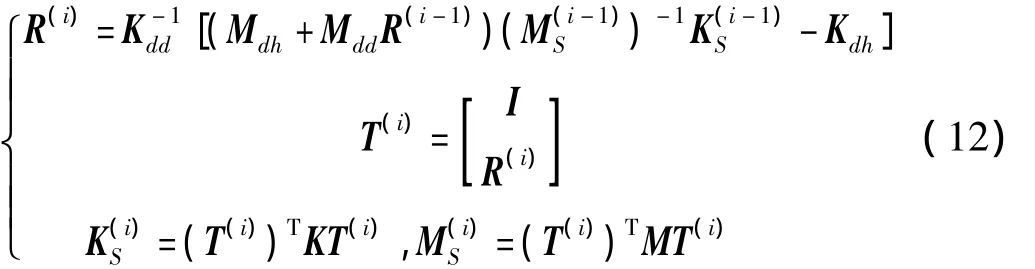
1.2 線性時(shí)滯系統(tǒng)的標(biāo)準(zhǔn)離散狀態(tài)方程

考慮如下n自由度的結(jié)構(gòu)模型:

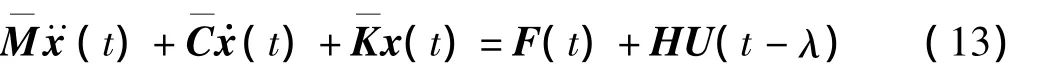
其中:x(t)∈Rn是基礎(chǔ)、筏架和質(zhì)量塊的絕對(duì)位移;M分別是系統(tǒng)經(jīng)超單元縮聚后的質(zhì)量，阻尼和剛度矩陣;U(t－λ)∈Rr為控制力向量;λ為時(shí)滯量為控制力位置矩陣;F(t)為外激勵(lì)載荷。假定時(shí)滯量λ可描述為如下形式:

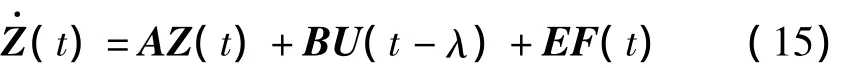
其中:

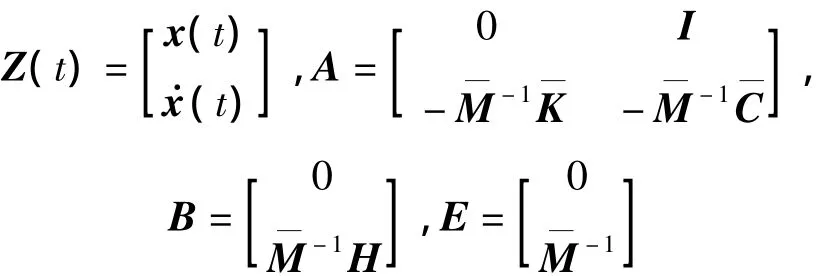
設(shè)在連接的控制對(duì)象和控制器間有一零階保持器連接，即:

式(16)表明，作動(dòng)器在相鄰兩個(gè)采樣點(diǎn)間按常值對(duì)系統(tǒng)施加控制力。U(k)實(shí)際上代表第k步控制U(kT)，為表達(dá)方便文中其他變量表達(dá)同此。

考慮到時(shí)滯量不一定為采樣周期的整數(shù)倍，將狀態(tài)空間變?yōu)殡x散形式:

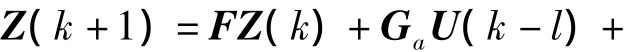
1.3 控制律的設(shè)計(jì)

按照最優(yōu)控制設(shè)計(jì)方法，當(dāng)進(jìn)行最優(yōu)控制設(shè)計(jì)時(shí)，可不考慮外部激勵(lì)項(xiàng)。對(duì)于如下線性離散定常系統(tǒng)

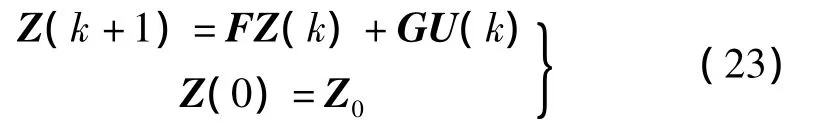
給定二次型性能指標(biāo)函數(shù)為:

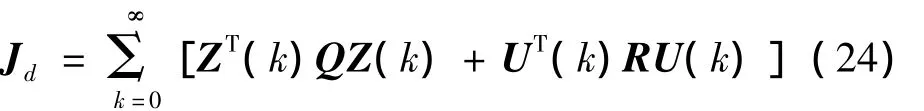
其中:Q是非負(fù)定對(duì)稱陣，R是正定對(duì)稱陣。設(shè)S(k)是如下離散Riccatik)差分方程的解:

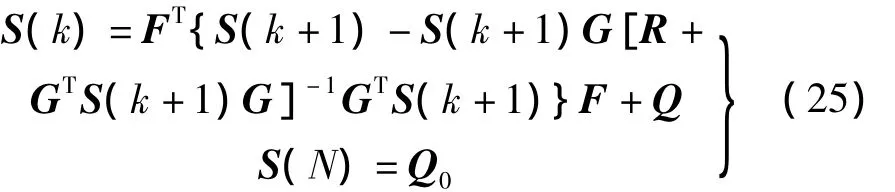
對(duì)于任何非負(fù)定對(duì)稱陣Q0有:

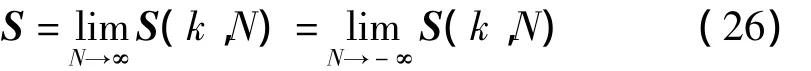
存在，且S是與Q0無(wú)關(guān)的常數(shù)陣。而且，S是如下離散Riccati代數(shù)方程:

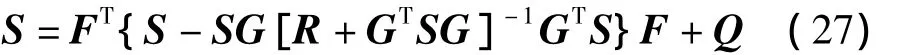
的唯一正定對(duì)稱陣。則穩(wěn)態(tài)控制律可表達(dá)如下:

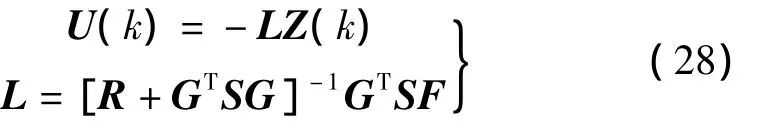
此控制律可使式(24)所示的性能指標(biāo)函數(shù)Jd極小。

因?yàn)槭?24)所示的性能指標(biāo)函數(shù)只能夠保證系統(tǒng)采樣點(diǎn)上具有好的響應(yīng)性能，不能保證系統(tǒng)在采樣點(diǎn)也具有良好的響應(yīng)性能，甚至可能在采樣點(diǎn)間隱藏著振蕩現(xiàn)象。為使系統(tǒng)具有令人滿意的連續(xù)響應(yīng)性能，目標(biāo)函數(shù)取連續(xù)的二次型函數(shù)將能反應(yīng)實(shí)際系統(tǒng)的性能要求。因此，考慮如下連續(xù)二次型目標(biāo)函數(shù):

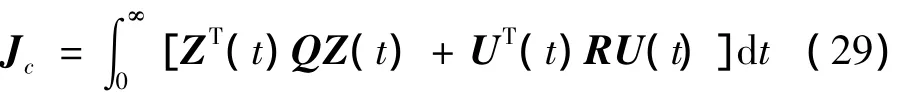
式(29)可進(jìn)一步表示為:

其中:

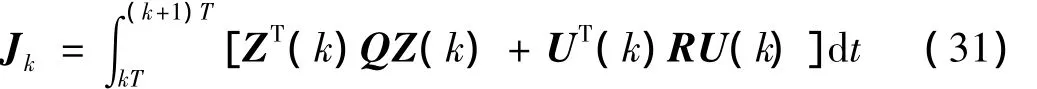
因此，現(xiàn)在問(wèn)題變?yōu)閷?duì)式(19)所示的離散狀態(tài)方程，尋求最優(yōu)控制式所示的性能指標(biāo)Jc極小，從而可以采用式(23)～式(28)所示的方法進(jìn)行求解，最優(yōu)控制可表達(dá)為:

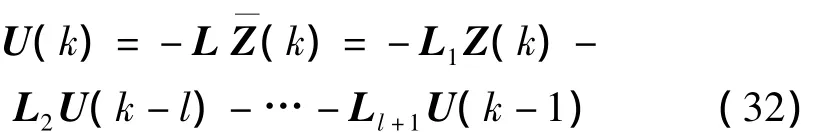
其中:L1～Ll+1分別是L的相應(yīng)維數(shù)的分塊矩陣，由式(32)可見(jiàn)，此時(shí)的最優(yōu)控制除直接的線性反饋外，還包含前l(fā)拍控制量的線性組合。

2 數(shù)值分析

圖1給出了一浮筏裝置的簡(jiǎn)化模型[6]，m1=100 kg和m2=120 kg表示被隔振機(jī)械;筏A架與基礎(chǔ)B的尺寸分別為1.2 m ×0.8 m ×0.02 m 和2.8 m ×0.8 m ×0.04 m，基礎(chǔ)B的兩短邊簡(jiǎn)支、兩長(zhǎng)邊自由;上下兩層彈簧隔振k1=1.0×105N/m，k2=5.0×105N/m，材料的彈性模量 E=2.0 ×1011N/m2，密度為 ρ=7 800 N/m3。

基于浮筏系統(tǒng)為對(duì)象，以降低振源引起自身及彈性基礎(chǔ)振動(dòng)幅值為目標(biāo)，并假定只在如圖1所示位置施加主動(dòng)控制，即在板式筏架上下兩層與被隔振機(jī)械對(duì)位的直線上安裝四個(gè)主動(dòng)隔振器。我們知道，設(shè)備放置在筏架上，浮筏基座又與殼體彈性連接。浮筏裝置一方面可以減小放置在筏架上的機(jī)組擾動(dòng)源自身振動(dòng)，另一方面可是使柴油機(jī)和電機(jī)發(fā)出的機(jī)械噪聲緩沖衰減，不能或較少傳出潛艇外，達(dá)到隱身的作用。為了考察筏架上設(shè)備自身振動(dòng)，以及浮筏與潛艇連接板的隔振效果，并且考慮到浮筏結(jié)構(gòu)的對(duì)稱性，選取如圖1所示的兩個(gè)目標(biāo)點(diǎn)。激勵(lì)力采用0～50 Hz的白噪聲，持續(xù)時(shí)間取為20 s，采樣周期取為T(mén)=0.002 s，性能指標(biāo)式(24)中Q和R依據(jù)經(jīng)驗(yàn)選取;數(shù)值計(jì)算采用四階龍格庫(kù)塔法。

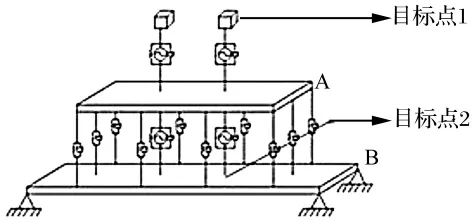
圖1 浮筏模型主動(dòng)控制施加點(diǎn)與目標(biāo)點(diǎn)示意圖Fig.1 The locations of active control and the target points of the floating raft model

2.1 超單元縮聚

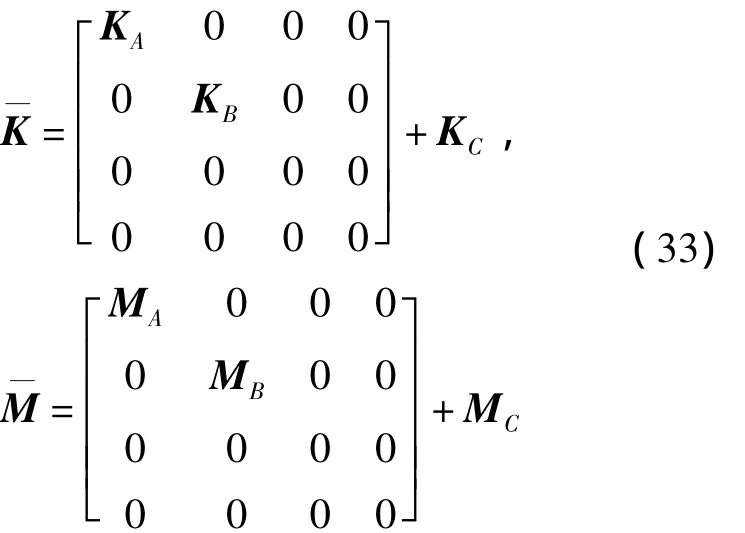
由于筏架和基礎(chǔ)均是彈性的，因此在對(duì)該系統(tǒng)建模之前首先用常規(guī)方法對(duì)筏架和基礎(chǔ)進(jìn)行有限元建模。由于彈簧只有z方向的位移，因此選擇圖1中筏架A上與彈簧阻尼器相連的12個(gè)節(jié)點(diǎn)上z方向的線位移為保留自由度得到筏架超單元?jiǎng)偠染仃嚭唾|(zhì)量矩陣分別為KA和MA。同樣，選擇圖1中基礎(chǔ)B上與彈簧阻尼器相連的12個(gè)節(jié)點(diǎn)上Z方向的線位移為保留自由度得到的基礎(chǔ)模型超單元的剛度矩陣和質(zhì)量矩陣分別為KB和MB。將筏架和基礎(chǔ)的超單元?jiǎng)偠染仃嚭唾|(zhì)量矩陣與浮筏的其它部件組裝成結(jié)構(gòu)的總剛度矩陣和總質(zhì)量矩陣如式(33)，其中，KC和MC分別為由彈簧和機(jī)械在系統(tǒng)總體坐標(biāo)中形成的剛度矩陣和質(zhì)量矩陣。當(dāng)浮筏的總體剛度矩陣和質(zhì)量矩陣建立以后，就可以對(duì)其進(jìn)行動(dòng)態(tài)性能分析。

將完整未縮聚模型在有限元軟件中所求得的系統(tǒng)固有頻率作為精確解。表1是完整模型與降階模型的前二十階固有頻率比較。可以看出，用本文提出的超單元建模方法建立起來(lái)的有限元降階模型共有26個(gè)自由度，顯然它比未降階的模型小得多，而用該降階模型求得的系統(tǒng)前二十階固有頻率與精確解基本吻合。

2.2 最大時(shí)滯量的確定和控制效果比較

當(dāng)控制系統(tǒng)中不存在時(shí)滯，即λ=0時(shí)，式(29)所示的連續(xù)形式性能指標(biāo)所確定的最優(yōu)控制律對(duì)存在時(shí)滯的結(jié)構(gòu)進(jìn)行振動(dòng)控制，結(jié)構(gòu)各節(jié)點(diǎn)的峰值絕對(duì)位移和峰值控制力值隨時(shí)滯量λ的變化曲線由圖2所示。可以看出，結(jié)構(gòu)穩(wěn)定的最大允許時(shí)滯量可近似確定為λ=0.000 4 s。由此可知，控制系統(tǒng)中時(shí)滯問(wèn)題應(yīng)得到人們的足夠重視，否則控制系統(tǒng)有可能發(fā)生不穩(wěn)定現(xiàn)象。

當(dāng)采用的是線性離散定常性能指標(biāo)Jc進(jìn)行控制律設(shè)計(jì)時(shí)。施加主動(dòng)控制前后的系統(tǒng)響應(yīng)對(duì)比，如圖3所示。圖4為結(jié)構(gòu)各個(gè)目標(biāo)點(diǎn)的峰值響應(yīng)和峰值控制力隨時(shí)滯λ的變化曲線，可以看出，本文所提控制方法不但較好的控制結(jié)構(gòu)的峰值響應(yīng)，而且即使控制系統(tǒng)中存在較大的時(shí)滯量，所提控制方法仍能保證控制系統(tǒng)的穩(wěn)定性。同時(shí)，當(dāng)選擇合適的時(shí)滯量時(shí)能夠在較小的控制代價(jià)情況下，達(dá)到更好的控制效果。

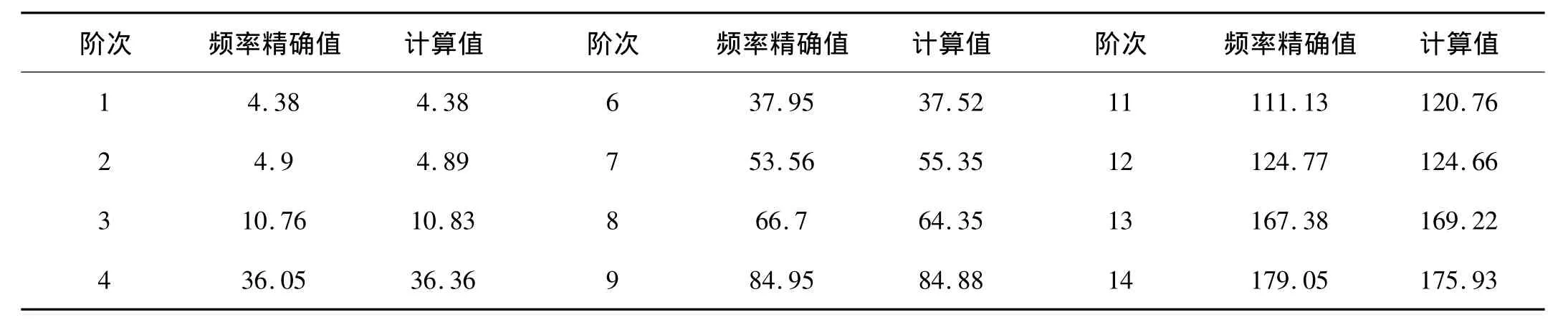
表1 完整模型頻率與降階模型頻率(Hz)Tab.1 The frequency of the complete model and reduced model(Hz)

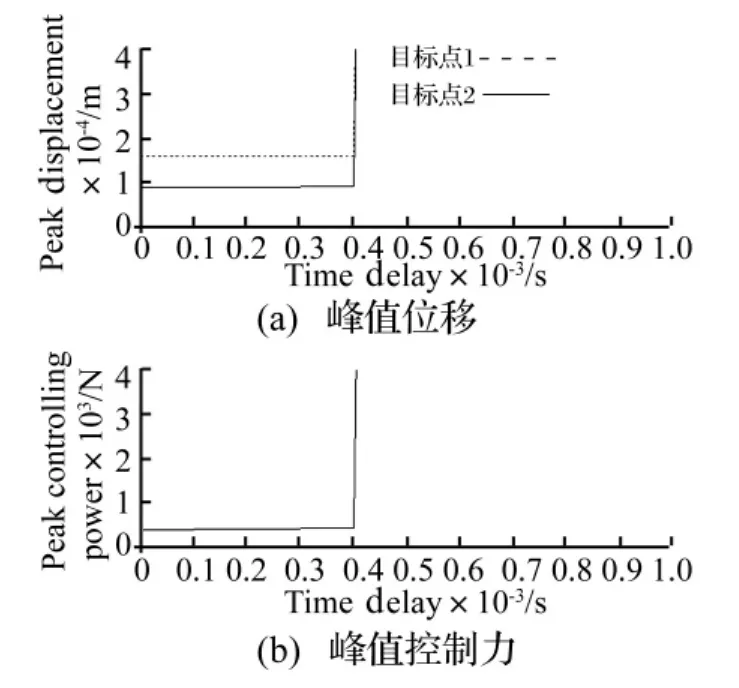
圖2 用無(wú)時(shí)滯時(shí)所設(shè)計(jì)的控制律對(duì)有時(shí)滯時(shí)結(jié)構(gòu)進(jìn)行控制的峰值響應(yīng)Fig.2 The peak response of the control system with delay controled by the control law designed for the system without time delay

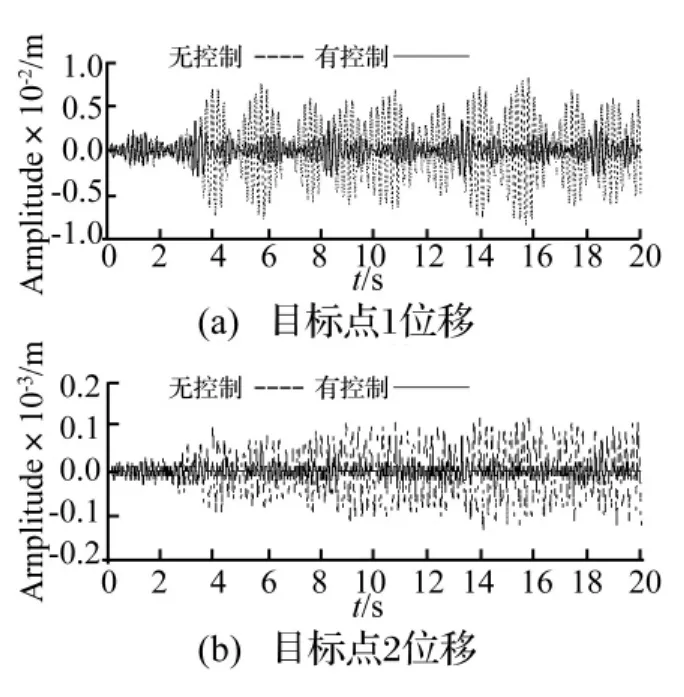
圖3 各目標(biāo)點(diǎn)響應(yīng)對(duì)比(λ =0.2 s，T=0.002 s)Fig.3 Comparison of the response of the target points

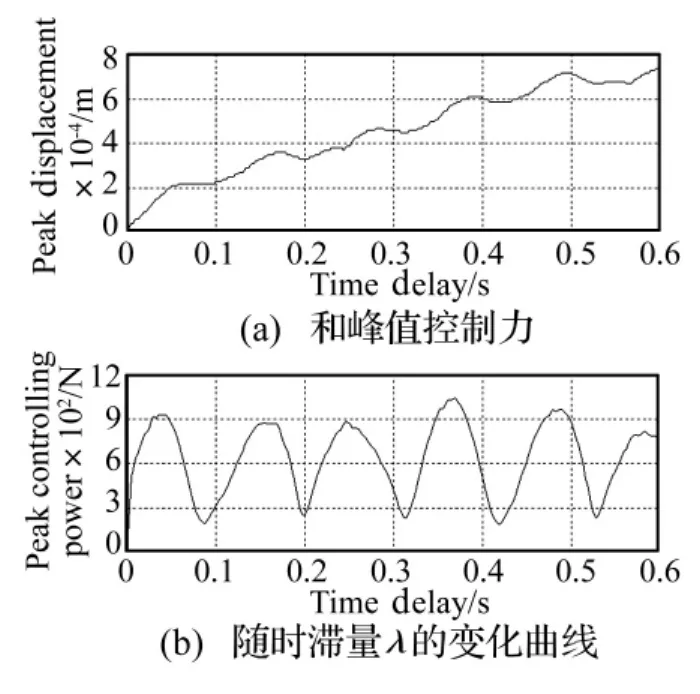
圖4 目標(biāo)點(diǎn)2峰值位移響應(yīng)Fig.4 Curves of the peak displacement response

3 結(jié)論

本文以復(fù)雜柔性耦合主動(dòng)隔振系統(tǒng)為對(duì)象，根據(jù)受控對(duì)象的部分狀態(tài)參數(shù)對(duì)輸出狀態(tài)控制器進(jìn)行設(shè)計(jì)，并考慮到主動(dòng)隔振系統(tǒng)中作動(dòng)器不可避免的時(shí)滯問(wèn)題，通過(guò)分析，結(jié)論如下:

(1)超單元縮聚方法建立起來(lái)的降階模型不僅在規(guī)模上遠(yuǎn)遠(yuǎn)小于未降階的有限元模型，而且能很好地保持原系統(tǒng)的中、低頻動(dòng)態(tài)特性;

(2)通過(guò)將時(shí)滯微分方程離散化，在狀態(tài)變量中增加與時(shí)滯量相關(guān)的前若干步控制項(xiàng)，將時(shí)滯差分方程轉(zhuǎn)換成形式上不包含時(shí)滯項(xiàng)的標(biāo)準(zhǔn)差分方程形式，采用二次型性能指標(biāo)為目標(biāo)函數(shù)設(shè)計(jì)控制律。該控制方法具有良好的控制效果，即使控制系統(tǒng)中存在較大的時(shí)滯量，所提控制方法仍能保證控制系統(tǒng)的穩(wěn)定性。

(3)以主動(dòng)隔振系統(tǒng)的隔振性能為目標(biāo)函數(shù)，將時(shí)滯量作為一個(gè)控制器設(shè)計(jì)參數(shù)，通過(guò)選擇合適的時(shí)滯量可以在控制代價(jià)很小的情況下達(dá)到很好的控制效果。

總之，控制系統(tǒng)中的時(shí)滯存在潛在的利用價(jià)值，在對(duì)時(shí)滯抑制進(jìn)行研究的同時(shí)，還應(yīng)深入研究時(shí)滯的利用問(wèn)題

[1]Chen K T，Chou C H，Chang S H，et al.Intelligent active vibration controlin an isolation platform[J].Applied Acoustics，2008，69(11):1063 －1084.

[2]Fei H Z，Zheng G T，Liu Z G.An investigation into active vibration isolation based on predictive control:Part I:Energy source control[J].Journal of Sound and Vibration，2006，296(1－2):195－208.

[3]Kerber F，Hurlebaus S，Beadle B M，et al.Control concepts for an active vibration isolation system[J].Mechanical Systems and Signal Processing，2007，21(8):3042 －3059.

[4]Hu Y R，Ng A.Active robust vibration control of flexible structures[J]. JournalofSound and Vibration，2005，288(1－2):43－56.

[5]W C J，W R G.Vibrational power transmission in a finite multi-supported beam[J].Journal of Sound and Vibration，1995，181(1):99－114.

[6]瞿祖清.結(jié)構(gòu)動(dòng)力縮聚技術(shù)理論與應(yīng)用[M].上海:上海交通大學(xué)出版社，1998.