強載荷下結構動力響應與損傷的跨尺度分析

湯軼群，李兆霞

(東南大學 土木工程學院工程力學系，南京 210096)

整體結構的失效總是起始于局部的損傷累積，然而局部損傷與整體結構是分別處于局部微、細觀尺度與整體結構尺度這樣兩個不同量級的空間尺度上，所以結構損傷失效過程成為一個跨尺度演化的過程。現行結構分析方法多在單一尺度上進行，在結構整體大尺度上，構件局部損傷及其對結構劣化的影響難以準確模擬;為了關注結構中的易損局部細節，若整體精細模擬，則節點數及單元數會非常龐大，使得模擬無法實現或影響計算效率[1－2]。應用跨尺度分析方法可以很好的解決這一問題，同時分析結構響應及其局部易損部位的損傷演化過程。

對大跨結構的整體或局部不同部位的描述，其適用的理論和尺度范圍取決于描述目的和主要考察對象。從結構全尺度、局部構件尺度和損傷細節尺度三個方面建立多尺度模型時，各個模型尺度所關注的分析對象、適用的理論以及有限元單元特征長度都應有所不同:① 大型工程結構全尺度，其尺度范圍在100～103m，適用結構力學理論，分析結構內力;② 梁、柱、板、殼等構件尺度，其尺度范圍在10－3～100m，適用于材料力學、彈性理論，分析構件名義應力;③ 含缺陷的節點細部構造，其尺度范圍在10－6～10－3m，適用于宏、細觀損傷理論，分析熱點應力、損傷演化[2]。

圖1以局部構件模型為例，給出了典型的跨尺度(局部構件尺度與細觀尺度)有限元模型各組成部分。該等截面梁分別由左邊的精細實體單元模型和右邊的宏觀梁單元模型組成，宏觀梁單元模型在整體結構中屬于無缺陷且始終處于彈性階段的部分，而精細實體單元模型的引入是為了分析結構中的缺陷部位。由于應力集中區域的應力梯度較大以及損傷理論的適用范圍要求，需要把局部缺陷部位的單元網格細化，于是從宏觀的構件尺度到細觀的損傷尺度便需要通過跨尺度界面及過渡區域連接起來。在跨尺度界面上，根據研究對象的需要選取相應的單元連接方法，是多尺度有限元建模中的重點內容。

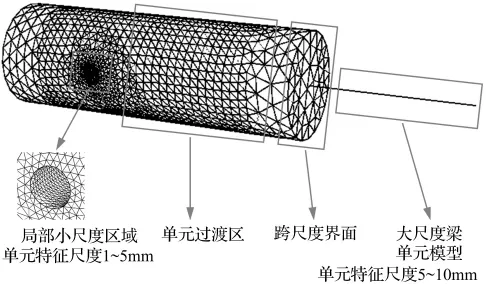
圖1 跨尺度模型的基本組成部分Fig.1 The fundamental component of the trans-scale module

目前在有限元軟件中實現不同單元間的連接主要有下面三種方法:① 直接寫入節點位移約束方程;②建立耦合單元;③ 建立過渡單元[3－14]。這些方法的本質是一樣的，都是為了建立不同類型單元間的節點位移關系。文中以以更加靈活、自由的寫入節點位移約束方程為例，討論兩種基本的建立方法:① 通過滿足兩種不同尺度模型在跨尺度界面上的位移協調建立節點位移約束方程;② 通過滿足兩種不同尺度模型在跨尺度界面上的做功相等建立節點位移約束方程。通過對以上兩種單元連接方法的詳細對比分析，對于更加方便地建立能夠準確反映局部損傷細節的多尺度有限元模型有著十分積極的意義。

配合跨尺度界面上的單元連接方法，本文還在局部小尺度區域引入了塑性損傷耦合的本構模型，真正實現了跨尺度分析。為了驗證本文跨尺度分析方法的正確性，以一鋼桁架結構為例分別建立多尺度有限元模型和單一尺度精細單元模型配合實驗進行驗證，并對兩種模型進行了抗震分析。計算結果表明，運用本文跨尺度分析方法所建立的多尺度有限元模型能夠準確地反映局部節點細節，可以替代單一尺度模型進行強載荷下的結構動力響應與損傷分析，并且能夠大大地提高計算效率。

1 跨尺度界面連接方法

在多尺度有限元模型的跨尺度界面上，可以通過節點位移約束方程把不同類型單元上的節點連接起來[15]，約束方程是一種聯系自由度值的線性方程，其形式如下:

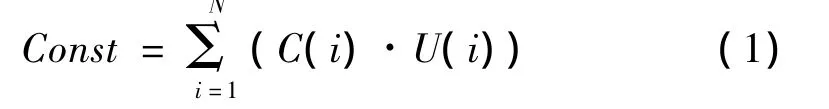
式中:U(i)為節點i的位移自由度項，C(i)為節點i的位移自由度項的系數，N為參與連接的點自由度總數。

1.1 跨尺度界面位移協調方法

如圖2所示，在跨尺度界面上小尺度精細單元模型上的某一節點與大尺度梁單元節點之間的位置關系，并在跨尺度連接界面處建立局部坐標系xyz。不同尺度模型在界面上的自由度按照平截面原則進行傳遞[16－17]。在界面上，以大尺度模型上的節點A為主節點，小尺度模型上的各個節點Bi為從節點，相當于在A點與各個Bi點之間建立一個剛性梁，以保證它們之間的位移協調。針對圖2的三維局部坐標系，假設界面的轉角很小，可以建立節點位移約束方程如下:

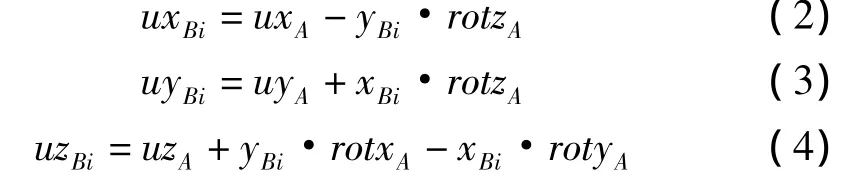
其中:ux，uy，uz分別為 x，y，z方向的位移，rotx，roty，rotz分別為 x，y，z軸的轉角。

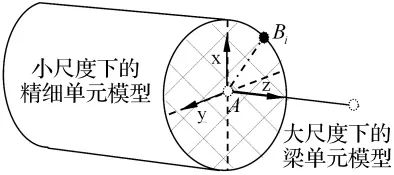
圖2 雙尺度模型在跨尺度界面上節點之間關系示意圖Fig.2 The relationship between nodes on the trans-scale boundary

為保證跨尺度界面上位移的協調性，恰當的提法應該是要求變形后兩種模型在跨尺度界面上各點位移沿垂直于該面方向(即平行于梁單元軸線方向)的分量相同，即兩類單元在跨尺度界面上仍然保持貼合，但不能要求兩種模型在界面上各點位移沿面內方向(即垂直于梁單元軸線方向)的分量相同，因為梁單元忽略了該方向的位移變化。如果要求兩類單元在跨尺度界面內方向上的位移一致，就是強迫小尺度下的精細單元模型在跨尺度界面面內方向的應變為零。這個不恰當的強制條件會使跨尺度界面處的應力分布不同于實際情況，使計算結果失真。因此可以說這是一種剛性的連接方法，該方法要求跨尺度界面要處于線彈性小變形范圍內，且要遠離局部應力集中區域，以保證所關注的局部缺陷部位的計算結果是比較準確的。

1.2 跨尺度界面應力協調方法

為了滿足大尺度下的梁單元與小尺度下的精細單元模型在跨尺度界面處應力的連續性，假設在界面上的做功相等，并按材料力學原理求解界面應力，可推導得到在各種力作用下梁單元與精細單元耦合的多點位移約束方程。其中，小尺度模型在跨尺度界面上的應力分布都是按照材料力學理論在一定假設的基礎上推導得出的，所以整個跨尺度界面也是要偏向于桿件屬性的，必須符合平截面假定，且處于線彈性、小變形范圍內。假如在跨尺度界面上滿足了彈性、小變形的假設，便可以根據疊加原理將跨尺度界面連接分成軸向拉壓、純彎曲、剪切、純扭四種情況，其中純彎曲和剪切情況在跨尺度界面內又可以分為兩個方向，于是便可以得到六個等式。這六個等式分別對應于六種不同的梁單元自由度。等式的具體建立過程如下:

如圖3，在軸向拉伸Fz的作用下，小尺度模型在跨尺度界面上只有z向正應力。所以在界面(z=0)處，可以根據做功相等得到下式:

其中:Fz是梁單元的軸力，w為跨尺度界面上梁單元節點的軸向位移，σz為跨尺度界面上小尺度模型的軸向應力，W是小尺度模型在界面上某點的軸向位移(以坐標為自變量的函數)，A為跨尺度界面上小尺度模型總面積。

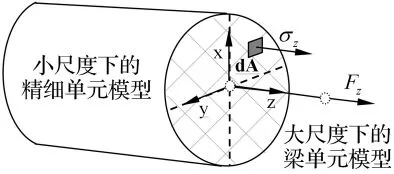
圖3 軸向拉伸作用下雙尺度模型在界面上的應力分布Fig.3 The stress distribution on the trans-scale boundary under the pull load

如果研究對象細長，則跨尺度界面處小尺度模型上的軸向應力值為常數:

又因為小尺度模型面上的某點軸向位移可以由已知的各單元節點的軸向位移{W}插值表示出來，單元確定了，形函數〔N〕就可以知道，于是有:

假設小尺度模型在連接界面上涉及到的單元總數為 Nelememt，將式(5)、(6)代入式(4)得到:

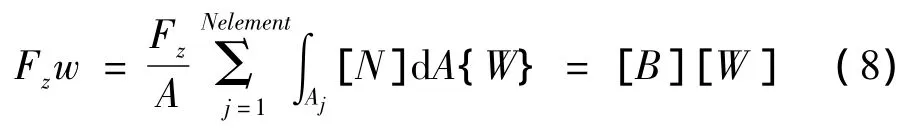
其中:Aj為小尺度模型單元j在連接面上的面積。

得到在軸向拉壓情況下的多點位移約束方程為:

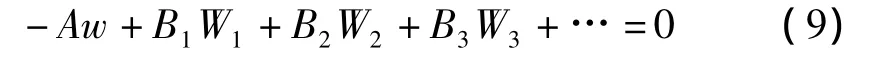
其中:Wi為在跨尺度界面上小尺度模型單元節點i沿該面法線方向上的位移，Bi為約束方程(9)式中節點位移Wi的系數。

同理，可以得出模型分別在彎矩、剪力、扭轉作用下的多點位移約束方程。這種方法是從滿足跨尺度界面應力連續性的角度出發，根據功相等導出位移約束方程，條件是要引入相應的應力公式，可以保證應力在跨尺度界面處精確傳遞，同時也要保證跨尺度界面能符合一定假設條件。

2 兩種連接方法的算例分析和比較

以一箱形截面的懸臂梁的自由端在各種方向下受力后的位移分析為例，考察上述兩種連接方法的計算效果。該懸臂梁橫截面尺寸為15 mm×12 mm，梁長為1 m。材料屬性取彈性模量為210 GPa，材料泊松比為0.3。

基于ANSYS有限元軟件，分別建立單一大尺度梁單元模型(a)，單一小尺度殼單元模型(b)和雙尺度有限元模型(c)，如圖4所示。雙尺度有限元模型將懸臂梁平均分成兩段，左邊部份為小尺度精細殼單元模型，右邊部份為大尺度梁單元模型。梁單元采用的是beam188，殼單元采用的是shell63，其中雙尺度模型在跨尺度界面上分別用上一節描述的兩種建立約束方程的單元連接方法進行跨尺度連接。

其中雙尺度有限元模型圖4(c)分別采用上述兩種單元連接方式進行跨尺度連接，即:① 根據位移協調建立位移約束方程的連接，在ANSYS中用CERIG命令，選好主從節點，即可自動建立好剛性連接的約束方程[18];② 根據應力連續建立位移約束方程的連接，需要用CE命令，輸入參與方程的位移自由度及其系數、方程常數，該系數需要自己推導并編寫相應程序。

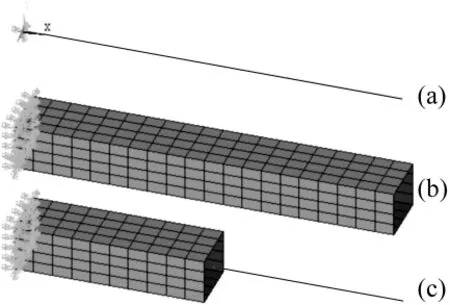
圖4 懸臂梁構件的各類有限元模型Fig.4 The cantilever beams with different finite element models

2.1 位移計算結果的比較

分別在懸臂梁自由端六個自由度方向作用載荷，值為10 kN或10 kN·m。以全由beam單元建立的梁單元模型為基準，考察采用兩種單元連接方法的雙尺度模型自由端在各種載荷作用下的位移及其與梁單元模型的相對誤差，計算結果見表1。

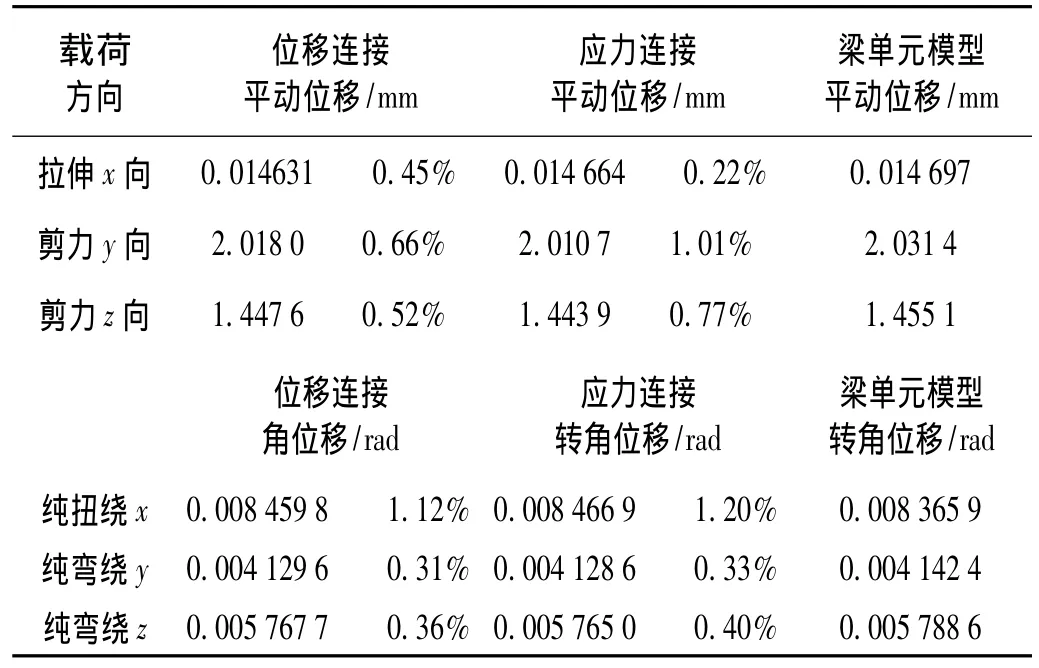
表1 多尺度模型與宏觀模型在各種載荷下位移結果的比較Tab.1 The comparisons of the displacement values got from different finite elements under different loadings

從表1中可以看出:兩種雙尺度有限元模型的位移計算結果和單一大尺度梁單元模型很近似，兩種雙尺度有限元模型之間的差別不是很大。不同于梁單元模型，由于小尺度精細模型在其固定邊界上的面內位移被限制及泊松比的存在，會對面外位移產生影響，所以含精細模型邊界的雙尺度有限元模型的位移計算結果基本要小于單一尺度梁單元模型。由此可見在進行多尺度有限元建模時，模型邊界條件的差異也是需要注意的地方。

2.2 應力計算結果的比較

為了考察雙尺度有限元模型在小尺度精細單元節點上的應力值，需要用單一小尺度殼單元模型來與這兩個采用不同跨尺度連接方法的雙尺度有限元模型做比較。在各個模型自由端處作用沿x軸正向拉力10 kN及沿y軸正向剪力10 kN，為了保持和梁單元的受力情況一致以利于比較，將作用力平均分布到自由端節點上，計算后得到的應力分布云圖見圖5，并給出殼單元模型上不同橫截面上所有殼單元節點中面的Mises應力值，見圖6。

圖5 各個模型殼單元中面的Mises應力分布圖Fig.5 The Mises stress distribution in different finite element models

從圖5可以看出三種有限元模型在精細殼單元模型部分的應力分布基本一致，下面給出精細殼單元模型部分不同橫截面上所有殼單元節點中面的Mises應力值，見圖6。

圖6 三種模型殼單元節點的Mises應力值Fig.6 The Mises stress of different finite element models in different locations

從圖5、6中可以看到，三種有限元模型在其精細部分的應力分布基本一致，模型(a)與模型(c)的應力值一直都很相近，模型(b)在跨尺度界面上的應力值較其它兩個模型相差較遠，但隨著距離跨尺度界面越來越遠，其應力值也和其它兩種模型越來越接近。這是因為模型(b)采用的是滿足界面位移協調的約束方法，忽略了小尺度精細模型在跨尺度界面上的面內位移，導致其應力值產生誤差，但根據圣維南原理，在其遠離跨尺度界面的地方，其應力值應該是比較準確的，這也符合上面的計算數據。模型(c)采用的是滿足跨尺度界面應力連續的連接方法，該方法的出發點就是要保證跨尺度界面處的應力值準確，這也符合了上面的計算結果。如圖6中所示，當橫截面距離跨尺度界面15 cm時，三種有限元模型在此處的應力值已經幾乎一致了，而此懸臂梁橫截面的最大尺寸也是15 cm，說明了在引用滿足跨尺度界面位移協調的連接方法時，跨尺度界面與所關注部位之間的過渡區尺寸最好能達到梁構件橫截面的最大尺寸。

通過前面對兩種跨尺度單元連接方法的詳細比較分析，使我們可以更好地把握對該方法的運用。綜合考慮后，滿足跨尺度界面位移協調的約束方程地建立要方面許多，且當留有適當的過度區后，我們所關心的應力值也相當精確。于是，本文的跨尺度分析方法在以后的各類計算分析中，都選用滿足跨尺度界面位移協調的節點位移約束方法進行跨尺度單元連接。

3 剛節點構件損傷多尺度分析

為了進一步考察跨尺度分析方法，在大型有限元軟件ABAQUS進行考慮材料損傷演化的結構動力響應有限元分析，將以抗震結構的典型構件——狗骨式剛節點在強動載荷下的損傷分析為例。在狗骨式剛節點的地震響應分析過程中引入材料損傷，利用UMAT子程序[19]，寫入Lemaitre應變－損傷耦合本構模型和損傷演化方程[20－21]，分析材料損傷對低周反復載荷下狗骨式剛節點抗震性能的影響及考慮材料損傷時剛節點構件的失效過程與破壞模式。建立多尺度模型，比較全實體單元的精細模型與多尺度模型的損傷分布計算結果及其計算時間，來說明多尺度模型在結構損傷計算中的可行性及其在計算效率上的優越性。

3.1 算例結構的幾何模型

作為改善鋼框架結構抗震性能的主要節點形式之一，狗骨式節點設計原理是采用削弱梁翼緣截面方式來降低梁的抗彎能力，削弱部分起到保險絲的作用，使塑性屈服在梁削弱位置出現并擴展，避免節點過早出現裂縫，相對而言等于提高了節點延性和抗彎能力。

為確定圓弧狗骨式節點的截面削弱區位置及尺寸，美國 FEMA(Federal Emergency Management Agency)推薦了該類節點的設計方法。圓弧型翼緣削弱節點的設計參數如圖7所示，b為起始削弱點距柱表面距離，c為削弱寬度，a為削弱深度。削弱部位寬度c主要由延性和剛度要求確定，削弱深度a的取值須保證最大削弱截面成為破壞控制截面，b的取值必須滿足節點的構造要求。幾何模型尺寸見表2

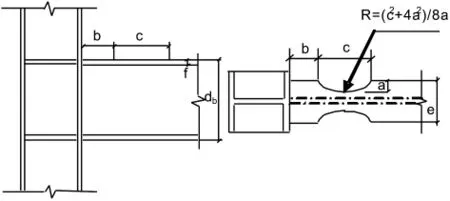
圖7 狗骨式節點幾何參數示意圖Fig.7 The physical dimensions of the dog-bone frame joint

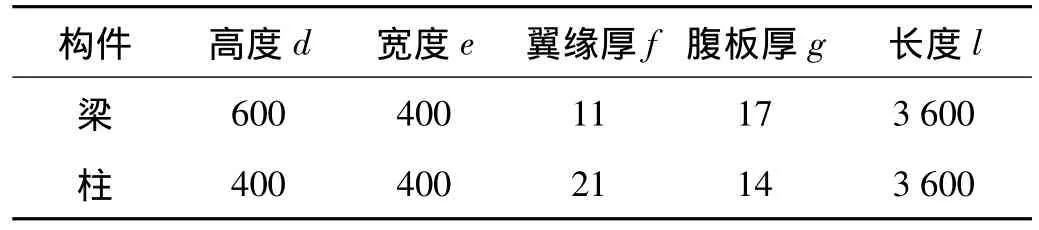
表2 鋼框架狗骨式節點梁柱截面尺寸/mmTab.2 The physical dimensions of the dog-bone frame joint/mm

在有限元模型中，柱高和梁長均取為3 600 mm。綜合圓弧形狗骨式剛節點的削弱截面尺寸要求，取a=50 mm、b=125 mm、c=450 mm、R=535 mm，節點區形狀可參照圖7。

3.2 材料損傷本構及其參數

Lemaitre彈塑性損傷耦合本構理論適用于描述金屬延性損傷特性對其應力應變關系的影響，且只需改變損傷演化方程，即可引入不同金屬材料的損傷本構方程完成計算。用彈性模量表示損傷變量時，可以應用完備形式的三維Lemaitre損傷演化動力律(10)式描述鋼材的損傷特性。

損傷演化動力律:

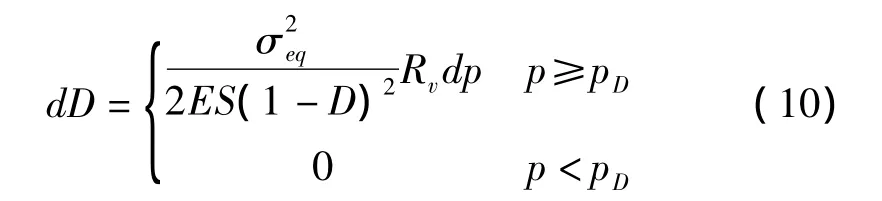
若有D=Dc，并且有，則裂紋萌生。式中的材料參數必須通過材性實驗和損傷度量來確定:D:損傷變量;S:損傷的能量強度;Pd:與材料和載荷有關的損傷門檻函數;σu:材料的極限強度;Dc:臨界損傷。

在結構分析中，假設當局部應變大于材料極限應變時該處材料達到極限強度，隨后該處材料會發生塑性流動變形和頸縮破壞;當材料達到極限應變時，損傷也達到其極限值。本文選取了Von Mises屈服準則和混合強化模式，考慮Q235鋼的材性實驗以及其塑性硬化規律實驗結果，可以得到彈塑性材料性能指標:彈性模量E=200 GPa，泊松比 v=0.3，屈服強度 σy=235 MPa，隨動強化模量Hk=1 100 MPa，混合強化系數h=0.2。除了彈塑性材料性能指標外，還需要通過材料的損傷度量實驗確定Lemaitre損傷演化方程中的材料常數。現有資料中可以將Q235鋼的損傷應變門檻值取為εpd≈0.01，將結果推廣到三維條件下，可以認為累積塑性應變值達到0.01時損傷起始。綜合宋振森的損傷實驗結果和Lemaitre理論中損傷能量強度S的計算方法，考慮Q235鋼達到強度極限時塑性應變極值為εu=0.15可以確定Q235鋼臨界損傷值為D1C，其損傷能量強度 S=0.281 MPa[22－24]。

3.3 UMAT子程序實現流程

ABAQUS中用戶材料子程序UMAT的開發主要解決兩方面問題:本構模型建立和積分算法選擇。本文在UMAT中應用完全隱式向后Euler法的徑向返回方法，考慮了平衡迭代的收斂和計算結果的正確性，用程序形式寫出了Lemaitre損傷塑性理論(圖8)。結構的彈塑性行為與加載以及變形的歷史有關，一般使用增量載荷法計算，對每一載荷增量，將彈塑性方程分步線性化，從而使得彈塑性分析這一非線性問題分解為一系列線性問題。

UMAT子程序的主要功能是根據程序定義的材料本構方程，由主程序傳入的應變增量求解應力增量，更新積分點處的應力應變狀態，提供雅克比矩陣(Jacobian)給ABAQUS主程序以形成下次迭代時的單元切線剛度矩陣和結構整體剛度矩陣。

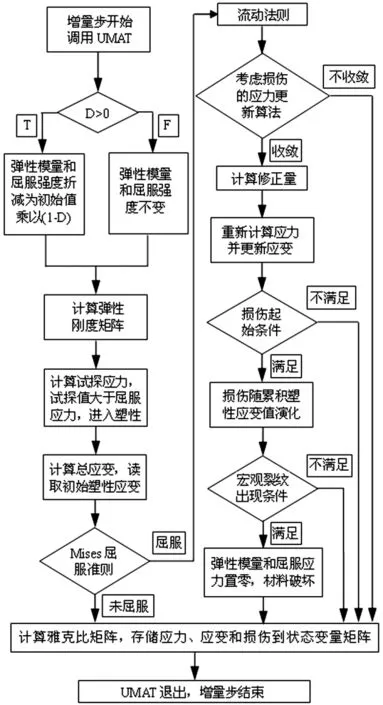
圖8 應用UMAT子程序實現損傷本構描述的流程圖Fig.8 The flow chart of introducing meso-damage equation and coupled calculation of stresses with damage evolution in the subroutine UMAT

3.4 有限元模型的建立及結果

對于單一小尺度實體單元模型，考慮各類型單元的特性和本文進行的彈塑性損傷分析要求，為最大程度地保證計算準確性，選用實體單元C3D20R進行計算。對于多尺度模型，把局部薄弱易損傷區域用實體單元C3D20R模擬，通過上一節中的計算分析可知，為了保證缺陷部位計算的精度，多尺度模型用實體單元模擬的精細部分在跨尺度界面和薄弱部位之間要給予適當的過渡區域，該區域的長度最好能取梁橫截面的最大尺寸。由于應用損傷理論來分析模型的缺陷部位，所以要保證在缺陷部位的實體單元的特征尺寸在1～5 mm范圍內。多尺度模型的其它非重要部分采用梁單元B31來模擬，梁單元模擬部分由于一直處于線彈性階段，所以采用線彈性本構關系。多尺度有限元模型的跨尺度界面采用耦合的方法將兩種尺度模型連接起來，耦合類型為kinematic，該類型耦合方法與本文列舉的滿足跨尺度界面位移協調的約束方法類似。

有限元模型(a)共有19 733個節點，實體單元C3D20R共有2 964個，有限元模型(b)共有12 497個節點，其中實體單元C3D20R共有1 920個。所以，多尺度模型相對于單一小尺度精細模型節省了近1/3的節點數量和單元數量。

邊界條件及加載條件:見圖9，在剛節點中柱底面的x、y、z方向設置位移約束，在柱頂面x、z方向設置位移約束，在梁端控制y方向位移。首先通過單向載荷下剛節點的響應分析，可以確定該削弱截面處開始進入塑性時，y方向的屈服位移Δy=0.025 m。

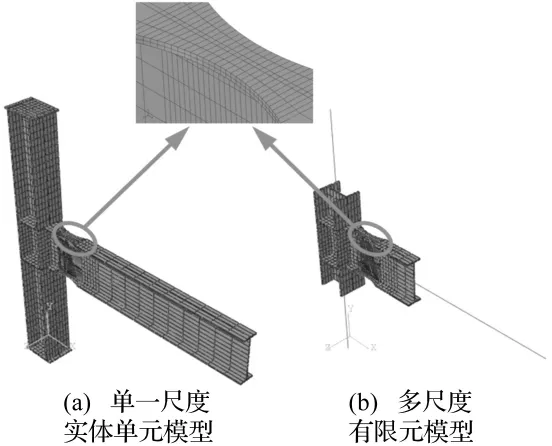
圖9 狗骨式節點有限元模型及其薄弱處的單元網格Fig.9 The finite element model of the dog-bone frame joint

考慮了《建筑抗震試驗方法規程》(JGJ101－96)相關要求，采用ECCS完全加載制度，加載時梁端位移按以下方式進行:

要確定節點關鍵截面處梁翼緣全截面材料的累積塑性應變是否達到了極限值，可以根據文獻[23]的實驗結果，在剛節點構件損傷過程和抗震性能分析中，認為梁削弱處全截面累積塑性應變值達到0.15時，構件失去承載能力;梁削弱處全截面累積塑性應變值達到0.25時，構件發生破壞。剛節點在低周反復加載的計算分析過程中，每一周加載到極限值時所用的分析時間設為1 s。經過計算，加載過程中當Δ=2Δ+y(t=5 s時刻)開始，累積塑性應變達到損傷起始值，剛節點梁部分削弱程度最大截面翼緣處的材料損傷開始萌生和演化;當加載位移由3Δy增至4Δy后，梁削弱處全截面累積塑性應變達到極限值，載荷作用下截面削弱處較長梁段材料均進入塑性并產生不同程度的損傷。于是，剛節點梁端作用的位移低周反復載荷在第一次達到4Δ+y時停止，一共循環了6周半，總共分析時間為13 s。比較單一小尺度實體單元模型與多尺度有限元模型在加載到13 s時，兩種有限元模型在局部處的損傷分布，見圖10。

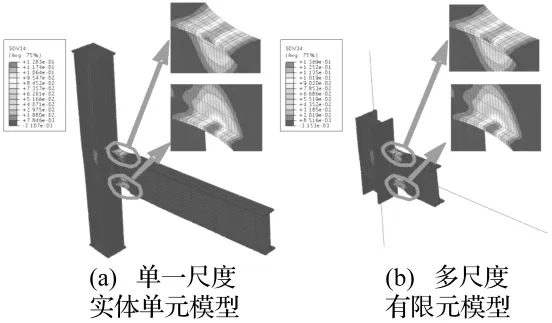
圖10 采用兩種模型計算得到的損傷分布狀況Fig.10 The damage distribution on vulnerable areas in two different finite element models

從圖10中可見兩種模型計算得到的損傷分布基本一致，剛節點梁部分削弱程度最大截面的翼緣外側的損傷量最大，且表現出此時狗骨式剛節點的材料損傷主要分布在梁削弱截面處，翼緣削弱程度越大則損傷量越大。為了比較兩種狗骨式剛節點有限元模型加載各階段在梁截面削弱處損傷演化的具體差異，從加載時間的第5 s、剛出現損傷開始，列出模型(a)、(b)在各時刻的損傷最大值，也即翼緣削弱程度最大處的損傷值，見表3。

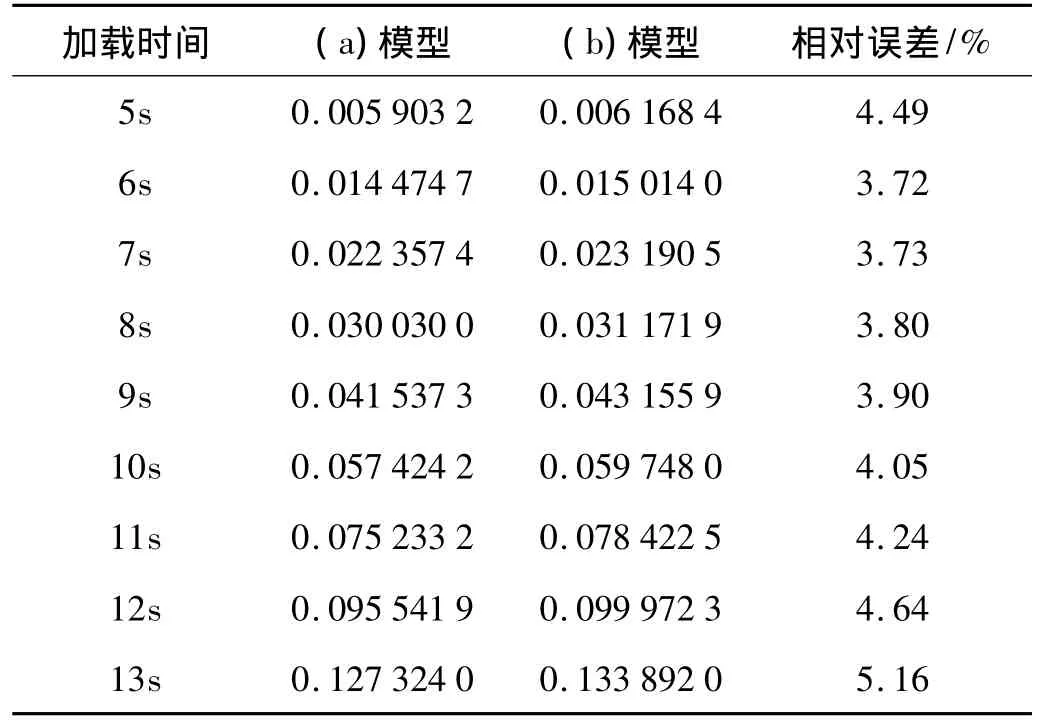
表3 兩種模型計算得到的損傷值Tab.3 The comparisons of damage values got from two different finite element models

從上表可以得到，兩種模型在加載過程中，損傷增量越來越大，損傷演化速度加快;除去損傷剛開始不久5 s時的損傷值，兩種模型相同位置處損傷值之間的相對誤差也越來越大，這是可能是由于載荷幅值不斷加大以及計算誤差不斷累積造成的。盡管兩種模型之間存在一定的計算誤差，多尺度有限元模型依然能夠準確地估計狗骨式剛節點薄弱區域的損傷起始時間，準確地反映薄弱區域的損傷演化及分布情況。在加載的最后時刻，兩類有限元模型在剛節點梁削弱處的損傷值誤差達到最大，但基本可以確定是在剛進入4Δ+y位移加載循環時達到承載極限。

在同一臺電腦上，(a)、(b)兩種模型的計算時間比較:

(a) 模型的CPU運行時間:2 353.5 s

(b) 模型的CPU運行時間:1 525.1 s

從對比可以看出，(b)模型的CPU運行時間相對于(a)模型節省了近1/3的時間，大大提高了計算效率。通過此次狗骨式剛節點考慮材料損傷演化的計算分析對比，多尺度有限元模型總體上的損傷分布情況基本和單一尺度實體單元模型一致且計算結果相差不大。因此，可以認為在進行強載荷作用下鋼構件的動力響應和損傷分析時，引用跨尺度分析方法不僅可行而且可以提高計算效率。

4 鋼桁架結構的損傷跨尺度分析

為了進一步探索跨尺度分析方法在結構損傷分析中的應用，并盡量避免由于結構模型復雜而對計算結果準確性造成的不可預知影響，本文分析了具有代表性的某大跨懸索橋鋼箱梁縱向加勁鋼桁架結構，分別建立單一小尺度精細單元模型和多尺度有限元模型并對比它們的靜力響應、動力特性以及強載荷下的非線性動力響應和計算效率。該結構中的構件截面特點和尺寸都比較規則，也具有一定的工程應用典型性。

在大跨橋梁結構中，其鋼箱梁結構形式非常有代表性，選取其中縱向加勁桁架結構的典型標準段按照1∶5的比例制作了縮尺實驗結構試樣。縮尺結構試樣的主要結構尺寸、焊縫形式、加工工藝等均以與原橋鋼箱梁縱向加勁桁架原型實際相似為準則，材料為普通Q235鋼，整個模型高1.32 m，長4.2 m，焊接鋼桁架試驗系統實體圖見圖11。

圖11 焊接鋼桁架結構試驗系統實體圖Fig.11 The testing system of the welding steel truss

4.1 多尺度有限元模型的建立

在整個剛桁架結構中，有很多地方是符合梁單元特性的，且在加載過程中始終不會有損傷產生，屬于不需要關注的部位。于是，針對這樣的情況可以選擇跨尺度分析方法來模擬整個剛桁架結構，將可能發生損傷的局部缺陷部位用適用于小尺度損傷分析的實體單元來模擬，不發生損傷且符合梁單元特性的部分用適用于大尺度分析的梁單元來模擬。

根據對跨尺度界面的要求和圣維南原理，小尺度局部節點區域在應力集中區域和跨尺度界面之間要留有一定的過渡區域，以防止由于局部應力集中對跨尺度界面產生影響，引起計算結果產生誤差;在本例中，對于易發生損傷的梁附近留有沿梁長方向0.15 m的過渡區域(0.15 m為該加勁鋼桁架結構梁的最大尺寸)，為了保險起見，對于沒有發生損傷的節點區域也沿梁長方向留有0.1 m的過渡區域，以保證模型的計算精度。建立好后的多尺度有限元模型包含了59 980個節點，8 412個C3D20R單元。沒有采用跨尺度分析方法的單一小尺度實體單元模型包含了72 656個節點，10 406個C3D20R單元，見圖12。

圖12 鋼桁架結構的兩種有限元模型Fig.12 Two different finite element models of the steel truss

4.2 實驗驗證及對比

為了對比本文所建的單一小尺度實體單元模型和多尺度有限元模型、并將它們與實驗數據做比較，驗證這兩種模型的準確性，根據實驗工況加載(見圖11)，計算了在200 kN載荷作用下，兩種模型在圖13中測點位置上(虛線位置)的應變分布特性。

計算后，得到鋼桁架結構在200 kN載荷作用下，(a)、(b)兩種模型與應變分布實驗在測點位置的應變值分布，見圖14。

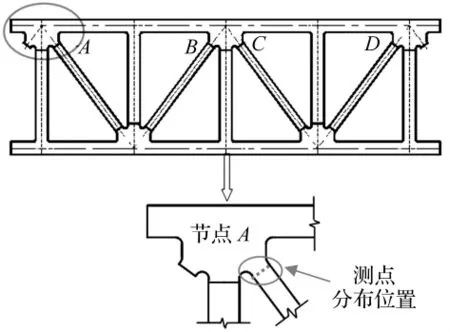
圖13 應變分布實驗測量位置Fig.13 The locations of the strain distribution test

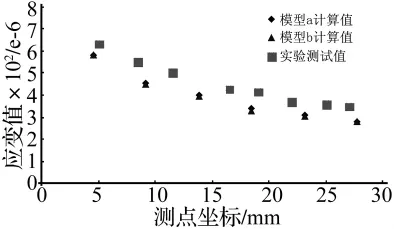
圖14 兩種有限元模型與應變分布實驗在測點位置處的應變值分布Fig.14 The strain values got from the finite element models and the test in different locations

從圖14中，發現單元小尺度實體單元模型與多尺度有限元模型之間的計算結果差別很小，可以證明多尺度有限元模型可以替代單一小尺度實體單元模型進行靜載荷下關注局部熱點應力、應變分布的計算分析。有限元模型計算得到的應變值與實驗測得的應變值相對于測點位置的變化趨勢是十分吻合的。但是，數值模擬得到的結果與實驗結果相比整體偏小，這主要是由于數值模型及載荷、位移邊界條件都無法還原真實情況造成的。

分別用單一小尺度實體單元模型和多尺度有限元模型計算鋼桁架結構的整體一階彎曲振型頻率和局部斜向構件一階彎曲振型頻率并做比較(見圖15)，考察多尺度模型替代單一尺度模型進行動力特性分析的可行性。再用兩種模型的數值模擬結果來對比實驗測試結果(見表4)。

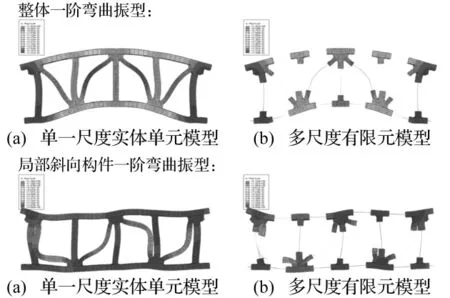
圖15 加勁鋼桁架結構兩種有限元模型的振型圖對比Fig.15 The vibration modes of the two different steel truss finite element models

表4 鋼桁架結構實驗測試和兩種有限元模型模擬的固有頻率對比Tab.4 The comparisons of steel truss natural frequency got from two different finite element models and the test

從圖15的兩種模型振型圖對比和表4的各項數值可以看出，多尺度有限元模型和單一小尺度實體單元模型的相似度很高，雖然前者相對于后者使用了大量梁單元來替代實體單元，但是通過結構整體一階彎曲振型及它們頻率值的對比，可以證明兩種模型的質量及剛度分布一致，通過局部斜向構件一階彎曲振型及它們的頻率值的對比，可以證明多尺度有限元模型可以替代單一尺度實體單元模型識別結構局部損傷狀態。通過對應振型固有頻率的數值計算結果與實驗測試結果的對比，發現它們之間的相對誤差均在10%以內，兩種結果比較接近，可以認為單一小尺度實體單元模型和多尺度有限元模型計算出的結構動力特性比較符合實際情況。

4.3 鋼桁架結構的動力響應與損傷跨尺度分析

為分析低周反復載荷下鋼桁架結構的損傷失效過程，根據本文3.3節中介紹的用于抗震分析的ECCS完全加載制度施加位移控制載荷，當結構危險點處累積塑性應變達到極限值而導致該位置處材料失去承載能力時結束加載。載荷施加方式與模型邊界條件如圖12所示，鋼桁架兩邊底部的節點施加固定約束，位移控制載荷施加在鋼桁架中部的頂端節點、腹桿中部及底端節點三處。

通過單向載荷下鋼結構的響應分析，可以確定鋼桁架結構節點薄弱區域開始進入塑性時，其加載方向y方向的屈服位移Δy=0.002 m。在進行低周反復載荷下鋼桁架結構的動力響應與損傷分析時，循環一周的時間仍按2 s計，載荷分析步時間初設為0.05 s。

通過計算，鋼桁架單一小尺度實體單元模型在位移載荷第一次達到4Δ+y時，其最大累積塑性應變達到0.15，該位置處材料失去承載能力，加載停止，總共加載過程歷經時間13 s，269個載荷分析步。鋼桁架多尺度有限元模型在位移載荷接近4Δ+y時(12.96 s)，其最大累積塑性應變達到0.15，為了便于與單一小尺度實體單元模型對比，也計算到13 s，總共經過了268個載荷分析步。加載完成后，對比整體結構上所有的損傷區域，損傷值比較大的區域都出現在鋼桁架結構的下端。給出兩種模型最后時刻危險點(塑性和損傷累積程度最高處)區域的損傷分布情況(見圖16)及在危險點處各個加載時刻的損傷值(見表5)。

通過上面的對比可以發現兩種模型在最后時刻的損傷區分布一致，各個加載時刻的損傷值也十分接近。雖然兩者之間的計算結果會隨著加載過程不斷增大，但它們最終的誤差不大，且多尺度有限元模型估計的損傷起始時刻及危險點處材料的承載力失效時刻都和單一小尺度實體單元模型估計的幾乎一致。此次計算，單一小尺度實體單元模型一共經歷了269個載荷分析步、6 656.9 s的計算時間，多尺度有限元模型一共經歷了268個載荷分析步、4 120.3 s的計算時間。跨尺度分析方法在此次模擬地震載荷下的結構動力響應與損傷分析中節省了38%的計算時間，體現出了極大的優越性。

表5 兩種模型計算得到的危險點處損傷值Tab.5 The comparisons of damage values got from two different finite element models

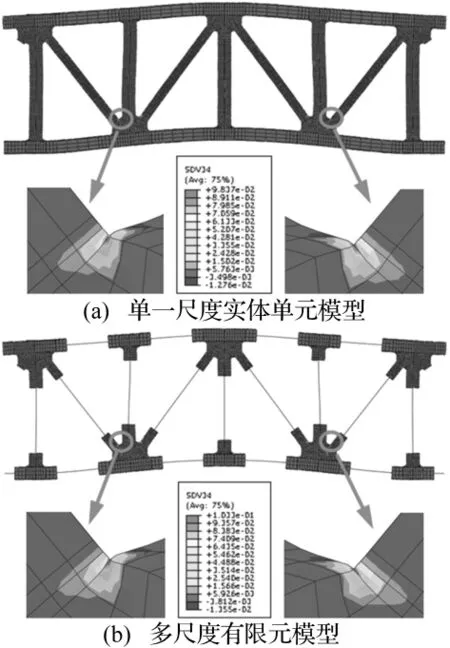
圖16 低周反復載荷完成后鋼桁架有限元模型在危險點處的損傷區分布Fig.16 The damage distribution in the steel truss under ECCS cyclic loading

5 結論

由本文的研究可得到以下結論:

(1)從應用角度考慮，滿足跨尺度界面位移協調的約束方程的建立過程比較簡單、易于實現程序化，而滿足跨尺度界面應力協調的約束方程的建立過程比較繁瑣、實現起來比較麻煩。且兩種跨尺度界面連接方法成立的條件都是是跨尺度界面所在位置要滿足彈性小變形以及相關的梁單元假設，因此，跨尺度界面必須遠離塑性區或者損傷區才能應用于損傷非線性分析。

(2)狗骨式剛節點的多尺度有限元模型與單一小尺度實體單元模型在多步計算以后，其損傷累積值差別不大，且各階段損傷分布基本一致。通過兩種模型的計算時間比較，多尺度模型替代單一小尺度精細模型可大大提高計算效率。雖然本文分析的構件的計算規模較小，但可以預見，所分析的結構計算規模越大，可節省的計算時間就會越多。

(3)本文建立的鋼桁架結構多尺度有限元模型是比較成功的，在靜動力分析中都能很好的近似單一小尺度實體單元模型，且都接近實驗測試結果，具有較高的可信性。文中的跨尺度分析方法在結構動力響應和損傷分析中的應用，實現了強載荷下由材料損傷劣化引起構件和結構局部失效的模擬，更準確地描述了強動載荷作用下結構中由于材料損傷演化導致結構的非線性響應和局部失效的過程，進一步解釋了強動載荷下發生的從材料損傷到構件節點失效再到結構破壞的機理。而且應用該跨尺度分析方法建模比較方便，且可以提高分析效率，在不失精度的前提下，體現了極大的優越性和應用前景。

[1]吳佰建，李兆霞，湯可可.大型土木結構多尺度模擬與損傷分析—從材料多尺度力學到結構多尺度力學[J].力學進展，2007，37(3):321 －336.

[2]李兆霞，孫正華，郭 力，等.結構損傷一致多尺度模擬和分析方法[J].東南大學學報(自然科學版)，2007，37(2):251－260.

[3]李兆霞，王 瀅，吳佰建，等.橋梁結構劣化與損傷過程的多尺度分析方法及其應用[J].固體力學學報，2010，31(6):731－756.

[4]孫正華，李兆霞，陳鴻天，等.考慮局部細節特性的結構多尺度模擬方法研究[J].特種結構，2007.3，24(1):71－75.

[5]Monaghan D J，Doherty I W，McCourt D，et al.Coupling 1D beam to 3D bodies[C]. 7th InternationalMeshing Roundtable. Sandia National Laboratories， Dearborn，Michigan，1998:285－293.

[6]McCune R W，Armstrong C G，Robinson D J.Mixed dimensionalcoupling in finite element models[J].International Journal for Numerical Methods in Engineering，2002，49:725－750.

[7]Shim K W，Monaghan D J， Armstrong C G. Mixed dimensional coupling in finite element stress analysis[J].Engineering with Computers，2002，18:241 －251.

[8]Surana K S.Transition finite elements for axisymmetric stress analysis[J].International Journal for Numerical Methods in Engineering，1980，15:809 －832.

[9]Surana K S.Transition finite element for three dimensional stress analysis[J].International Journal for Numerical Methods in Engineering，1980，15:991 1020.

[10]Garusi E，Tralli A.A hybrid stress-assumed transition element for solid-to-beam and plate-to-beam connections[J].Computers and Structures，2002，80:105 －115.

[11]Kim H S，Hong S M.Formulation of transition elements for the analysis of coupled wall structures[J].Computers and Structures，1995，57(2):333－344.

[12]McCune R W，Armstrong C G，Robinson D J.Mixed dimensionalcoupling in finite elementmodels [J].International Journal for Numerical Methods in Engineering，2000，49:725－750.

[13]Wenzel M.On dimensional adaptivity for mixed beam-shellstructures[J].PAMM-Proc.Appl.Math.Mech，2004，4:382－383.

[14]Chavan K S，Wriggers P.Consistent coupling of beam and shell models for thermo-elastic analysis[J].International Journal for Numerical Methods in Engineering，2004，59:1861－1878.

[15]王勖成.有限單元法[M].北京:清華大學出版社，2003.

[16]陸新征，林旭川，葉列平.多尺度有限元建模方法及其應用[J].華中科技大學學報(城市科學版)，2008，25(4):76－79.

[17]林旭川，陸新征，葉列平.鋼－混凝土混合框架結構多尺度分析及其建模方法[J].計算力學學報，2010，27(3):469－475.

[18]ANSYS Release 10.0，ANSYS Inc.，2007.

[19]ABAQUS Theory Manual[M].ABAQUS，Inc，2006.

[20]Lemaitre J.A Course on damage mechanics[M].Spring-Verlag，1992.

[21]Lemaitre J，Desmorat R.Engineering damage mechanics[M].Springer-Verlag，2005.

[22]羅邦富，魏明鐘，沈祖炎.鋼結構設計手冊(第二版)[M].北京:中國建筑工業出版社，1989.

[23]張 莉.鋼結構剛性梁柱節點抗震性能的研究[D].天津:天津大學，2004.

[24]宋振森.剛性鋼框架梁柱連接在地震作用下的累積損傷破壞機理及抗震設計對策[D].西安:西安建筑科技大學，2001.