初中數學變式教學策略研究

☉江蘇省海安縣李堡鎮初級中學 呂廣春

初中數學變式教學策略研究

☉江蘇省海安縣李堡鎮初級中學 呂廣春

學習本身就是對事物的本質屬性進行認識的過程，在這一過程中，我們常常會被一些事物的非屬性而迷惑.所謂的變式即變換事物的非本質特征而保持本質特征的不變，或變換事物的本質特征而保持某些非本質特征的不變，但這些變換所得到的不同表現形式和原有事物之間保持一定的相似性，這些變換所得到的不同形式就是事物的變式.在數學教學中，教師通過改變問題中的一些附加條件來引導學生認識數學知識的教學方式即為變式教學.

初中數學 變式教學 策略

在新課改下，教學所要做的并不是傳統的讓學生學會解題，學會在考試中獲得高分，更多的是以學生的能力培養為重.《初中數學新課程標準》中也明確指出“數學課堂能使學生掌握必備的基礎知識和基本技能；培養學生的的抽象思維和推理能力；培養學生的創新意識和實踐能力……”變式教學靈活多變，根據相關研究人員研究證實，變式教學不僅有利于提高學生學習效率，促進思維能力發展，對提高課堂教學效率和創新能力等都有積極意義.本文就初中數學變式教學中的基本概念、數學命題、數學語言和問題解決的變式教學策略作簡要分析.

一、基本概念變式教學策略

在初中數學中，基本概念變式教學主要為概念的引入變式，深化變式和鞏固變式幾種.以概念深化變式教學為例，初中數學中，對概念的掌握是重點，數學知識的建構都以概念為基礎.因此，在課堂教學中加強學生對概念的深化理解將有效地提高學生解決數學問題的能力.概念深化變式注重引導學生探究概念的等價形式或變式含義，同時對等價形式及變式含義的應用進行探究，從而加強對概念的理解.

如在一次函數的教學中，在通過對一次函數的定義（y=kx+b，k≠0，且k、b為常數）進行學習后，為讓學生充分理解定義中自變量x，系數k、b的含義，教師引導學生進行如下分類探究：

（1）如果設b=0，定義中其他數量不變，函數還是一次函數嗎？如果不是，那是什么函數？

（2）如果k=0，定義中其他數量不變，函數還是一次函數嗎？如果不是，那是什么函數？

（3）如果k=0，b=0，定義中其他數量不變又將是什么函數？

（4）在定義中，x的指數是多少？如果把指數變為2，它又是什么函數？

通過分類探討，學生對一次函數有了更清晰的認識，對其中的自變量，系數的含義的理解也更為深刻了.

二、數學命題變式教學策略

數學中的公式、定理的推導、證明方法等都有一定規律可循，通過對它們的探索，能培養學生解決問題的系統思維，對利用數學知識來解決問題具有積極意義.

以定理、公式的多證變式教學為例，教學中，教師可為學生提供多種定理的證明方法，讓學生在思考的基礎上去學習他人的證明方法.如“勾股定理”的證明.定理為在直角三角形中，兩條直角邊的平方和等于斜邊的平方.已知：直角三角形的兩直角邊的長分別是a、b，斜邊長為c.求證a2+b2=c2.

圖1

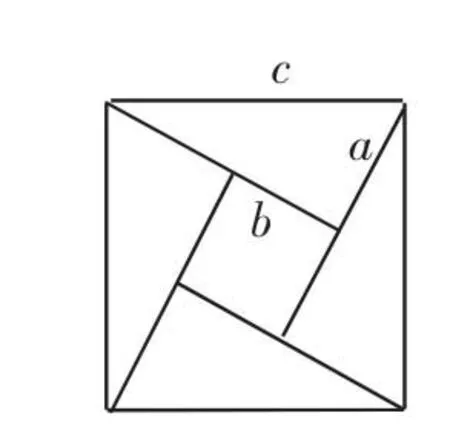
圖2

證明：如圖1中，邊長為a，b的兩個正方形連在一起，S=a2+b2.圖2可由四個全等直角三角形和一個小正方形組成.若把其中的兩個三角形移到圖2中，就會得到一個邊長為c的正方形，面積為c2，由此可得到a2+b2=c2.上述證明方法即我國古代趙爽的證明方法.

此外教師也可給學生介紹鄒元治證明、美國總統Garfield證明、梅文鼎證明、項明達證明、歐幾里得證明等多種證明方法，讓學生在多種證明方法中找到共性，從而獲得對“勾股定理”的理解.

三、數學語言變式教學策略

數學教學是引導學生利用數學語言來描述生活的過程，數學語言變式是實現概念、命題等文字、圖形、符號之間的相互轉化，從而培養學生理解能力的變式教學.在初中數學教學中，教師一方面根據文字語言來進行圖形語言描述，再轉化為符號語言，要將三種語言結合起來，讓學生在轉化中掌握共性.如平行線性質的定理：

文字語言描述為：兩條直線平行（教師邊描述邊畫兩條直線或幻燈片展示），內錯角相等（教師要指著相應的內錯角來說明）；

圖形語言描述：如圖3；

符號語言描述為：

因為AB∥CD，所以∠AEF=∠EFD.

另一方面，教師要引導學生在做題、練習、課堂討論中學會不同數學語言之間的轉化，如一個同學以文字語言進行描述，另一個同學進行圖形符號語言描述.

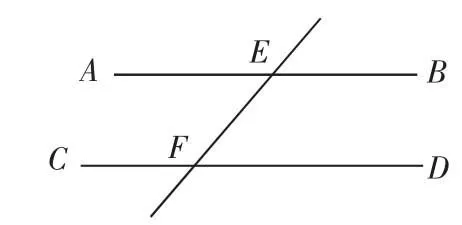
圖3

四、問題解決變式教學策略

問題解決變式教學是數學變式教學中最復雜的，其中包含的不僅有代數知識，更有幾何知識，而且方式多變，隨著條件的改變，變式的形式變化也多樣.但從另一個角度來說，這種變化更有利于對學生解決問題能力的培養.在初中數學中常見的問題解決變式主要為一題多解（證）變式、一題多變變式、多題一解（一法多用）變式、一題多用變式四大類.

以一題多用為例，如已知9x=33，求x.在初中階段，只要求能化同底并且合并化簡后是二項的指數方程.解題時，兩項分居等號兩邊，如果它們同號，則取兩邊的指數相等，解之便得到x=.化底時，宜取質數的一次冪為底，或其他盡可能小的數為底.這題的解法可以用于多道同類型的題.

應該說，在初中數學教學中進行變式教學是大有必要的，特別是在社會發展中對學生能力要求不斷加強的情況下，以變式來提高學生的能力，對促進其終身發展意義重大.