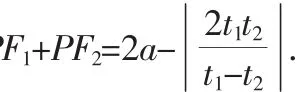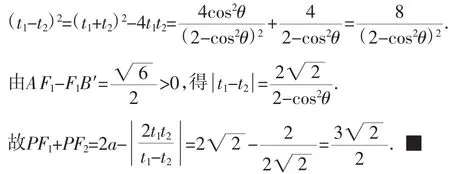2012年高考數學江蘇卷解析幾何題別解

☉江西省贛縣中學南校區 朱紅喜

（1）求橢圓的方程；

（2）設A，B是橢圓上位于x軸上方的兩點，且直線AF1與直線BF2平行，AF2與BF1交于點P.

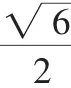
（ii）求證：PF1+PF2是定值.

（2）（i）如圖1，設點B關于原點O的對稱點為B′，連接F1B′，則四邊形BF1B′F2為平行四邊形.由AF1平行BF2，得A、F1、B′三點共線.

解法1：設A（x1，y1），B′（x2，y2）.由橢圓的焦半徑公式知

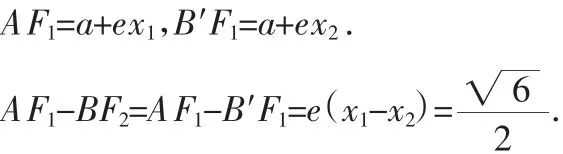
故x1-x2=，也因此知AB′的斜率存在且大于0.

設其斜率為k，則AB′的方程為y=k（x+1）.

整理得12k4+4k2-5=0，

解法2： 設F1為極點，F1F2所在直線為極軸，∠F2F1A=θ，AF1=ρ1，B′F1=ρ2，則由圓錐曲線的統一極坐標方程得

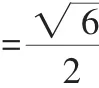
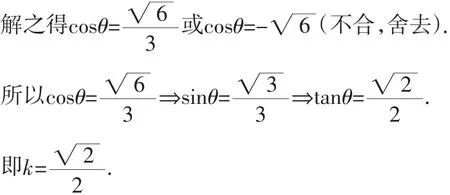
（2）（ii）解法1：由（2）（i）中解法2中的圓錐曲線統一極坐標方程，