例談從二次函數(shù)中培養(yǎng)學生的直覺思維

●駱銀海 (牌頭中學 浙江諸暨 311825)

數(shù)學思維可以分為邏輯思維和直覺思維，邏輯思維用于證明，直覺思維用于發(fā)明.新課標十分強調(diào)學生創(chuàng)新意識與創(chuàng)新能力的培養(yǎng)，直覺思維是數(shù)學創(chuàng)造與創(chuàng)新的基礎.因此，如何培養(yǎng)學生的數(shù)學直覺思維至關重要.從解題教學來看，數(shù)學直覺思維也可理解為一看到題目時的題感，題感在一定程度上是可以后天培養(yǎng)的，每個人的數(shù)學直覺通過訓練可以不斷提高.

二次函數(shù)作為中學生應用最廣泛的初等函數(shù)，也是最簡單的非線性函數(shù)，具有許多優(yōu)美的性質(zhì)，是數(shù)學命題者感興趣的考點之一.試題中背景設計之精巧、過程之流利、答案之美妙常引起師生的共鳴.筆者有幸參與了諸暨市說題展示和浙江省數(shù)學教師教學能力評比與觀摩活動，頗有體會：在解決二次函數(shù)問題中可大力培養(yǎng)學生的直覺思維，也就是說增強學生的題感，迅速獲得接近正確答案的思路和方法.現(xiàn)舉例如下：

例1 已知函數(shù)f(x)=|x2-2x-3|，若x2＞x1＞1且f(x1)=f(x2)，求x1+x2的取值范圍.

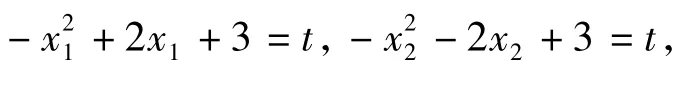
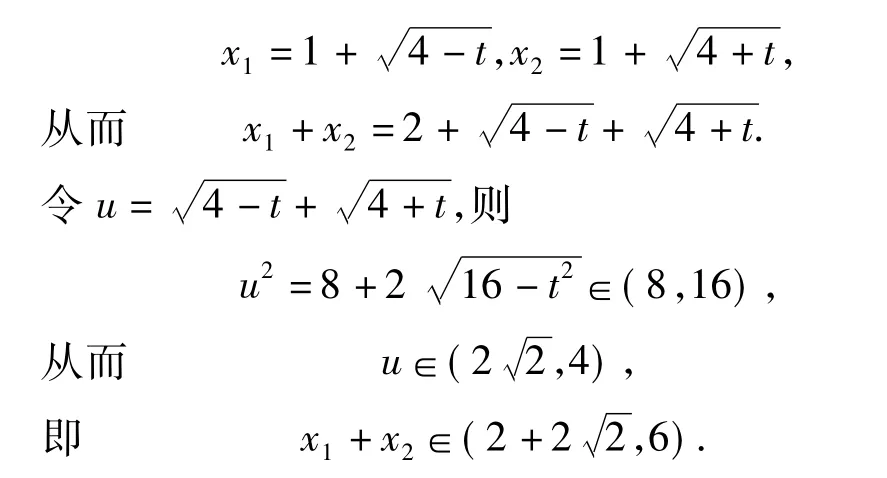
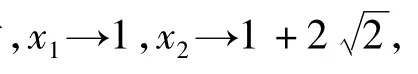
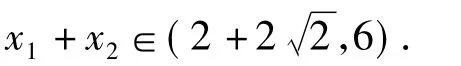
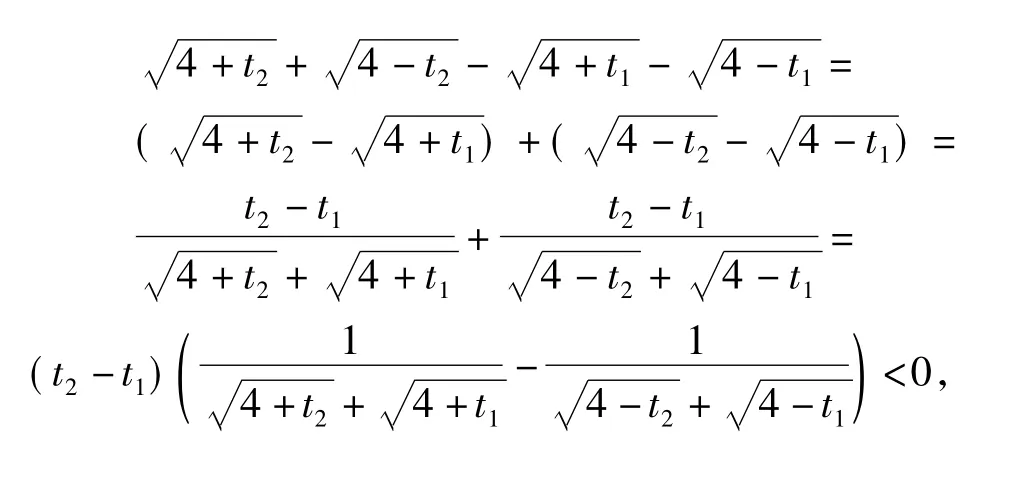
反思 本題是諸暨市高三數(shù)學二模考試試題，正確率不高，有些同學做了很長時間也沒做對，有些同學一拿到題目，題感較好，馬上想到：是否存在2個極端位置，很快就有了答案.可見，數(shù)學直覺思維活動在時間上表現(xiàn)為快速性，在過程上表現(xiàn)為跳躍性，在形式上表現(xiàn)為簡約性，簡約美體現(xiàn)了數(shù)學的本質(zhì).直覺思維是一瞬間的思維火花，是長期積累的一種升華，是思維者的靈感和頓悟，是思維過程的高度簡化.

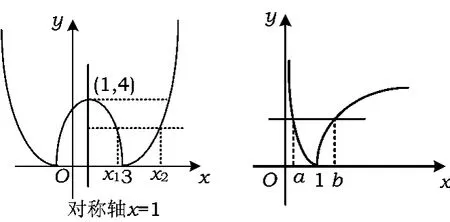
圖1 圖2

不僅僅在二次函數(shù)背景中可考慮直覺思維，類似地，在對數(shù)函數(shù)背景中也如出一轍.

2010年全國數(shù)學高考理科試題第10題是這樣設計的：

例2 已知函數(shù)F(x)=|lgx|，若0＜a＜b，且f(a)=f(b)，則a+2b的取值范圍是 ( )

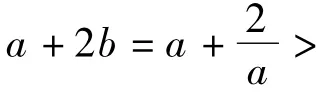
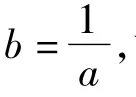
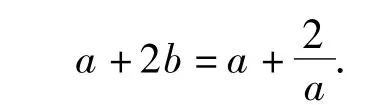
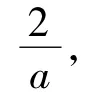
直覺思維培養(yǎng) 顯然a+2b→+∞.若能考慮到a+2b的最小值是當f(a)=f(b)→0時取到，再結合簡單的證明，那解題就變得既快又準，可以體會到直覺思維帶來的好處.

例3 設t為常數(shù)，函數(shù)f(x)=|x2-2x-t|在區(qū)間［0，3］上的最大值為2，求 t的值.

(2008年浙江省數(shù)學高考理科試題)

分析由函數(shù)g(x)=x2-2x-t的對稱軸是x=1且 g(0)=g(2)=-t，可得 f(0)=f(2).分析可知，f(x)在區(qū)間［0，3］上的最大值是f(1)或f(3).

若 f(1)≥f(3)，則

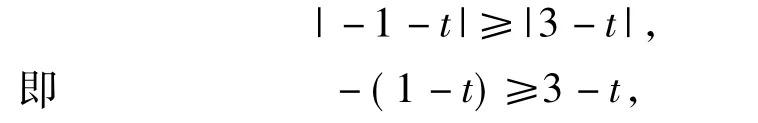
從而當t≥1時，-(-1-t)=2，解得t=1;若 f(3)≥f(1)，則

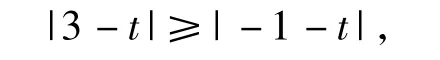
從而當 t≤1 時，|3-t|=2，解得 t=1.

綜上所述，t=1.

直覺思維培養(yǎng) 本題是在二次函數(shù)的基礎上加了絕對值函數(shù)，-t實質(zhì)是函數(shù)x2-2x的上下平移.結合導數(shù)知識fmax(x)=max{端點值，極值}，由于對稱軸x=1在已知的區(qū)間內(nèi)，因此翻折后無論產(chǎn)生怎么樣的形狀，f(x)取到的最大值一定產(chǎn)生于端點值f(0)，f(3)及極值f(1)中，即

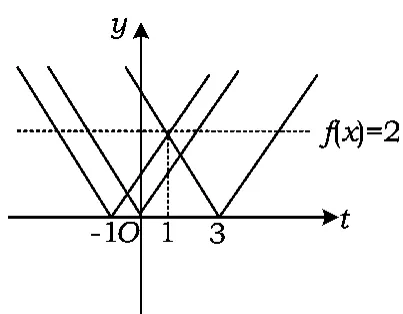
圖3

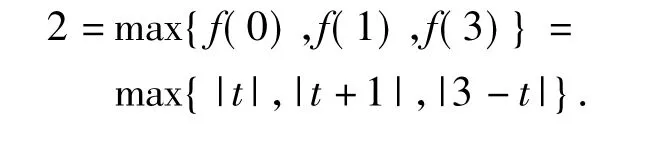
如圖3，當f(x)=2時，由直覺思維知，t=1滿足題意.

反思 直覺思維是基于研究對象的整體把握，不專于細節(jié)的推敲，是思維的大手筆，從而使認知結構向外擴展，因此直覺思維具有反常規(guī)的獨創(chuàng)性.

例4 已知二次函數(shù) f(x)=ax2+bx+c，a∈N*，c≥1，a+b=c≥1 且方程 ax2+bx+c=0 有2個小于1的不等正根，求a的最小值.

解法1 如圖4，由根的分布知

由b2-4ac＞0得

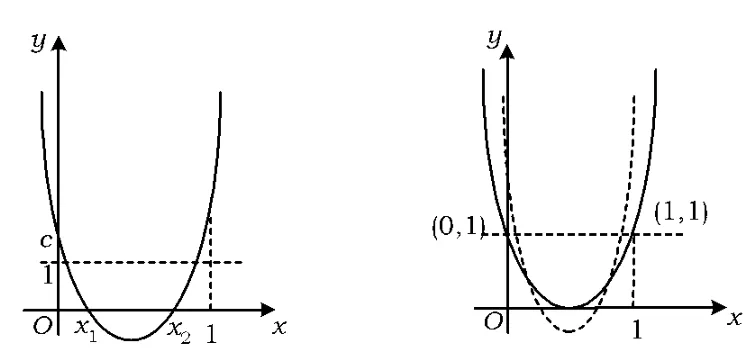
圖4 圖5

解法2 如圖5，由題意設

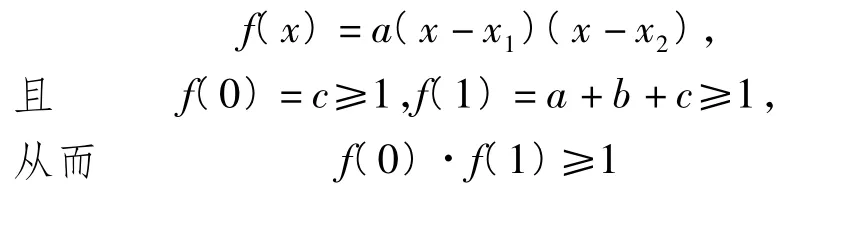
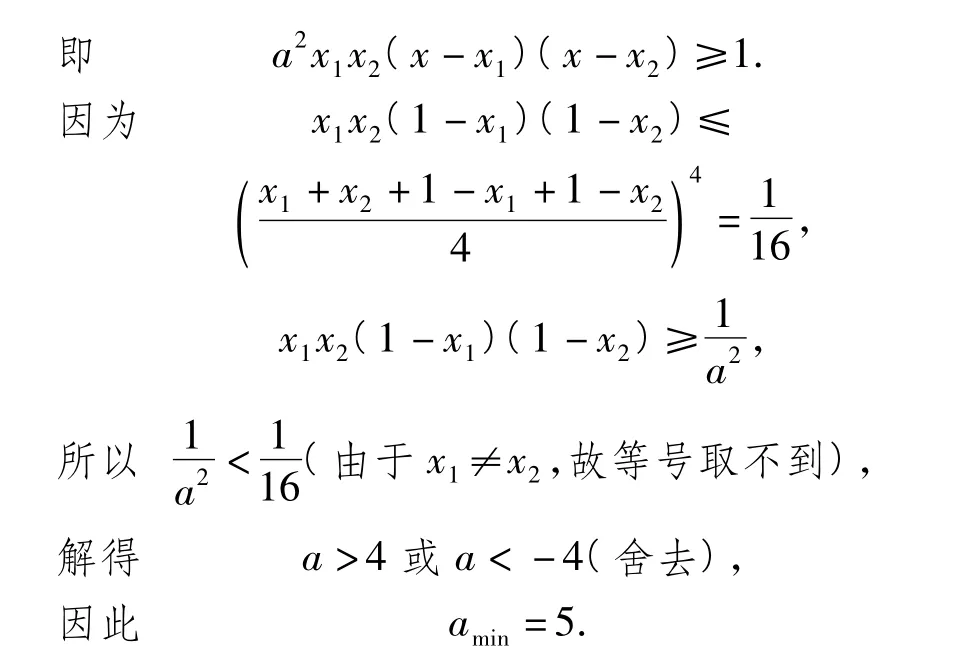
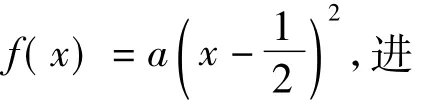
反思 數(shù)學直覺思維的表現(xiàn)形式是以已有的知識、經(jīng)驗和技能為基礎，通過觀察、聯(lián)想、類比、歸納、猜測之后，對研究對象作出較迅速直接的判斷，它不受固定的邏輯約束，能以高度省略、簡化和濃縮的方式洞察數(shù)學關系，能快速解決有關數(shù)學問題.

直覺思維對培養(yǎng)學生的創(chuàng)造力相當重要，而二次函數(shù)又是非常好的訓練背景，平時教師要強調(diào)：直覺思維雖具有創(chuàng)造精神，但由直覺思維得到的猜想需要經(jīng)過邏輯方法加以驗證、猜想或被證明、被推翻.此外，直覺思維能力的形成是一個漸進的過程，不能操之過急.學生的猜想錯誤后，應鼓勵學生重新猜想.總之，只要長期堅持訓練，學生的直覺思維能力就能不斷得到提高，同時學生敏捷的思維和較強的知識綜合運用能力得到逐步培養(yǎng).這不僅有利于智力開發(fā)，更有利于邏輯思維的培養(yǎng)、數(shù)學能力的提高.

［1］ 沈志明.二次函數(shù)的另類最值求法及其引申［J］.中學教研(數(shù)學)，2010(5)：15-16.

［2］ 胡耀宇.抓住圖象就抓住了二次函數(shù)的關鍵［J］.中學數(shù)學教學參考，2006(9)：20-21.

［3］ 唐恒鈞.案例的視角：幾何實驗與幾何證明［J］.中學數(shù)學雜志，2005(4)：16-17.