液面及液面上木塊振動特征的分析

靳偉佳

（華北電力大學電氣與電子工程學院 河北 保定 071003）

漂浮在液體表面的木塊在無阻尼狀態(tài)（只有微振動才能近似滿足）下做簡諧振動的證明是力學及普物教材中常出現(xiàn)的例題或習題［1，2］，在對該問題的討論中，通常均未考慮液體表面的振動以及木塊形狀對木塊振動的影響.本文對柱形容器的液體表面上，柱型木塊、液體表面的振動及圓形、圓錐形木塊在無限大液面上的振動進行了分析討論.

1 理論計算

1.1 柱形容器的液體表面上柱形木塊和液體表面的振動

如圖1所示，一柱形木塊靜浮在圓柱形容器內(nèi)的液體表面，容器的底面積為S0，木塊底面積為S，質(zhì)量為m.平衡時，木塊浸入液體的深度為l，如圖1（a）.使木塊沿豎直方向偏離平衡位置，在無阻尼的情況下，木塊上下振動.取平衡時水面上O點為坐標原點，豎直向上為x軸.設(shè)某時刻木塊位移為x，此時，水面相對于坐標原點亦發(fā)生移動，為簡單計，設(shè)液面始終為平面①這一條件即使對微振動也很難滿足，只是為了分析而引入的假設(shè).，位移為x1，如圖1（b），而木塊相對于水面位移為x2.則x＝x2－x1，木塊運動的動力學方程為

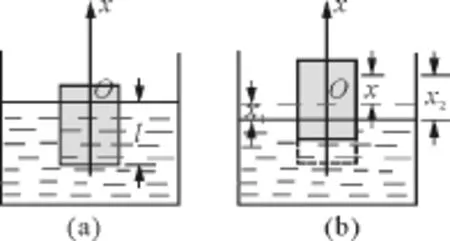
圖1

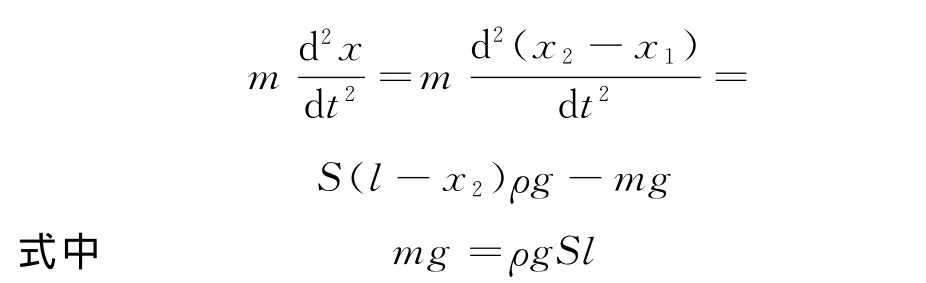
ρ表示液體的密度，代入上式得

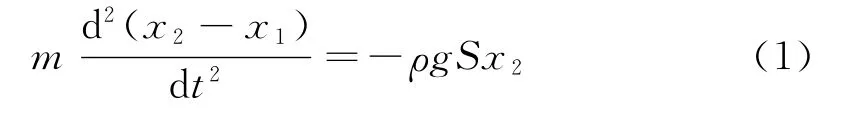
在圖1（b）中，木塊上浮所引起液面下降的體積應(yīng)滿足

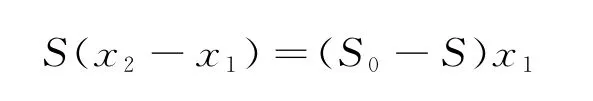
所以

將式（2）代入式（1）得

將式（4）代入式（3）得

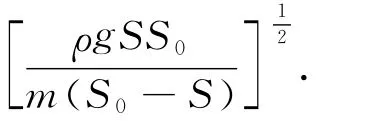
由式（2）所示x1，x2關(guān)系可知，液面亦做與木塊同頻率的簡諧振動，但兩者振動相位相反.

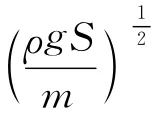
上述討論中，木塊為柱形，木塊的浮力與木塊浸入液體的深度呈線性關(guān)系.若木塊不是柱形，其振動是否仍為簡諧振動？

1.2 球形木塊在無限大液體表面的振動

如圖2所示，一質(zhì)量為m，半徑為R的木球靜浮在無限大液體表面上，其體積的一半恰好浸入液體中 ，如圖2（a），使木球沿豎直方向偏離平衡位置，在無阻尼的情況下，分析木球的上下振動特征.

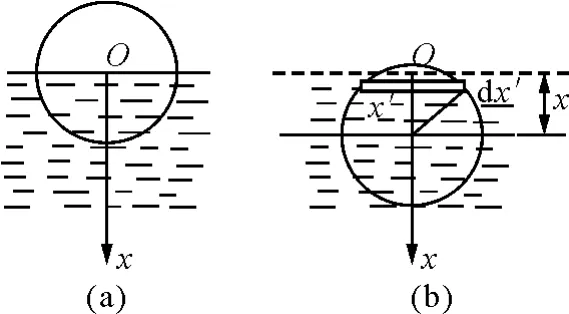
圖2

取平衡時液面上O點為坐標原點，豎直向下為x軸.設(shè)液體的密度為ρ，則球的密度為，當球從平衡位置下移x時 ，如圖2（b），浸入液體中的體積增加了

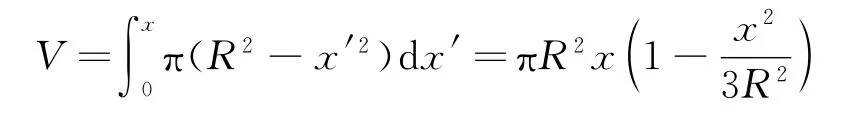
此時木球所受合外力大小

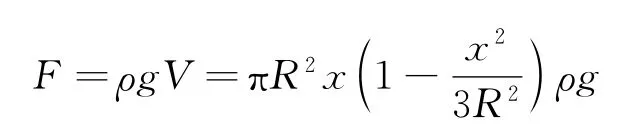
由于木球所受合外力方向與位移方向相反，根據(jù)牛頓第二定律得

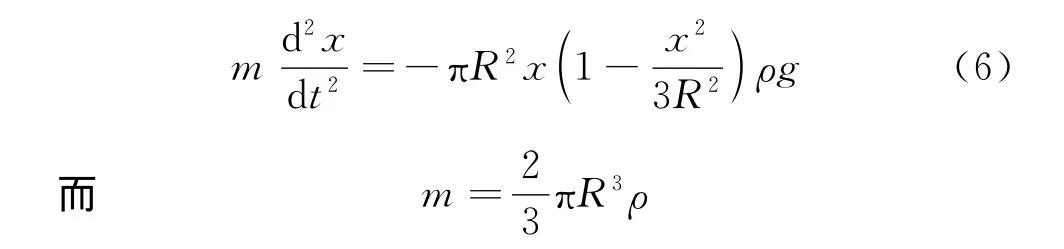
代入式（6）得

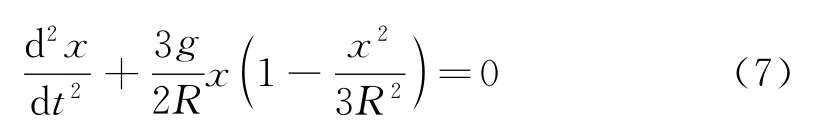
由式（7）可判斷木球的振動不是簡諧振動.

當x＜＜R時，式（7）近似為

即木球做小位移振動時，其振動為簡諧振動.

1.3 錐形木塊在無限大液體表面的振動

如圖3所示，一質(zhì)量為m，高為h的圓錐形木塊在無限大液體表面做無阻尼振動，木塊底面半徑為R，平衡時，木塊浸入液體的深度為l，如圖3（a）.取平衡時水面上O點為坐標原點，豎直向上為x軸.設(shè)某時刻木塊位移為x，如圖3（b），木塊所受合力為

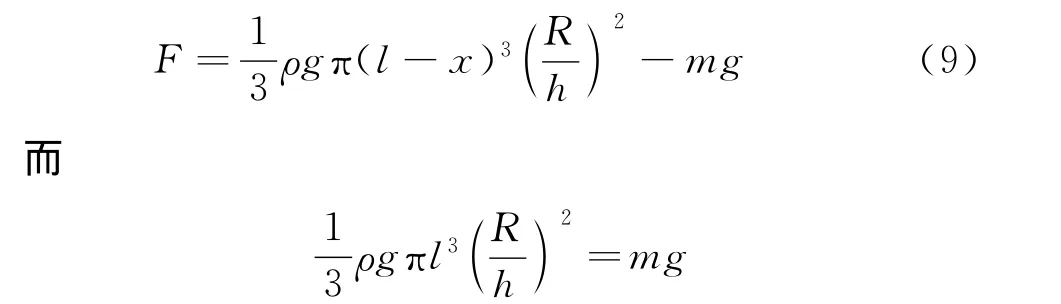
代入式（9）得

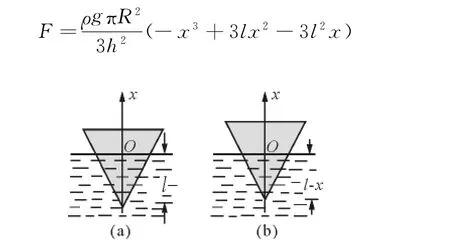
圖3

木塊受到的合外力不存在與位移大小成正比，方向相反的特征，所以圓錐形木塊在液體表面的振動除微振動外不是簡諧振動.

2 結(jié)論

由上述討論可知，由于柱形木塊受到的浮力與木塊浸入液體的深度呈線性關(guān)系，木塊及液體表面都做簡諧振動.對于其他形狀的木塊，由于受到的浮力與木塊浸入液體的深度不再呈線性關(guān)系，木塊不再做簡諧振動.

1 程守珠，江之永.普通物理.北京：人民教育出版社，1982.165

2 趙凱華，羅蔚茵.力學.北京：高等教育出版社，1995.266