基于極值理論的商業銀行同業拆借利率風險度量

李文華

0 引言

利率市場化是金融市場化的關鍵，隨著我國金融市場的逐步開放，利率市場化進程的不斷加快。1996年6月1日我國的利率市場化正式啟動，迄今為止，我國在國債、銀行間市場利率和大額外幣存款利率以及政策性金融債券發行利率上已基本實現市場化。盡管利率市場化為我國商業銀行提供了更加廣闊的營銷價格空間，然而它也導致了商業銀行在經營過程中面臨巨大的利率風險。因此，為規避利率風險，找到適合我國商業銀行現實情況的利率風險度量模型就顯得尤為迫切和重要。

1 理論模型

1.1 VaR方法

VaR(Value at Risk)即風險價值，是20世紀90年代開始在國外盛行的一種金融資產風險評價方法。該方法的主要特征是：在給定的概率水平下(即置信度)，某種證券投資組合或金融資產的價值在未來某個特定時期內的最大可能損失。可用如下公式進行表示：

其中，Prob表示資產價值損失小于可能損失上限的概率；ΔP表示某一金融資產在一定持有期Δt的價值損失額；α表示給定的置信水平；E(W)表示資產組合的預期價值；W表示持有期末資產組合的價值；W*表示在置信區間下最低的資產組合價值。

1.2 極值理論

極值理論，是研究在極端的市場情況下所發生風險損失的一種特殊方法。極值理論主要包括BMM模型和POT模型兩類模型。由于POT模型和BMM模型分別建立在極值理論中的兩個不同的定理基礎之上，加上其獲取極值數據的方法存在巨大差異，共同導致這兩類模型在對極值數據進行擬合的過程中采用不同的分布。其中，BMM模型是一種傳統的極值分析方法，常用于處理季節性數據中的極值問題，而POT模型對數據的數量要求較少，在研究中較為常用的一種新型模型。POT模型有較為嚴格的使用條件：要求超限發生的時間服從泊松分布；要求超限之間彼此相互獨立且服從GPD分布；要求超限與超限發生的時間相互獨立。由于樣本獨立同分布，便可使POT模型的上述前提條件均得到滿足，因此，本文擬采用POT模型進行研究。下文僅僅對POT模型進行簡要介紹：

假設序列{}zt的分布函數為F(x)，Fu(y)為隨機變量Z超過閥值u的條件分布函數，可以將該條件超量分布函數表示為：

由條件概率公式可得：

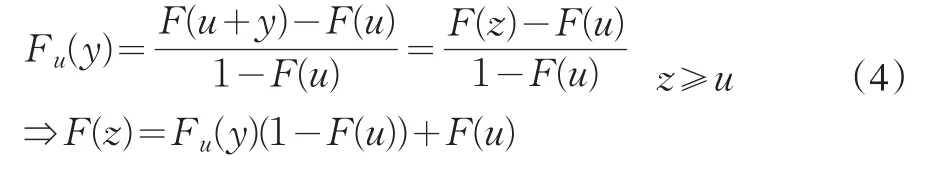
定理1對于一大類分布F（幾乎囊括了所有的常用分布）的條件超量分布函數Fu(y)，存在一個特殊函數使得下式成立：

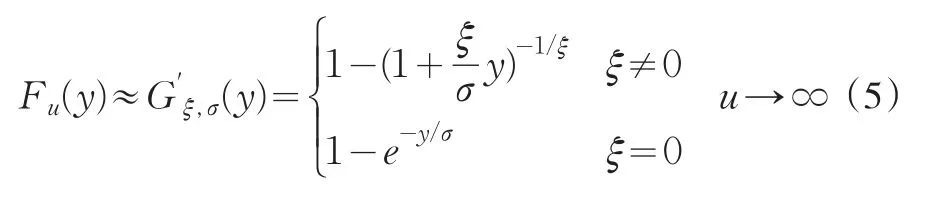
對于給定的某個置信水平 p，可以根據F(z)的分布函數公式得到：

可以看出, 安裝角度增大后, 在渦流發生器安裝位置下游0.6 m 范圍(2.4～3.0 m)尾渦誘導速度增大, 表明尾渦強度增加. 但超過0.6 m后, 18°葉片的尾渦誘導速度反而小于安裝角度12°狀態, ω隨著距安裝位置距離的增加而單調下降, 即強度逐漸減弱, 沒有類似12°情況下2.4～3.0 m間的渦穩定區, 考慮到該區域一般為半模型機頭或機翼前緣, 強渦及渦的快速衰減會影響該區域的均勻性, 因此安裝角12°的效果更好.

2 實證分析

2.1 數據選取與處理

目前，我國銀行間同業拆借市場中融資產品的融資期限通常較短，信用拆借以7日品種為主，7日信用拆借是交易額最大的期限品種，通常能夠占到總交易量的60%左右。鑒于上述原因，本文選取具有代表性的7日品種作為樣本，使用2006年1月4日至2008年12月29日的同業拆借市場七天回購利率為研究樣本，樣本數據總共749個。本文數據均來源于國泰安數據庫。

由于對數回報方式能夠很好地解決數據序列的穩定性問題，因此為了得到穩定的收益率時間序列數據，我們采用拆借利率的對數收益率來進行分析。對數收益率是采用對數一階差分形式，即設第t日的收益率為Rt=lnIBt-lnIBt-1，其中，IBt為第t日銀行間同業拆借市場7日品種的利率。數據分析采用軟件MatlabR2007和Eviews6。對7日拆借利率收益率序列描述性統計結果見表1。

表1 我國銀行間同業拆借利率描述性統計

從表1可以看出收益率序列具有明顯的尖峰厚尾現象。從J－B檢驗結果來看，我們可以在0.01的顯著性水平下拒絕序列的正態性假設。對收益率序列進行單位根ADF檢驗結果來看（見表2），因為檢驗的ADF統計量的值為-17.89，比顯著性水平為10%，5%和1%時對應的臨界值都小，因而拒絕原假設，即序列為平穩序列，不存在單位根。

表2 ADF單位根檢驗結果

接著，本文對收益率序列進行條件異方差檢驗。

首先對我國銀行同業拆借收益率序列做時序圖（如圖1所示），通過圖1可以看出，不同時期波動性的大小也不相同，且序列波動具有明顯的時變性，此外，波動還表現出聚集現象，因而可以判定，銀行間同業拆借利率序列存在條件異方差。

圖1 Chibor7收益率時序圖

圖2 樣本的平均超限函數圖

2.2 模型選取與實證分析

上節對同業拆借收益率序列的正態性、平穩性、自相關性和條件異方差性的檢驗結果表明，銀行間同業拆借收益率序列存在異方差、自相關等特性。

其中，yt表示收益率，?為自回歸系數，εt為新信息，該變量服從一定自由度的t分布。

方差方程形式為：

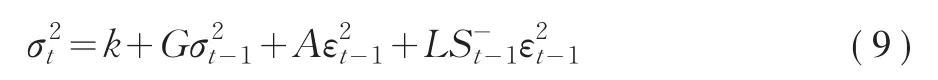
其中，

GJR-t參數估計結果見表3。

表3 Chibor7收益率GJR-t分布擬合參數

接著，本文先將模型擬合的殘差序列進行標準化，并使用GPD模型對殘差序列進行擬合。

根據基于極值理論的POT模型的前提條件的要求，本文使用充分大的閥值u對超限分布進行了GPD擬合。根據圖2，在u＞1處，樣本平均超限函數圖近似直線，具有明顯的Pareto分布特征。

在u允許的情況下，本文認為應選取10%左右的數據作為極值數據組，否則就可能抓不住序列尾部分布的特征，而且，如果樣本內過度擬合，樣本外將不適用。超過數為10%時，u=1.28，超過數為9%時，u=1.44，超過數為11%時，u=1.12，三個閥值均比1大。不失一般性，為此，我們分別在超過數為9%，10%，11%情形下，利用最大似然估計得到各參數以及相應殘差的VaR0.01、VaR0.05、VaR0.10值，接著根據公式(8)、(9)就可以得到相應的同業拆借收益率VaR0.01、VaR0.05、VaR0.10，最終結果如表4所示。

表4 GPD參數估計與同業拆借收益率VaR計算結果

下面對上述計算的結果進行LR檢驗。

通常采用的失敗頻率檢驗法的基本原理是：N為實際樣本天數，M為實際損失大于VaR的天數，將p=M/N稱為失敗率，并且假定計算VaR的顯著水平為α。則可以通過將失敗率p與顯著性水平α進行比較，以此判定模型的準確性：若 p＜α，表明模型的計算結果覆蓋了實際損失，說明模型估計過于保守，高估了風險值；若 p＞α，說明模型低估了風險值。因此，對VaR模型準確性的評估就轉換為，對失敗頻率p與顯著性水平α是否存在顯著差異的檢驗。

對此，Kupiec提出了似然比檢驗，這是一種最佳的檢驗方法[9]。基于零假設條件，統計量LR為：相應地，非拒絕域為滿足條件的M值的區間：

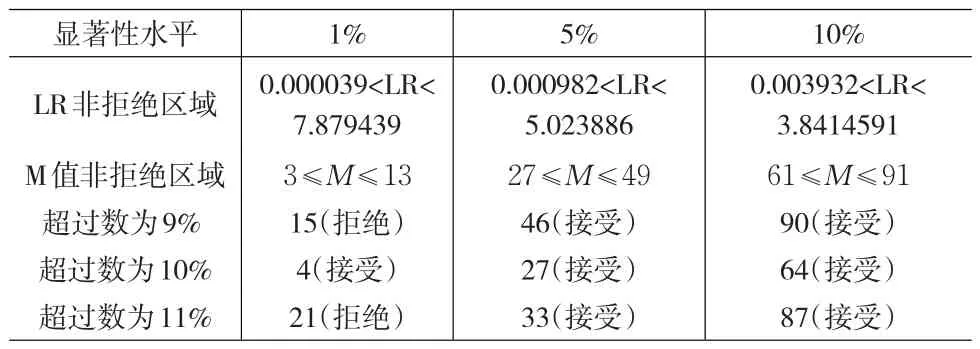
表5 LR檢驗的非拒絕區域及庫柏檢驗結果

根據表5可以看出，經GJR模型過濾計算的日VaR通過檢驗，其對LIBOR收益率風險進行了良好估計。盡管在99%的置信度下，VaR未能很好地度量同業拆借市場的利率風險，失敗率大于1%，這可能是因為VaR只考慮到分布的分位數而并未考慮樣本的整體左極端分布有關。此外，從估計結果可以看出，在95%與90%的置信度下，VaR能夠很好地度量同業拆借市場的利率風險，其失敗率分別小于5%和10%。上述檢驗結果，完全足以說明本文采用模型的合理性和有效性。

3 結論

由于金融數據序列自相關和波動率聚類現象無法滿足極值理論的假設，通常會造成較大估計誤差，因此本文在傳統單純采用極值理論刻畫金融資產收益尾部特征的基礎上，將GJR模型和極值理論有機的結合起來，對商業銀行同業拆借利率風險度量問題進行了深入研究。首先，本文利用GJR模型捕獲同業拆借利率數據中的序列自相關和異方差現象；接著，在獲得近似獨立同分布的殘差序列的基礎上，采用傳統的極值理論對經過GJR模型篩選處理過的殘差進行極值分析，并計算相應的風險價值（VaR），最后；最后，利用LR方法進行回驗測試，對模型的有效性進行進一步檢驗。

從估計結果來看，在95%與90%的置信度下的VaR能很好地度量同業拆借市場的利率風險(失敗率分別小于5%和10%)，這完全足以說明本文采用極值理論與GJR模型相結合的方法對商業銀行同業拆借市場的利率風險進行度量的有效性。在99%的置信度下VaR未能很好地度量同業拆借市場的利率風險，這是由于VaR只考慮到分布的分位數，而沒有對樣本的左極端分布情形進行整體研究。由于CVaR為在一定置信水平下某一資產或資產組合的損失超過VaR的尾部事件的期望值，它能夠比VaR更能全面地對同業拆借收益率的風險值進行度量，而本文只考慮了ARMA-GARCH模型中的GJR模型，沒有對其它的GARCH類模型進行系統分析，因此以后的研究可以嘗試利用其它的GARCH類模型，比如EGARCH模型結合極值理論分析同業拆借收益率的CVaR，以進一步改進度量的精確度。

[1] 李成,馬國校.VaR模型在我國銀行同業拆借市場中的應用研究[J].金融研究,2007,(12).

[2] 鄭堯天,杜子平.基于模型的銀行同業拆借利率風險估計[J].工業技術經濟,2007,(5).

[3] 李志輝,劉勝會.我國商業銀行利率風險的度量研究-以同業拆借市場為例[J].南開經濟研究,2006,(3).

[4] Danielsson,de Vries．Tail Index and Quantile Estimation with Very high Frequency Data[J].Journal of Empirical Finance,1997,(4).

[5] Balkema,de Haan.Residual Lifetime at Great Age[J].Annals of Prob?ability,1974,(2).

[6] Login,F.The Asymptotic Distribution of Extreme Stock Market Returns[J].Journal of Business,1996,(63).

[7] Dumouchel,W.H.Estimating the Stable Index α in Order to Measure Tail Thickness:A Critique[J].Annalyical Statistics,1983,(11).

[8] Embrechets,P.Extreme Value Theory:Potential and Limitations as an Integrared[J].Risk Management Tool,1999,(2).

[9] Kupiec P H.Techniques for Verifying the Accuraniques of Veriyfingt?cy of Risk Measurement Models[J].The Journal of Derivaties,1995,(75).