馬爾可夫鏈在農產品生產價格指數中的應用
諶貽慶,徐 鑫
1 馬爾可夫模型
1.1 概念與基本原理
(1)馬爾可夫鏈定義
給定隨機序列{Xn,n≥0}。如果對任意正整數k≥2,任意的 0≤t1<t2<...<tk+1,任意的非負整數i1,i2,...,ik,E為Xn的狀態空間,條件概率函數總是滿足下式:
P(Xtk+1=ik+1|Xt1=i1,...,Xtk=ik)=P(Xtk+1=ik+1|Xtk=ik)(ik+1∈E)
那么,稱{Xn,n≥0}為離散時間的馬爾可夫鏈,簡稱為馬爾可夫鏈(或馬氏鏈)[2]。
(2)一步轉移概率
稱條件概率 pij(n)=P{Xn+1=j|Xn=i}為馬爾可夫鏈{Xn,n≥0}在時刻n的一步轉移概率,其中i,j∈E,簡稱為轉移概率。設P表示一步轉移概率pij所組成的矩陣,且狀態空間E={1,2,...},則:
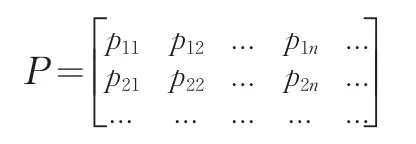
稱為系統的一步轉移概率矩陣。
(3)n步轉移概率
(4)馬爾可夫過程基本原理
按照系統的發展,時間可離散化為n=0,1,2,3,...i,....,對每個系統的狀態可用隨機變量表示,并且對應一定的概率,該概率稱為狀態概率。如果轉移概率只與目前相鄰兩狀態的變化有關,即下階段的狀態只與現在狀態有關而與過去無關,那么這種離散狀態按照離散時間的隨機轉移系統過程,稱為馬爾可夫過程。
馬爾可夫過程具有以下特性:
①設馬爾可夫鏈{Xn,n≥0}的轉移概率矩陣為P=(pij)n×n,如果非負數列{πj}滿足:

則稱{πj,j∈I}為馬爾可夫鏈{Xn,n≥0}的平穩分布。
②設馬爾可夫鏈{Xn,n≥0}有有限狀態空間I={1 ,2,...,n},如果存在正整數n0,使對一切i,j∈I都有,則此馬爾可夫鏈是遍歷的。
1.2 馬氏檢驗
對于隨機序列{Xn,n≥0} ,用 pij表示在(X1,X2,...,Xn)中從狀態i經過一步轉移到狀態 j的頻數,并將(pij)n×n的各列之和除以各行各列的總和所得到的值記為N?j,即:
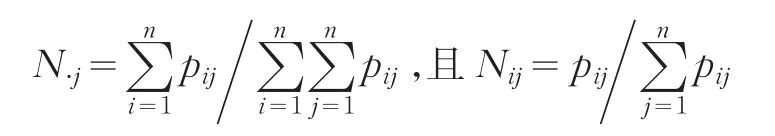
2 運用馬爾可夫鏈預測農產品生產價格指數
2.1 狀態的劃分與轉移概率矩陣
從中國統計年鑒上得知,自農產品生產價格指數創立以來每個季度的數據,取2002~2008年共計28個季度的數據進行研究。具體數據如表1所示。

表1 2002~2008年每季度農產品生產價格指數
將指數分為五個區間,每個區間代表一種狀態,如表2所示。

表2 各區間所表示的狀態
由表1和表2可以統計得到每季度的農產品生產價格指數的狀態轉移次數,所得結果如表3所示。
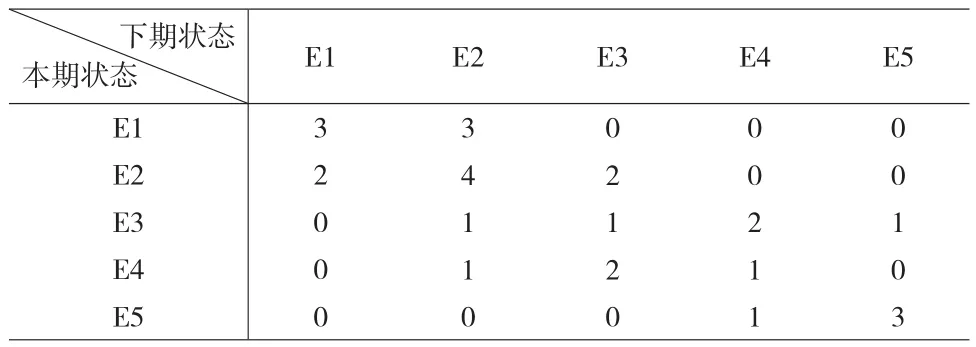
表3 狀態轉移次數
綜上可得,農產品生產價格指數的一步概率矩陣

2.2 對農產品生產價格指數的馬氏檢驗
根據以上所得數據,經計算得到統計量 χ2=36.1582。給定顯著性水平α=0.05,查表可得分位點的值χ2(16)=26.3,χ2>χ2(16),{Xn,n≥0}符合馬氏性,可以利用馬爾可夫鏈來處理農產品生產價格指數。
2.3 農產品生產價格指數馬氏鏈的遍歷性
由以上統計得到的P為一步轉移概率矩陣,可以根據其計算出多步轉移概率矩陣,用P2,P3表示三步轉移概率矩陣。

由以上計算可得,經過足夠的時間,從任一狀態出發,達到任意狀態的概率都大于0,因此各個狀態是互通的,從而可知該馬氏鏈是遍歷的。
2.4 農產品生產價格指數的馬氏鏈穩定概率向量
根據馬氏鏈穩定條件,設π=(x1,x2,...,xn)為原馬氏鏈的平穩分布,從而有下式:

代入數據,得到方程:

解得(x1,x2,x3,x4,x5)=(0.16,0.32,0.2,0.16,0,16)
從而農產品生產價格指數的馬氏鏈穩定概率為(0.16,0.32,0.2,0.16,0,16).由表2可知,初始概率為(0.2143,0.3214,0.1786,0.1429,0.1429)
2.5 對農產品生產價格指數馬氏鏈數據的分析
由于數據的有限性,數據吻合的不是很好,但是數據大體符合實際情況。農產品生產價格指數處于狀態2時最穩定,即當農產品處于100~106時,指數最穩定。一方面,隨著指數的增高,數據將慢慢的趨于不穩定,會很快轉移;另一方面,隨著指數的降低,例如處于100點之下時,數據也是相對不穩定的,會很快轉移。這和實際生活中的現象比較符合。農產品生產價格指數反映了全國農產品生產價格水平和結構變動情況,當指數下降時,間接說明全國主要農產品價格的下跌,在一定程度上就會損害農業生產者的利益,也可能導致農產品市場的供不應求,此時,除了市場機制會起作用外,政府等相關部門也會采取相應的政策,用以支持農業生產,從數據看,2003年第四季度農產品生產價格指數增長較快,而在當時,黨中央作出了一系列積極決策,是政策實施密度較大的一年,這就解釋了上文研究所得的結果。
當農產品生產價格指數持續升高時,說明農產品價格整體在高位運行,農產品市場可能會出現供過于求的狀況,比如2007年和2008年,農產品價格持續上漲,針對這一情況,中國國務院在2008年1月30日晚發布了《中共中央國務院關于切實加強農業基礎建設進一步促進農業發展農民增收的若干意見》。《意見》稱,切實保障農產品供給與穩定市場價格是中國政府當前和近期工作的主要任務。從此可以看出,當農產品價格指數偏高時,也就是農產品價格升高時,除了市場機制外,更多的是中央等部門在發揮市場調節的作用。
2.6 對2009年農產品生產價格指數的預測
2008年第四季度的農產品生產價格指數為101.61,處于狀態2,即此時的初始概率為π(0)=(0,1,0,0,0),所以2009年第一季度與第二季度的指數狀態概率向量為:


和實際數據相比(實際中,2009年第一季度農產品生產價格指數為94.14,第二季度為93.39),這有一定的出入,預測顯示,最穩定的區間仍然是區間2,即處于100-106之間,但指數值處于第一區間的概率明顯上升,而處于高水平的區間的概率很小(幾乎為0),說明農產品價格在2009年將有可能遭遇一輪下跌的趨勢,而在現實情況下,2008年爆發的金融危機對我過的農業影響不容忽視,2009年中央也出臺了一系列針對金融危機的農業新政策。為了剔除金融危機的影響,以2009年第一季度為初始數據,則此時的初始向量為π(0)=(1,0,0,0,0),則第二季度的概率向量為:
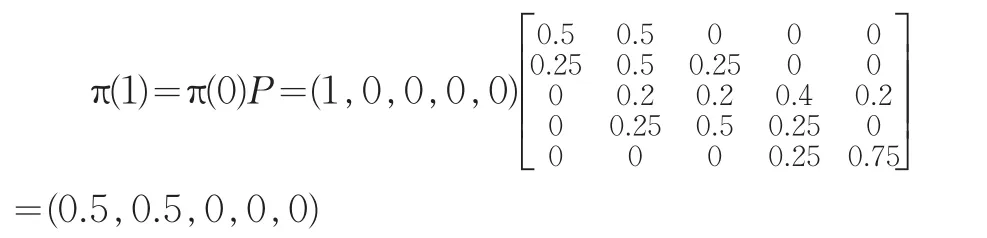
這說明,如果農產品生產價格指數持續在低位運行,那么其持續在低位運行的概率將大大增加,僅僅依靠市場機制的作用,很難發揮其維穩的作用,從而更加的需要中央等有關部門干預農產品市場。
3 農產品生產價格指數未來走勢的預測
3.1 指數走勢的轉移概率矩陣
整理表1,再加上國家統計局最新發布的2009年前三季度的數據(分別為94.14,93.39,97.33),觀察數據,取±2個點的值為分界線,增長超過一點視為上升,下降超過一點視為下跌,在一點之內視為持平,分別記做狀態E1,E2,E3。根據統計農產品生產價格指數的統計規律,統計伊始的第一季度視為持平從而有表4。

表4 2002~2009年三季度供31個季度指數的走勢
根據可以計算出指數的狀態轉移情況,如表5。

表5 農產品生產價格指數的狀態轉移情況
得到狀態轉移概率矩陣P:

3.2 馬氏檢驗
根據以上所得數據,經計算得到統計量 χ2=20.2994。給定顯著性水平α=0.05,查表可得分位點的值χ2(4)=9.49,χ2>χ2(4),{Xn,n≥0}符合馬氏性,可以利用馬爾可夫鏈來處理。
3.3 指數走勢穩定概率向量
設指數狀態向量為(x1,x2,x3),其中x1代表上升,x2代表持平,x3代表下跌。再將各項數據代入上述穩定條件方程:

所以關于農產品生產價格指數走勢的穩定概率向量為(0.3576,0.3329,0.3059)
3.4 對產品生產價格指數走勢的穩定概率向量的分析
通過以上的分析,隨著以后每個季度對農產品生產價格指數的統計,指數將以35.76%的概率上升超過兩點,以33.29%的概率維持在兩點之內,以30.59%的概率下跌超過兩點。所以可以看出,農產品生產價格指數在長期內,上升的概率將大于下跌的概率,從而在長期內,國內主要農產品的價格將更有可能呈現出普漲的局面。
[1] 何迎暉,錢偉民.隨機過程簡明教程[M].上海:同濟大學出版社,2004.
[2] 彭志行,夏樂天.馬爾可夫鏈及其在股市分析中的應用[J].應用數學,2004,(17).
[3] 夏莉,黃正洪.馬爾可夫鏈在股票價格預測中的應用[J].商業研究,2003,(10).

