光電吊艙無角位移被動減振系統研究
李玉龍,何忠波,白鴻柏,郝慧榮,李冬偉
(軍械工程學院,石家莊 050003)
光電吊艙無角位移被動減振系統研究
李玉龍,何忠波,白鴻柏,郝慧榮,李冬偉
(軍械工程學院,石家莊 050003)
根據某型光電吊艙無角位移減振的需求,利用分級減振的設想,設計了一組內外框架減振器,計算了減振器剛度、阻尼系數范圍,并對減振器進行了合理的布局,建立了減振系統的Solidworks三維模型,在ADAMS中進行了振動仿真分析,得出單方向輸入時系統的幅頻響應曲線,并對系統參數進行了優化,確定了減振器的剛度、阻尼系數的最優值,結果表明,該系統實現了三向相等剛度,解除了系統三個方向的線振動耦合,保證了荷載基準與底座基準振動狀態下無相對角位移。
被動減振;無角位移;減振器;光電吊艙
現代戰爭中占據空中偵察、作戰的優勢越來越重要,作為偵察、監測、校射及打擊效能實現的重要裝備,機載光電偵察設備日益受到重視,各國競相研制。但是,由于機載光電偵察設備處在飛機高頻振動、姿態變化、風阻力矩及起降時沖擊等一系列復雜振動環境下,確保光電偵察設備的穩定,使其具有良好的成像質量成為亟待解決的難題。因此,對光電偵察設備采取減振措施非常必要[1-2]。
目前工程上常采用主動隔振和被動隔振組合的方式對振動進行隔離。被動隔振主要對中高頻振動隔振(高于20 Hz);主動隔振主要是對低頻振動(一般低于20 Hz)采用陀螺儀實時感知并修正,由于受到陀螺帶寬、電機的運轉特性以及機械結構固有頻率等因素限制,目前控制帶寬低于25 Hz,所以,20~500 Hz及以上的振動擾動需采用被動隔振方式[3]。根據現有的光電吊艙多框架減振結構,本文設計了一組內外框架減振器,并用Solidworks建立了內外框架減振器及簡化吊艙的三維模型,計算了各減振器的參數范圍,又通過Adams/Vibration仿真分析了減振器安裝于系統后的減振效果,優化了減振器阻尼系數。結果表明,該內外框架減振器組合而成的減振系統不僅可以達到對中高頻(20~500 Hz)被動隔振的目的,又可以消除不同方向線振動耦合引起的角振動,實現三軸向的振動解耦,滿足底座與荷載間無角位移的減振要求。
1 減振器結構及減振系統設計
設計減振器的目的是通過減振器組成的被動式減振系統隔離荷載外部的高頻振動,并解除不同坐標方向之間的線振動耦合。某型光電吊艙減振器的設計要求為:減振器滿足高精度小型化的前提,且在5 g(20~500 Hz)振動時,無角位移減振器三向減振效率不小于20 dB,最大角位移優于(40 μrad)8"(曝光時間內)。
1.1 減振系統設計及模型
根據以上要求,采取分級衰減的思想設計兩層減振器,內、外框架減振器截面圖如圖1(a)、(b)所示:外框架減振器圖1(a)內部軸與外殼之間是圓柱副接觸,軸的凸肩通過壓縮上下兩塊金屬橡膠元件實現軸向的減振;內框架減振器圖1(b)軸與組合體實現圓柱副約束,組合體與外殼之間是平面副約束,以實現垂直于軸的兩個轉動副的約束,且該軸在外殼體的直線導向槽內,以限制垂直于導向槽方向的平動;三組金屬橡膠件實現平動自由度上的線振動衰減。減振系統在結構布局上主要采用分級減振和單級減振器在某平面內對稱組合的方式,既限制繞X,Y,Z三軸的轉動自由度,又在內外兩層減振器上實現沿X,Y,Z三軸向的平動減振,減振系統結構如圖1(c)所示:四個外框架減振器和飛機平臺連接,通過外框架減振器的對稱布置限制繞Y軸的轉動,并實現沿Y軸方向的減振;八個內框架減振器的對稱布置限制繞X,Z軸的轉動與Y向的平動,并實現X,Z軸兩向的減振,整個系統組合后實現了荷載與底座間三向無角位移減振。圖1(c)中,荷載內部安裝光電偵查攝像設備;底座等效為吊艙固連與飛機的平臺;荷載基座與外框架固連[4-6]。
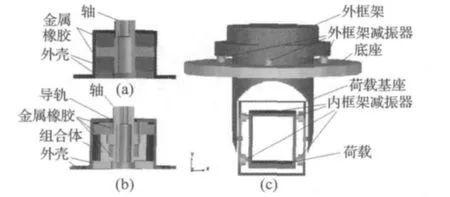
圖1 減振器及系統結構圖Fig.1 Schematic diagram of dampers and photoelectric pod
由以上隔振系統結構分析可知,本文設計的光電吊艙隔振系統從機械結構上限制了繞X、Y、Z三軸的轉動,與傳統的三向(或多向)剛度減振器相比,本文設計的減振器為單向剛度減振器的組合,采用分級減振的方法實現光電平臺的振動衰減,即從結構上實現了系統僅能沿X,Y,Z三方向平動。因此,該系統每單個方向為單自由度系統,可簡化為如圖2所示的形式。
由牛頓第二定律可導出單方向運動微分方程:Mx··+cx·+kx=cy·+ky(1)
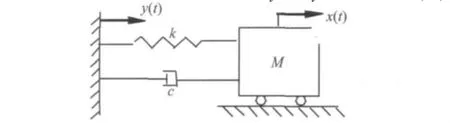
圖2 減振系統單方向減振簡圖Fig.2 Diagram of isolation in one direction
若令光電吊艙內荷載質心沿X,Y,Z軸的位移分別為 x,y,z;底座沿 X,Y,Z 軸的位移分別為 u,v,w;沿 X,Y,Z軸隔振支撐對象的質量分別為mx,my,mz;單個外框架減振器剛度阻尼分別為:kd1,cd1;單個內框架減振器軸向(側向與軸向相同)剛度和阻尼分別為:kd2,cd2。
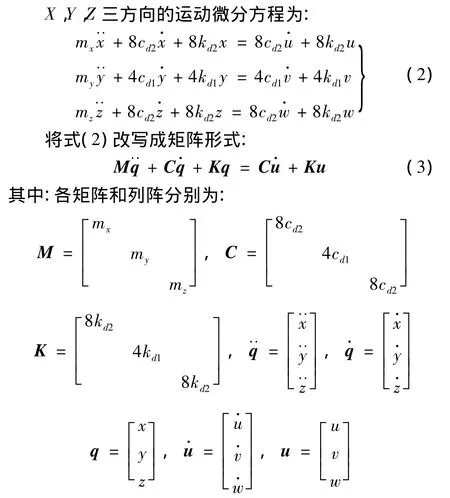
可見,該系統的質量矩陣M、剛度矩陣K和阻尼矩陣C均為對角矩陣,即系統X,Y,Z三方向振動相互獨立,無耦合。
1.2 減振系統設計理論基礎
減振系統設計重點在于確定減振器的剛度系數和阻尼系數,使系統達到比較滿意的響應。由于系統單個方向可簡化為單自由度系統,設單方向外部干擾振動頻率為ω,物體的質量為m,減振器的剛度系數為k,減振器的阻尼為c,系統的阻尼比為ζ,固有頻率為ωn。則隔振系統位移傳遞率為:
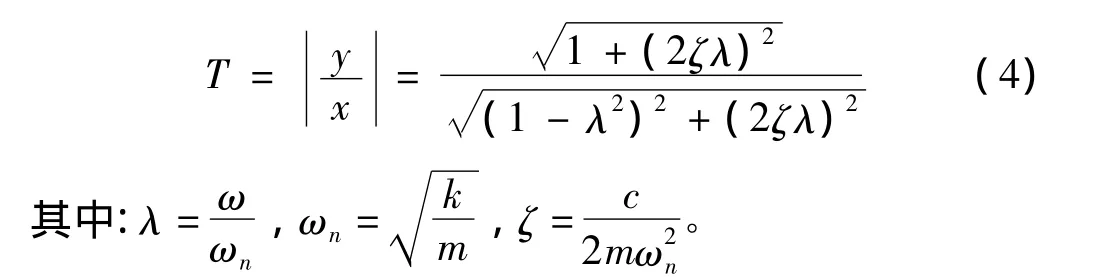
T,λ和ζ相互關系曲線如圖3所示。
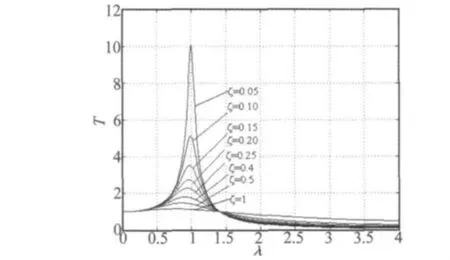
圖3 T,λ和 ζ的關系Fig.3 Relation curves of T,λ and ζ
1.3 減振器參數計算
實際中常根據負載重量來平均分配每個減振器的公稱載荷,再根據具體的參數和結構空間選取或定制減振器結構尺寸[3]。由減振器的布置方式知,外框架減振器和內框架減振器均為并聯,則剛度分配公式為:

其中:kd,cd分別為單個減振器的剛度和阻尼;kz,cz分別為在對應方向上總體減振需要的剛度和阻尼;n為減振器個數。
若設內框架總質量為m1=10 kg,外框架總質量為m2=20 kg(包含減振器質量)。由于指標要求在5 g(20~500 Hz)振動時,三向減振效率不小于20 dB,即20lgT≤-20,則有T≤0.1。又由于:

ω取需要衰減的最小頻率 f=20 Hz(ω=2πf=125.6 rad/s)計算,有4.4 Hz<fn<6.1 Hz(固有圓頻率:28 rad/s≤ωn≤38 rad/s)。
對于外框架減振系統,系統在Y軸方向的總剛度由式(8)計算:15 680 N/m≤kz1≤28 880 N/m;由式(5)可計算單個外框架減振器軸向剛度:3 920 N/m≤kd1≤7 220 N/m。
對于內框架減振系統,系統在X軸與Z軸方向的總剛度由式(8)計算:7 840 N/m≤kz2≤14 440 N/m;由式(5)可計算單個外框架減振器軸向剛度:980 N/m≤kd2≤1 805 N/m。
2 仿真結果與分析
在Solidworks中建立減振系統模型并導入ADAMS中,根據實際情況,創建個零件之間的相互約束關系,并假設各零件為剛體,金屬橡膠為無質量的線性彈簧,內框架(帶荷載)質量m1=10 kg,外框架質量為m2=8 kg,內框架減振器質量m內=0.16×8=1.28 kg,外框架減振器的質量m外=0.18×4=0.72 kg,定義材料質量時設定密度以確保質量恒定,且各零件的轉動慣量采用設定材料相應密度后軟件自動計算值[7]。另外,由于降低減振器剛度系數時,減振器變形量會增加,變形量過大會造成減振器質量過大,增大系統尺寸。因此,根據1.3節計算,可選單個外框架減振器剛度為:kd1=7 000 N/m,單個內框架減振器兩向剛度為:kd2=1 800 N/m。若暫取阻尼比ξ=0.1,則c=0.2,即有:cd1≈37 N/(m/s),cd2≈10 N/(m/s)。
系統沿X,Y,Z方向的固有頻率如表1所示。

表1 沿X軸、Y軸和Z軸三方向的固有頻率Tab.1 Nature frequency of three-axis and damping ratio
2.1 頻域響應仿真分析
在底座中心位置處的X軸、Y軸及Z軸方向建立三個輸入通道及激振器,三個激振器可使模型產生三個方向相互垂直的指定頻率范圍內的正弦作用力,模擬底座的振動;并在底座中心、外框架中心及荷載中心位置分別建立輸出通道沿三個方向的位移、加速度的輸出通道,檢測系統各零件在不同振動狀態下的響應情況[7]。
設定各部件均處于平衡位置,用ADAMS/vibration模塊對該減振系統在不同頻率下的減振效果進行仿真,分別給出沿三個輸入通道以1~500 Hz的正弦掃頻作用力,荷載加速度響應的幅頻特性曲線及底座加速度響應的幅頻特性曲線如圖4所示,其中,6 Hz-hezai-X(Y、Z)為隔振系統荷載X(或Y、Z)方向的加速度響應曲線,6 Hz-dizuo-X(Y、Z)為底座 X(或 Y、Z)方向的加速度響應曲線。
分析圖4中的各曲線,以底座的響應為參考(輸入激勵),評估荷載的振動情況:三向響應曲線均在外部干擾為6 Hz(固有頻率)附近時荷載的振動響應最大,當干擾大于8.2 Hz時起減振作用,在20 Hz時光電吊艙荷載的加速度響應約為輸入的1/10(衰減約20 dB),100 Hz以上時甚至可以達到0.1%(衰減約40 dB),達到了在20 Hz以上振動時三向衰減不小于20 dB的指標要求。

2.2 單輸入時三方向的傳遞函數
由以上仿真結果還可以得到沿單方向輸入時三方向的輸出位移的傳遞函數如圖5所示。
其中,6 Hz-hezai-X(Y,Z)為隔振系統荷載 X(或 Y,Z)方向的位移響應曲線,6 Hz-dizuo-X(Y,Z)為底座 X(或Y,Z)方向的位移響應曲線。由5圖可知,激勵沿X(或Y,Z)單方向輸入時,荷載僅在X(或Y,Z)但方向上有位移響應,另外兩方向均位移響應近似為零,且僅在6 Hz附近有唯一峰值。可見,該隔振系統X,Y,Z三方向的振動互不干涉,無相互耦合。仿真結果證明,該內外框架減振器組合后能夠實現三軸向的振動解耦,底座與荷載間無相對角位移,且能實現三軸向線振動的衰減。
3 減振系統參數優化
由于提高系統的隔振率不但要保證系統有一定固有頻率,還要控制阻尼比使系統在固有頻率附近影響不至于過大,為了進一步提高系統的減振效果,需對系統參數進行優化。以X方向為例對減振器阻尼進行優化,結果如圖6所示,橫軸為內框架減振器在X方向的阻尼系數,縱軸為荷載在固有頻率處的加速度響應幅值。
當X方向單個減振器阻尼系數分別取1 N·m/s,3 N·m/s,5 N · m/s,10 N · m/s,15 N · m/s,20 N·m/s,25 N·m/s,30 N·m/s時,荷載 X 向加速度響應的幅頻特性如圖7所示。
由圖7可得,當單個內框架減振器X方向阻尼系數為10 N·m/s時,系統在固有頻率附近響應相對較小,且在高頻振動時有較好的減振效果。按照同樣的方法對Y,Z方向減振阻尼系數進行優化,結果表明單個外框架減振器Y方向阻尼系數應取40 N·m/s,單個內框架減振器Z方向阻尼系數應取10 N·m/s,優化后系統的三向固有頻率和阻尼比如表2所示。
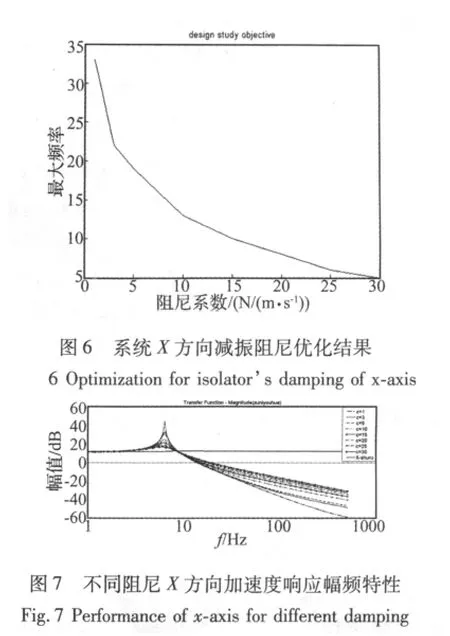

表2 優化后系統三向固有頻率和阻尼比Tab.2 Optimize result of nature frequency and damping ratio
由以上分析可知,如果繼續降低固有頻率(即減振器剛度系數),減振效率會繼續加大,但是考慮到減振器的變形量會增加[8],減振器的尺寸也相應的增大,無法在小巧的光電吊艙中使用,仿真結果證明本文選取的減振器剛度系數為最優值。
4 結論
本文根據某光電吊艙無角位移減振的需求,利用分級減振的設想,設計了一組內外框架減振器,計算了減振器剛度、阻尼系數范圍,并對減振器進行了合理的布局,建立了減振系統的三維模型,并在ADAMS中進行了振動仿真分析,得出了單方向輸入時系統的幅頻響應曲線,荷載位移在各方向的傳遞函數曲線。結果表明,該減振系統滿足設計要求,實現了三相等剛度及三個方向的振動解耦,保證了荷載基準與底座基準角位移的一致性。還通過仿真試驗對系統參數進行了優化,確定了減振器的剛度系數和阻尼系數最優值,為下一步實物試驗打下了基礎。
但是,從工程化的角度來說,由于存在加工裝配誤差,各減振器的一致性和絕對對稱布置均很難保證,各零件也并不是剛體,且金屬橡膠是一非線性結構阻尼材料并不是線性無質量彈簧,而仿真試驗中都做了理想簡化,因此,仿真與實際還有一定的差距,需要在下一步工作中進行詳細的設計、工程實現與試驗驗證。使減振器結構更加緊密,加工更加簡便,一致性更好,最終實現該減振系統的工程應用。
[1]張 葆,賈 平,黃 猛,等.動載體成像系統底座無角位移減振器的設計[J].光學技術,2003,29(4):464 -466,472.
[2]張 葆,賈 平,黃 猛.動載體成像模糊的振動被動控制技術[J].2003,29(3):281 -283.
[3]朱石堅,樓京俊,何其偉等.振動理論與隔振技術[M].北京:國防工業出版社,2008.
[4]甘至宏.光電吊艙內框架減振系統設計[J].光學精密工程,2010,18(9):2036 -2043.
[5]田素林,白鴻柏,張 葆,等.機載多框架光電吊艙無轉角隔振方式設計[J].長春理工大學學報,2009,32(4):538-541.
[6]馬芳賢,王會利,牟讓科.航空用新型金屬橡膠減振器設計分析研究[J]. 振動工程學報,2008,21(S):106-110.
[7]陳立平,張云清,任衛群,等.機械系統動力學分析及ADAMS應用教程[M].北京:清華大學出版社,2005.
[8]王 珂,顧逸東.空間科學實驗柜被動式減振系統研究[J]. 空間科學學報,2006,26(6):470-476.
Non-angular displacement passive vibration isolation system for optical pod
LI Yu-long,HE Zhong-bo,BAI Hong-bai,HAO Hui-rong,LI Dong-wei
(Ordnance Engineering College,Shijiazhuang 050003,China)
According to the demand of non-angular isolation for a certain optical pod,a new type of inner and outer shock absorbers which can limit the angular displacement between the base and load were designed.The stiffness and damping of the absorbers were calculated,and the vibration isolation system on which the two absorbers are reasonably placed was also designed.The three-dimensional models of the absorbers and the system were built by using the software of Solidworks,then the system was simulated by using ADAMS/vibration.The frequency response curves were obtained,and the optimal stiffness and damping were also achieved by the simulation optimization,The results show that the new system has all the same stiffness in three directions,and can remove the linear vibration coupling and the relative angular displacement between the load and base.
passive vibration isolation;non-angular displacement;shock absorber;optical pod
TH113.25
A
國家自然科學基金(50775220);軍械工程學院原始創新基金(YSCX004);武器裝備“十一五”預先研究資助項目(51312040405)
2011-06-20 修改稿收到日期:2011-08-29
李玉龍 男,碩士生,1986年生

