基于Preisach理論的形狀記憶合金溫度－位移遲滯仿真研究

劉旺中，陳照波，侯守武，沈那偉，焦映厚

(哈爾濱工業大學 機電工程學院，哈爾濱 150001)

基于Preisach理論的形狀記憶合金溫度－位移遲滯仿真研究

劉旺中，陳照波，侯守武，沈那偉，焦映厚

(哈爾濱工業大學 機電工程學院，哈爾濱 150001)

智能材料如形狀記憶合金(Shape Memory Alloy，SMA)已經廣泛應用于驅動器和傳感器的設計，實現定位和主動控制目的。然而，受遲滯影響，SMA驅動器的工作精度大大降低，限制了其應用。多數智能材料中，選擇Preisach理論成為遲滯建模工具，近年來，也涉及到SMA材料系統。討論運用Preisach模型描述SMA驅動器系統的遲滯行為，尤其針對驅動器系統的模型建立過程，修正經典Preisach模型的幾何解釋和數值實現方法。最后，引入Gobert給出的Preisach平面的辨識函數執行仿真計算，數值結果表明該模型能夠很好地描述SMA驅動器的遲滯行為。

形狀記憶合金;Preisach理論;遲滯;驅動器;參數辨識;Matlab程序;數值試驗

遲滯現象常見于許多科學領域，如物理材料中的磁性材料，壓電陶瓷和形狀記憶合金等［1－2］。遲滯系統為典型的非線性系統，實際應用中，由智能材料形成的驅動系統，需要消除這類非線性，它的存在不僅降低系統的控制精度，還會產生與輸入信號幅度相關的相位移和諧波失真，從而削弱閉環系統中的反饋作用，甚至造成系統的不穩定，因此完成遲滯非線性的建模十分重要［3］。

如圖1所示，一個簡單的遲滯結構可表示為簡單的遲滯系統轉換器X(t)、系統的輸入信號u(t)及轉換器的狀態即輸出信號x(t)的組合形式，假設遲滯函數是瞬時的，附加的動力學在x(t)和u(t)之間單獨建立［4］。本文u(t)視為SMA絲驅動器的溫度，溫度的變化引起SMA材料的晶格相變，加熱和冷卻兩個階段，材料參數和狀態變化不發生重疊，即具有遲滯效應，類似于圖2中的曲線變化軌跡。這類遲滯轉換器的輸入－輸出關系具有多分支非線性特性，分支結構的轉換點發生在輸入極值點處，遲滯狀態的變化不僅受制于系統的輸入－輸出的瞬態值，而且還與系統輸入的歷史值有關［5］。

圖1 遲滯系統的組成圖Fig.1 Schematic representation of hysteretic systems

見圖2，遲滯系統的特征表現為相同的輸入可能會得到不同的輸出，同樣，相同輸出也可由不同輸入決定，輸入－輸出表現為多映射關系。O點為初始時刻的輸入點值，對應輸出為0，假設第一次輸入到達t1時刻的A點，滿足實際驅動器的輸出飽和值，曲線OA形成系統的邊界區域，稱作遲滯曲線的主環;終點tn時刻的B點處于次環位置，同樣輸入u(tn)映射了系統的多值輸出［6］。

圖2 多個－分支非線性的遲滯例子，遲滯分支也被稱為轉換曲線Fig.2 An example of hysteresis multi－branching nonlinearity.Hysteresis branches are also called transition curves

依據描述遲滯效應不同的角度，系統模型可粗略劃分為基于物理機理和唯象型，前者典型例子如廣泛用于鐵磁材料的Jiles－Atherton模型［7］，認為遲滯源于材料缺陷位置疇壁之間的相互牽制作用;后者如用于磁性材料遲滯描述的Preisach理論，模型具有較強的數學泛化能力，經典Preisach模型常用于描述率無關遲滯行為［8］;修正經典模型，考慮動力學行為的影響，描述更高階遲滯，如 Moving Preisach 模型［9］、Generalized Preisach 廣義模型［10］和動力學遲滯模型［11］。鑒于 Preisach理論的廣泛應用和所表現出來的局部記憶性和次環全等性兩個重要特性，探討用于SMA絲驅動器的遲滯建模的原理和實現過程，為后續嵌入SMA絲驅動的應用系統分析和設計打下基礎。

1 遲滯轉換器的數學模型

1.1 Preisach模型

Preisach理論中，最基本的假設是將系統看作一組連續雙穩態遲滯單元γαβ的權重并聯總和，如圖3所示。給定隨時間變化的輸入，影響所有遲滯單元的輸出狀態，輸出值和μ(α，β)乘積之和提供系統的輸出，μ(α，β)為 γαβ的權重系數［12］。

式中：權重函數μ(α，β)定義為Preisach分布函數，形成的函數集合 μ(αi，βi)描述了遲滯單元(αi，βi)對系統輸出的貢獻量。

為所有基本遲滯單元施加相同輸入值u(t)，單元輸出與權重函數μ(α，β)乘積，即等價于區域內的雙重積分得到系統輸出。

1.2 Preisach模型的幾何說明

圖4中的平面S上每一點(αi，βi)有一特別的基本遲滯算子 γαiβi，表明遲滯單元 γαβ與(α，β)點之間的一一對應關系。平面 S稱為Preisach平面，γαβ記為Preisach單元，多數研究將遲滯單元表示成輸入－輸出的矩形環形式，雙穩態參數分別記為數值量“+1”和“－1”，S 平面外，γαβ值均為“0”，則單元的輸出狀態也為零;輸出狀態量由系統輸入控制，單元符號α和β表示輸入值的“上”和“下”。變化的輸入極值點形成的折線L(t)將三角區域平面S劃分成S+和S－，分別包含不同狀態的離散遲滯單元點及對應的權重函數值;這個三角圖形S平面的頂點坐標，表示輸入u(t)的最大值。

2 SMA絲驅動器的溫度－位移遲滯

2.1 模型建立

考慮SMA絲驅動器中的遲滯曲線的形成，為簡單起見，將SMA驅動器所需驅動源的溫度量作為系統輸入u(t)，x(t)為輸出位移，當溫度值為零時，系統輸出也為零;值得注意的是，SMA實際溫度值不為零，表現為自然環境的溫度值T∞，溫度值為零的狀態標記無外界能量輸入的起始點。如圖5(a)，隨著輸入單調增加到α1值，激活部分遲滯算子，開關值α小于α1的單元輸出狀態顯示為“+1”;幾何意義上，形成狀態不同的區域集合，將三角平面S劃分成兩個區域：S+由點(α，β)構成，對應單元輸出值為+1和區域S－，遲滯單元由狀態輸出值“－1”的集合構成。兩區域之間的界面為α=u(t)+β直線，由圖4中的符號L(t)表示，運動方向朝上，直至α1到達最大值時，運動停止。

如圖5(b)，輸入值從α1單調下降到某個值β1，所有在集合S+(t)帶有β開關值大于β1的遲滯算子轉換為“－1”值，進入S+區域，S+和S－兩個區域之間由兩個分界線連接。隨著溫度從α1到β1單調減少，形成界面處的斜線形式為β=u(t)－α。當輸入達到β1的最小值，斜線運動終止;圖5(c)，記錄下一步的兩組輸入變化值。由圖5給出的Preisach理論的幾何解釋表明Preisach平面上陰影和空白部分面積所構成的集合值反映了系統輸入信息變化。

圖5 基于Preisach理論的SMA遲滯的幾何表示Fig.5 Geometrical interpretation of the SMA hysteresis based on Preisach theory

從上述分析可知，對應增加和減少輸入兩類情形，得到以下結論：任意瞬時，三角區域S被分割成兩組：S+(t)和S－(t)，分別包含不同狀態值“+1”和“－1”的遲滯算子單元;連接S+(t)和S－(t)區域的是一條規則階梯線，記錄不同的α和β坐標，坐標點值包含著歷史輸入中的局部最大值和最小值的瞬時信息。

因此，任意瞬時，利用區域S+和S－的定義，輸出方程(1)的積分式可寫成：

其中：任意(α，β)∈S－(t)，γαβ［u(t)］= －1 和對于任意(α，β)∈S+(t)，γαβ［u(t)］=+1，S=S++S－。

式(2)表明Preisach模型的輸出大小與三角區域S的劃分動態相關，函數L(t)定義了實時更新的界面信息，記錄歷史輸入的極限值［13］。

2.2 數值實現

經典的Preisach模型直接用于SMA絲驅動器遲滯的表達，會遇到很多困難。首先，估計式(1)和式(2)中的雙重積分;其次，決定Preisach平面的遲滯算子γαβ數量和獲得相應的Preisach分布函數μ(α，β)等;這些問題導致模型的執行程序和處理過程不但消耗計算資源，不符合實時控制要求，且帶來較大的累積誤差，其中，權系數的辨識函數的要求也更加苛刻。文獻［14］表明，直接處理經典的Preisach理論模型的數學公式，以參數辨識方法找到等價函數形式，可有效解決上述問題，且由于減少求導獲取權函數的環節，不僅可以減少數值計算誤差，且簡化了Preisach模型的處理。

按照文獻［15］的遲滯模型辨識方法，求解等價函數的基本思路為，定義等價函數：

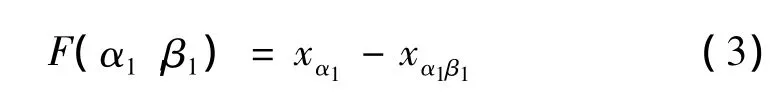
其中：xα1是從負飽和值單調上升到當前值α1時的系統輸出，xα1β1是從 α1值減少至 β1(β1＜ α1)時的系統輸出。遲滯環中，定義上述形式的一次單調升降的曲線為一階轉換曲線(First Order Descending Curves，FOD)，根據SMA絲驅動器的輸入－輸出量設計，曲線形成過程如下：輸入溫度是從零單調增加至設定值α1，然后減少至某個大于零的值β1;“一階”隱含單個曲線成形于系統輸入的一次反向的特點，等價函數則定義為這組曲線的輸出增量。

事實上，如圖6所示，區域S(α1，β1)的積分等于當前值α1和β1的遲滯輸出的差值。

圖6 Preisach理論數值與遲滯曲線的對應關系Fig.6 The relations between hysteresis and Presiach theoretical value

將集合S+(t)劃分成n(t)個梯形點Tk，顯然，結果由式(5)的數學表達式計算，n(t)表示梯形點數量，以時間的函數的形式記錄著動態變化的極值點集合的更新，如圖5中所示。

每個梯形點Tk可表示為兩個三角S(Mk，mk－1)和S(Mk，mk)的差值，其中Mk和mk表示輸入歷史的最大和最小值點，因此，

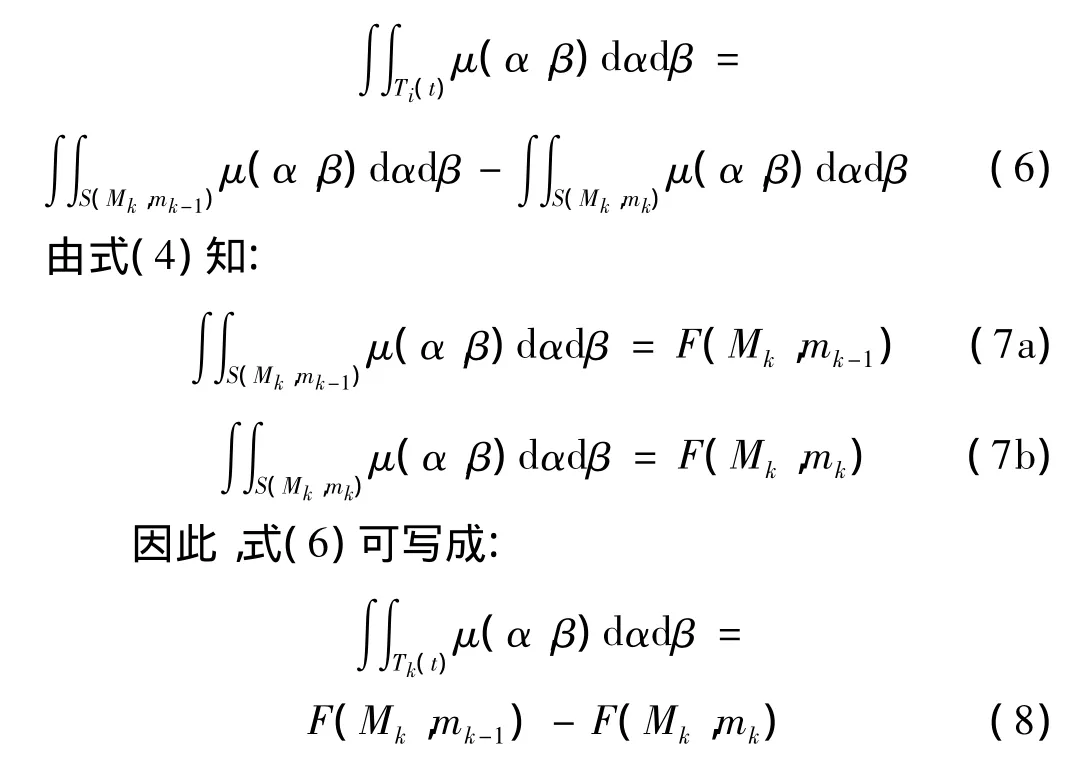
聯立上述表達式，離散的等價函數所表示的遲滯非線性的輸出x(t)為：

需要注意的是，傳統的Preisach模型關于原點對稱，但在SMA絲輸入溫度是高于環境溫度，為正值，與磁性材料不同，不滿足原點對稱性質，需要引入一個偏置項，滿足當系統輸入處于負飽和值時，系統輸出為零。

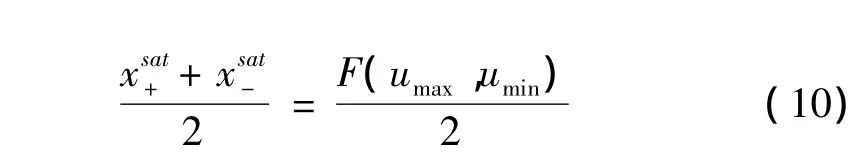
式中：xsat+和xsat－分別表示輸出的極限飽和值，umax和umin分別對應最大和最小的輸入值。

3 仿真試驗

3.1 SMA遲滯模型

根據已有研究，所給出的SMA絲驅動器各變量之間的作用關系如圖7所示，相變機制引起的馬氏體相變，導致SMA材料復雜的熱力學行為［16］。定義馬氏體體積分數(ξ)為內部狀態變量，為外部應力和溫度的作用函數，正逆相變過程中，體積分數的變化函數不同，導致材料的參數變量之間的路徑差異，即遲滯現象，定義溫度與驅動器位移輸出之間的遲滯關系，即是下一節的研究重點，間接反映了SMA驅動器的輸入電流與應變的關系。

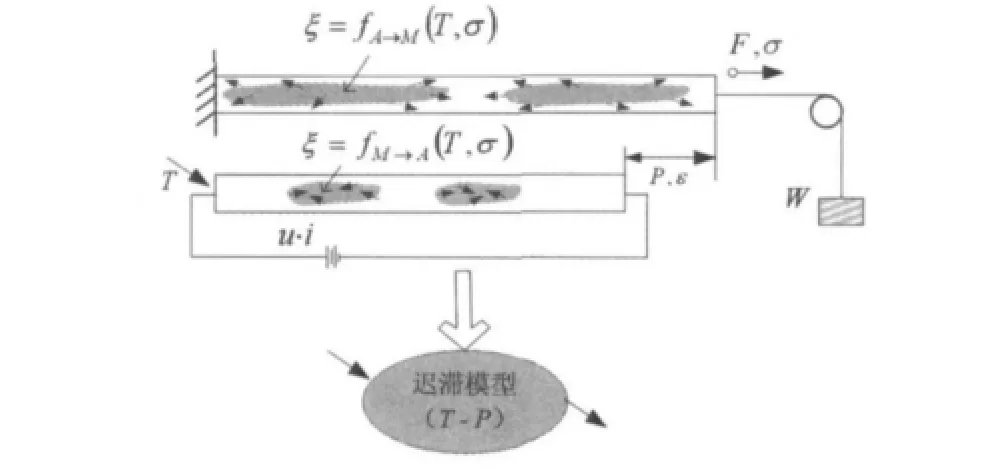
圖7 SMA參數遲滯示意圖Fig.7 Schematic view of hysteresis among SMA variables

3.2 等價函數辨識

文獻［17］提出了從試驗數據決定Preisach權重表面函數的辨識技術。首先，測試得到SMA絲驅動器的輸入輸出數據點集，生成一系列“FOD”曲線;根據SMA絲驅動器的遲滯曲線的主、次環形式，定義辨識函數的參數形式。由一系列數據溫度點，得到的穩態位移輸出數據，形成FOD數據組，通常，所得到的FOD曲線為三維形式，則擬合函數也需滿足三維形式。根據上一節的討論，省略權重函數的辨識環節，直接將Preisach平面分布函數結果，代入遞推式(10)得到遲滯系統的輸出。

根據經驗，指數類型函數可用于FOD曲線的擬合，文獻［18］給出用于表示SMA的主遲滯曲線的指數函數;文獻［19］引用同樣形式的函數得到次遲滯環行為，并取得了很好的匹配效果。Gobert從耗散理論及穩定性角度討論SMA驅動器的遲滯建模及其控制，且基于試驗數據得到多種類型驅動方式下的SMA絲驅動中的Preisach平面函數，較好地描述SMA絲驅動器的非線性遲滯行為，本文引用其中的函數定義式(11)，相關變量和數字定義見文獻［20］。

等價函數是辨識過程的結果，對所需建模的系統執行測試試驗，收集辨識數據。根據SMA絲熱驅動的特點，變化的溫度作為輸入，按照頻率要求，可動態測試驅動器的穩態位移輸出。設計以下的輸入溫度序列：

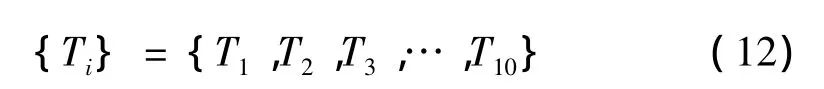
基于溫度的SMA驅動器，可以選擇任意的輸入參考值，如環境溫度。Preisach平面的“零”表示對應這個參考的輸入值，Preisach溫度輸入為T－T∞。由測試數據形成的FOD曲線，如圖8所示，數據曲線的多少由輸入溫度點的設置最大數決定，由一系列FOD曲線，可以得到遲滯系統數值實現的等價函數F(α，β)。

圖8 SMA遲滯建模的辨識函數解釋Fig.8 Explanation of identified functions for SMA hysteresis

圖9 Preisach平面擬合曲面Fig.9 Preisach plane surface fitting

由圖8的FOD曲線形成辨識的離散數據點集，在溫度序列各點形成的穩態位移輸出，構成三維數據點，文獻中根據這個數據點辨識得到圖9的等價函數曲面形式。

3.3 遲滯仿真

根據FOD數據測試試驗和辨識方法得到的等價函數，編制Matlab環境中程序，建立SMA絲驅動器的溫度－位移的遲滯模型如圖10所示。觀察形式如圖10(a)的衰減正弦信號作用下，驅動器的遲滯表現能力，從圖10(b)可以看出，Preisach理論能夠表現系統的遲滯關系，并且充分體現次遲滯環的作用，在建模過程中，省去權重函數的辨識過程，直接利用等價函數，按數值遞推公式(9)構建的遲滯框架是有效的，且引入式(10)中的偏置項，能夠很好解決經典Preisach理論開發的應用于磁性材料的對稱特性，SMA絲驅動器驅動輸入都為正值，且輸入起始點溫度值為T∞以上。

圖10 基于Preisach理論的遲滯模型Fig.10 Preisach－based hysteresis model

4 結論

Preisach理論是一種針對遲滯特性的通用數學工具，本文利用該算子建立了形狀記憶合金作動器輸入溫度與輸出位移關系模型。討論了模型實現方法和建模過程，給出了模型的離散遞推方法，避免了傳統Preisach模型中先求解權系數，以及最后求和計算中的雙積分式，使得計算簡化，便于實際應用中的實時控制。最后采用Robert給出的Preisach平面辨識函數，即等價函數形式，利用Matlab軟件編制遲滯模型程序，表明Preisach模型能較好地模擬記憶合金驅動器的遲滯特性，且說明了次環的作用。

［1］Tan X B，Baras J S.Modeling and control of hysteresis in magnetostrictive actuators［J］.Automatica，2004，40：1469 －1480.

［2］ Tzen J J，Jeng S L，Chieng W H.Modeling of piezoelectric actuator for compensation and controller design［J］.Precision Engineering，2003，27：70－86.

［3］He Y Y.Preisach hysteresis modeling for piezoceramic actuator systems［D］.University of Toledo，Canada，2000.

［4］Zhang W.Modeling and control of magnetostrictive actuator［D］.University of Kentucky，USA，2005.

［5］Kyoung K A，Nguyen B K.Modeling and control of shape memory alloy actuators using Preisach model，genetic algorithm and fuzzy logic［J］.Mechatronics，2008，18：141 －152.

［6］Natale C， Velardi F， Visone C. Identification and compensation of Preisach hysteresis models for magnetostrictive actuators［J］.Physica B，2001，306：161 －165.

［7］Jiles D C，Atherton D L.Theory of ferromagnetic hysteresis［J］.Journal of Magnetism and Magnetic Materials，1986，61(1－2)：48－60.

［8］Davino D，Natale C，Pirozzi S. A fast compensation algorithm for real－time control of magnetostrictive actuators［J］.Journal of Magnetism and Magnetic Materials，2005，290－291：1351－1354.

［9］ Della T E.Preisach modeling and reversible magnetization［J］.IEEE Transactions on Magnetics，1990，26(6)：3052－3058.

［10］ Mayergovz I D，Frienman G.Generalized Preisach model of hysteresis(invited)［J］.IEEE Transactions on Magnetics，1988，24(1)：212－217.

［11］ Nguyen B K，Ahn K K.Feedforward control of shape memory alloy actuators suing fuzzy－based inverse Preisach model［J］.IEEE Transactions on Control Systems Technology，2009，17(2)：434－441.

［12］ Tang Z F，Lü F Z，Xiang Z Q.Hysteresis model of magnetostrictive actuators and its numerical realization［J］.Journal of Zhejiang University Science A，2007，8(7)：1059－1064.

［13］ Gorbet R B，Wang D W L，Morris K A.Preisach model identification of a two－wire SMA actuator［C］.Proceedings of the IEEE International Conference on Robotics＆ Automation，Leuven，Belgium，1998：2161－2168.

［14］ Hong H.Compensation of hysteresis in piezoceramic actuators and control of nanopositioning system ［D］.University of Toronto，Canada，2003.

［15］ Kwan J J，Woo P Y.Hysteresis modeling and compensation in a magnetostrictive actuator［C］.International Conference on Control，Automation and Systems，Seoul，Korea，2008：483－487.

［16］張雨燁，閻 石，Song G B，等.基于Preisach理論形狀記憶合金電阻－應變滯回模型［J］.振動與沖擊，2008，27(8)：146－148.

［17］Mayergoyz I D.Mathematical Models of Hysteresis［M］.Springer－Verlag，New York，1991.

［18］Ikuta K，Tsukamoto M，Hirose S.Mathematical model and experimental verification of shape memory alloy for designing micro actuators［C］.IEEE Micro－Electro－Mechanical Systems Conference，1991：103 － 108.

［19］Madill D R，Wang D W L.The modeling and L2－stability of a shape memory alloy position control system［C］.IEEE International Conference on Robotics and Automation.IEEE Computer Society Press.Los Alamitos，California，1994，1：293－299.

［20］ Gorbet R B.Control of hysteretic systems with preisach representations［D］.Waterloo university，Canada，1997.

Simulation on modeling of temperature-displacement hysteresis in SMA based on Preisach theory

LIU Wang-zhong，CHEN Zhao-bo，HOU Shou-wu，SHEN Na-wei，JIAO Ying-hou
(School of Mechatronics Engineering，Harbin Institute of Technology，Harbin 150001，China)

Smart materials such as shape memory alloys(SMA)are being widely used as actuators and sensors to achieve positioning and active control purposes.However，a major limitation of SMA actuators is their lack of accuracy due to hysteresis.The Preisach theory has emerged as a modeling tool for many smart materials and has recently been applied to the modeling of SMA material systems.The adaptation of the Preisach model to describe the hysteresis behavior of SMA actuator system was discussed and a modified geometric interpretation and numerical implementation method for the classical Preisach model were presented，especially for the hysteresis modeling of SMA actuator system.Finally，one of the assumed functions in Presiach planes given by Gobert was introduced to implement the simulation.Numerical results show that the model can better describe the hysteresis in SMA.

shape memory alloy;Preisach theory;hysteresis;actuator;parameter identification;Matlab code;numerical realization

TH39

A

國家自然科學基金項目(10972065)

2011－01－28 修改稿收到日期：2011－08－03

劉旺中 男，博士，1982年4月生