用電容器的電阻和電容特性公式計算非平行板電容器的電容

葛松華 唐亞明

(青島科技大學數理學院 山東 青島 266042)

許多文章[1～6]對非平行板電容器的電容進行了計算，方法不盡相同，但結論一致，這對教學討論來說是非常有意義的．本文再給出一種方法，就是根據電容器的電阻和電容特性公式，即電容器的漏電電阻R與電容C的乘積等于其間電介質的電阻率ρ與電容率ε之積

RC=ρε

(1)

如果計算出電容器的漏電電阻R，則可得到其電容C，反之亦然.

1 電容器的電阻和電容特性公式

任何兩個導體，無論其形狀、尺寸如何，當它們用絕緣體分隔時，就形成一個電容器，討論電容器的介電性和導電性，就是討論其電容和電阻[7]．

如圖1所示，設一電容器中間充滿各向同性的均勻電介質，其電容率為ε，電阻率為ρ.電源連接在電容器上時，兩導體極板分別帶電+Q和-Q.

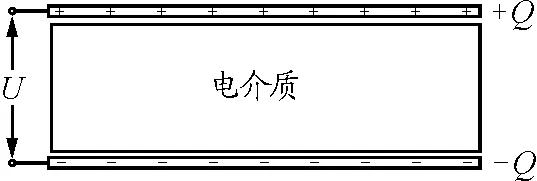
圖1 電容器示意圖

兩導體構成兩個等勢面，其間存在靜電場，兩導體間的電勢差

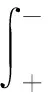
導體上的電荷

Q=?SσdS=?SεEndS=ε?SE·dS

則其電容為

(2)

如果中間的電介質不是理想的絕緣材料，兩導體間將形成通過絕緣材料的電流，則電介質顯示出一定的電阻，這個電阻常稱為漏電電阻，用R表示．

由于兩導體間有電勢差

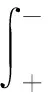
則電介質中的電流

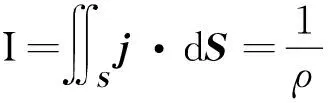
根據歐姆定律，導體間的電阻

(3)

由式(2)和式(3)可得

RC=ρε

上式即為電容器的電阻和電容特性公式，它對所有的電容器都成立．

2 非平行板電容器的電阻和電容

設非平行板電容器兩極板的長為l，寬為L，兩極板延長線交于O點，夾角為θ，其橫截面如圖2所示.極板窄端和寬端到原點O的距離分別為R1和R2,且L=R2-R1,極板的長和寬都遠大于板間距離，可忽略邊緣效應.

圖2 非平行板電容器示意圖

如圖2，在兩極板間r處，取寬為dr的一段圓弧狀的小體積元，該小體積元的面積為ldr、長為rθ，其電阻

兩極板之間的電阻可視為無限多小體積元電阻的并聯，根據電阻的并聯公式可得

則非平行板電容器的漏電電阻

(4)

根據式(1)，得到非平行板電容器的電容

(5)

這與用其他方法所得結果相同.

3 結束語

電容器是電磁學中的一個重要模型，也是電子技術中的一個重要器件，根據電容器的電阻和電容特性，如果知道了電阻可求得其電容，反之亦然，尤其是對一些計算復雜的模型來說，此方法簡單易行．在教學過程中，用此種方法計算或估算一些電磁參數是非常有實際意義的. 另外，在實驗中可以用穩恒電流場的模擬法得到不同模型的電阻值，從而求出其電容[8].

參考文獻

1 鄭民偉.非平行板電容器電容和電場的一種計算.大學物理，2001,20(2)：17～18

2 秦德培.非平行板電容器電容和電場的簡化計算.大學物理，1995,14(1)：13～14

3 李建青，馬爭爭，田旭.非平行板電容器電容和電場的兩種計算方法之討論.大學物理，2008,27(8)：27～28

4 王利敏，李長群，趙雙義.非平行板電容器電容的又一算法.大學物理，2006,25(4)：13～14

5 葛松華.非平行板電容器電場和電容的另一種計算.大學物理，2004,23(11)：34，41

6 鄭民偉.非平行板電容器電場和電容的進一步計算.大學物理，2010,29(12)：10～11

7 賈起民，鄭永令，陳暨耀.電磁學(第二版).北京： 高等教育出版社，2001. 378～379

8 (美)William H.Hayt,(美)Jr. John A. Buck著.徐安士，周樂柱譯.工程電磁學(第六版). 北京： 電子工業出版社，2004. 134～136