課堂交流:貫穿數學課堂的教學主線

　　肖伯納曾說：“你有一個蘋果，我有一個蘋果，我們相互交換蘋果，每人仍然只有一個蘋果。然而，你有一種思想，我有一種思想，我們彼此交換思想，那我們將同時擁有兩種思想。”肖伯納的話對我們在教學中重視課堂交流，尤其是學生之間的交流有很大的啟發。因此，教師要把握好自己的角色，改變傳統的教學行為，關注學生的課堂交流，使學生真正能在交流中相互傾聽、接納、贊賞、分享、互助……
　　一、 平等交流，促使主動學習
　　《求平均數問題》 教學片段：
　　師：第一次來咱們班上課，你們愿意和老師交個朋友嗎？說說你叫什么名字？現在有多高？（學生個別匯報）
　　師：同學們有高有矮，誰能說說我們班同學大概有多高？（學生面面相覷，不知如何回答。這時，教師故意找出班上最高和最矮的同學，欲以他們的身高為班級的代表。）
　　生1：我有意見。他們一個太矮，一個太高。我們班同學的身高應該在他們兩人之間。
　　生2：我認為我們班同學的身高大概與A同學差不多。因為她不高不矮，最接近我們班的中間身高，以她作標準最為恰當。
　　師：有道理！請您猜測一下A同學身高大約是多少？（猜測138厘米，本人證實為136厘米。）
　　師：這個136厘米是我們班每個同學的身高嗎？（不是）那是什么呢？
　　生（齊）：是我們班的平均身高。
　　師：對，要知道我們班同學大概有多高，就是求我們班的平均身高是多少。這節課，我們就一起來研究“平均數”的有關知識。（板書課題）
　　在這個教學片斷中，師生從頭至尾都是在以“相互認識、增進了解”為目的的常態對話中度過的。教師的“我想知道班上學生大概有多高”這一問題一拋，便引發了學生的爭論活動。當學生消除分歧，達成“以A同學的身高為代表”的共識后，教師又問“A同學身高的136厘米是什么”，不僅引出了“平均數”概念，還讓學生對這個概念有了初步的體會，在引發需要的同時，為促成學生對“平均數”意義的實質性理解作好了鋪墊。事實證明，只有通過師生雙方的平等交流，才能促進每一個學生的健康發展，促使學生主動學習。
　　二、 暢所欲言，引發個性遐想
　　《圓的周長》教學片段：
　　師：上節課，我們已經認識了“圓”。你還知道哪些關于圓的知識呢？
　　生1：我知道了怎樣的圖形是圓以及畫圓的方法。
　　生2：我認識了圓心、半徑和直徑，知道半徑和直徑的相互關系。
　　生3：我了解了車輪之所以做成圓形的科學道理。
　　……
　　師：學得不錯！那么，你還想知道哪些關于圓的知識呢？
　　生4：我想知道圓是否也具有像三角形“穩定性”那樣的特性。
　　生5：學長方形、正方形時，要計算周長，所以，我想研究圓的周長。
　　生6：還有圓的面積。
　　師：同學們借助以前學習圖形的經驗，提出了很多富有價值的研究內容。這節課，我們首先來研究“圓的周長”。（揭示課題：圓的周長）
　　導課設計簡潔開放，體現了“以生為本”的理念。無論是舊知識的回顧，還是新問題的提煉，都立足于學生的自主表達。“你已經知道哪些關于圓的知識呢？”觸及了學生已有的認知領域，了解了學生的知識起點，給學生提供了溫習反思的機會。“你還想知道哪些關于圓的知識呢？”則有效地喚起了學生對未知的探索欲望，引發了學生對新課探索主題的個性化遐想，從而有利于學生個性的發展和創新能力的培養。
　　三、 據理力爭，迸發思維火花
　　《商不變的性質》教學片段：
　　讓學生判斷24÷8=（24+24）÷（8+8）是否相等。
　　正方：我們認為它是錯的，因為它的被除數與除數是同時增加，不是同時擴大或縮小的。
　　反方：我們通過計算發現左右兩邊相等的。
　　正方：前面做（60+20）÷（20+20），它的商是變了。
　　反方1：這兩題不一樣，前面是“被除數和除數同時加上同一個數”，而這題“被除數和除數同時加上一個和自己一樣大的數。
　　反方2：我們可以看出：24+24=24×2，8+8=8×2，被除數和除數其實是同時擴大了2倍，商應該不變。
　　師：看來我們不能被表面現象所迷惑，要仔細辨認，弄清它的真實面目。
　　在數學課堂教學中，學生在學習活動中會對某一問題有不同的看法，且各據其理、互不相讓。這時，可讓學生進行爭辯，打破學生舉手、教師點名的老套，鼓勵學生大膽闡明自己的觀點，做到問題不辯不明。提倡“據理力爭”，有利于求得正確的認識、深層的理解，學生在相互交流中極易萌發靈感，發現新知，激活思維的火花，達到“風乍起，吹皺一池春水”的境地。這樣，不僅僅是一種數學方法的傳授，更是一種思想價值的滲透，為學生養成終身學習的習慣打下堅實的基礎。
　　四、 別具一格，彰顯靈動思維
　　《梯形的面積》教學片段：
　　當學生利用兩個完全一樣的梯形拼成一個平行四邊形，推導出梯形的面積公式后，教師準備教學例題（利用公式解決問題）時，
　　生1：老師，我能把梯形剪開嗎？
　　師：當然可以。
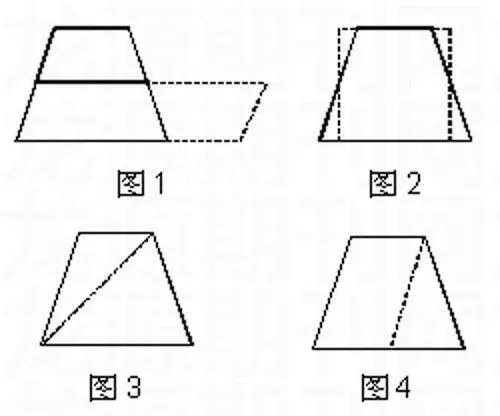
　　生1：那么我只用一個平行四邊形就可以推導出梯形的面積公式。沿兩腰的中點連線剪開，也可以拼成一個平行四邊形（如圖1），平行四邊形的底正好是梯形的上、下兩底的和，高正好是梯形高的一半，因此梯形面積S=(a+b)×h÷2。
　　（教室里響起了熱烈的掌聲。）
　　師：生1同學能從另一個角度思考問題，真了不起，你們還能想出其他辦法嗎？
　　（教室里頓時像開了鍋，同學們思考著、比劃著、議論著，幾分鐘后紛紛舉起了小手。）
　　生2：老師，受生1同學的啟發，我又有一種剪法，我是沿兩腰的中點豎直剪開的（如圖2），正好可以拼成一個長方形，這個長方形的長正好是梯形的上底與下底和的一半，寬正好是梯形的高，因此梯形的面積S=(a+b) ÷2×h = S=(a+b)×h÷2。
　　生3：我們組認為還可以把梯形剪成兩個三角形（如圖3），那么梯形的面積S=a×h÷2 +b×h÷2 = S=(a+b)×h÷2。
　　（正當全班同學為自己的創造性勞動感到高興時，教師發現生4同學站起來又坐下，欲言又止，這時，教師及時請她發表了自己的觀點。）
　　生4：我是把梯形剪成一個平行四邊形和一個三角形（如圖4），那么梯形的面積應該是三角形的面積加上平行四邊形的面積，即S=a×h+(b-a)×h÷2 ，可是下面我不知道怎么辦了。
　　師：同學們，你們認為生4的這種方法可行嗎？咱們能共同想辦法解決嗎？
　　（同學們經過討論后認為辦法是可行的，并說出了自己的想法。）
　　數學教學要培養學生的創新精神和實踐能力。在上述教學中，教師鼓勵學生從“新”的角度去思考，提出了有個性、有創意的推導方法，避免了學生的思維定勢，訓練了學生動腦、動口和動手的能力，培養了學生不迷信、不盲從、獨立質疑的探索精神。我們的學生是鮮活的，他們的思維是靈動的。只要給學生一個空間，他們就會自己往前走，在智慧與智慧碰撞中，在思想與思想交流中，他們會慢慢地學會起飛，他們的生命活動也因此更精彩。
　　此文獲2010年浙江省規劃課題一等獎（節選）