教師如何讓數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中綻放

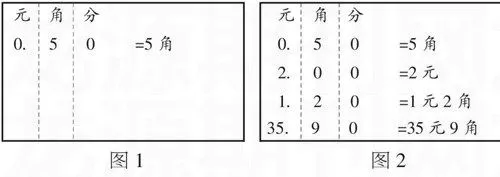
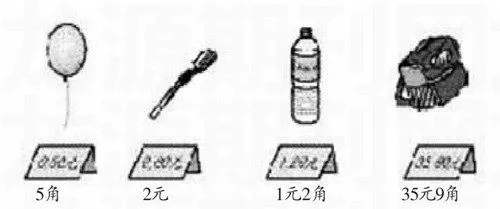
　　筆者曾經(jīng)聽(tīng)過(guò)這樣一節(jié)課：一位教師在教學(xué)“認(rèn)識(shí)物品價(jià)格”一課時(shí)，出示了四種不同的商品價(jià)格圖，然后問(wèn)學(xué)生：“你們知道這些商品價(jià)格是幾元幾角嗎？”有一位學(xué)生回答道：“0.50元表示5角。”教師又問(wèn)：“你是怎么懂得是5角的？”“小數(shù)點(diǎn)左邊的數(shù)是元，小數(shù)點(diǎn)右邊的第一位是角，第二位是分。”“對(duì)了！”接著，教師就用事先準(zhǔn)備好的小黑板掛在上面，領(lǐng)著學(xué)生齊讀三遍：小數(shù)點(diǎn)左邊的數(shù)表示幾元，小數(shù)點(diǎn)右邊的第一個(gè)數(shù)表示幾角，第二個(gè)數(shù)表示幾分。然后在四種物品標(biāo)價(jià)下面相應(yīng)地寫出：5角、2元、1元2角、35元9角（如下圖所示）。
　　例題教學(xué)就這樣結(jié)束了，在后面的練習(xí)中，出現(xiàn)了這樣的現(xiàn)象：4.10元表示4元10角，19.00元表示1元9角……課后，這位教師反思時(shí)提出了疑惑：為什么讀那么多遍結(jié)語(yǔ)學(xué)生仍不理解呢？
　　案例中的問(wèn)題讓我陷入深思：在教學(xué)中，數(shù)學(xué)知識(shí)是一條明線，得到數(shù)學(xué)教師的重視；數(shù)學(xué)思想方法是一條暗線，卻被我們教師忽視了。在平時(shí)的教學(xué)中，為了走捷徑，教師不是很好地通過(guò)數(shù)與形的有機(jī)結(jié)合讓學(xué)生充分理解，掌握其中的基本數(shù)量關(guān)系，而是讓學(xué)生機(jī)械地記憶：解答比多比少應(yīng)用題時(shí)， 求“大數(shù)”用加法，求“小數(shù)”用減法；解答分?jǐn)?shù)應(yīng)用題時(shí)，單位“1”已知用乘法，單位“1”未知用除法或方程；解決幾何圖形問(wèn)題時(shí)，生搬硬套公式解題……結(jié)果使得學(xué)生的解題活動(dòng)完全建立在機(jī)械記憶和對(duì)例題、公式應(yīng)用的簡(jiǎn)單模仿上，如果碰到稍復(fù)雜的題目，學(xué)生就無(wú)從下手，導(dǎo)致學(xué)生解決綜合問(wèn)題的實(shí)際能力差。而新課程要求我們每位教師要從根本上改變教學(xué)方法，強(qiáng)化數(shù)學(xué)思想方法的教與學(xué)，培養(yǎng)學(xué)生運(yùn)用數(shù)學(xué)思想方法的意識(shí)和能力，鍛煉學(xué)生的思維品質(zhì)，提高課堂教學(xué)的有效性。因此，轉(zhuǎn)變教師觀念，讓教師系統(tǒng)地運(yùn)用數(shù)形結(jié)合思想進(jìn)行數(shù)學(xué)教學(xué)是目前我們面臨的一個(gè)極富實(shí)踐價(jià)值的重要課題。那教師怎樣才能使數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中綻放呢？
　　一、教師要了解數(shù)形結(jié)合思想的深遠(yuǎn)意義，樹立加強(qiáng)數(shù)學(xué)思想方法學(xué)習(xí)的意識(shí)
　　數(shù)形結(jié)合是我國(guó)傳統(tǒng)數(shù)學(xué)的基本思想方法之一，在數(shù)學(xué)教學(xué)歷史中具有舉足輕重的地位。縱觀一年級(jí)到六年級(jí)數(shù)學(xué)教材的編排意圖，都充分體現(xiàn)著數(shù)與形的有機(jī)結(jié)合的思想，以幫助學(xué)生從直觀到抽象，逐步建立起整個(gè)數(shù)學(xué)知識(shí)體系，培養(yǎng)學(xué)生的思維能力。因此，作為小學(xué)數(shù)學(xué)教師，要加強(qiáng)數(shù)學(xué)思想方法的學(xué)習(xí)，深刻領(lǐng)會(huì)“數(shù)形結(jié)合”的內(nèi)涵，樹立“數(shù)形結(jié)合”的意識(shí)，使自己在今后的教學(xué)中注重“數(shù)形結(jié)合”思想的滲透，引導(dǎo)學(xué)生嚴(yán)密思維，靈活思考，善于抓住事物的主要矛盾，使學(xué)生學(xué)會(huì)有效的思維方法，從而促進(jìn)學(xué)生數(shù)學(xué)能力的提高。
　　二、指導(dǎo)教師運(yùn)用數(shù)形結(jié)合思想設(shè)計(jì)教學(xué)，形成“數(shù)形結(jié)合”教學(xué)模型
　　數(shù)形結(jié)合方法的實(shí)質(zhì)是將抽象的數(shù)學(xué)語(yǔ)言與直觀的圖形結(jié)合起來(lái)，其具有雙向性，有以“形”助“數(shù)”和以“數(shù)”解“形”兩個(gè)特點(diǎn)。在聽(tīng)課調(diào)研中，我們發(fā)現(xiàn)很多教師不掌握數(shù)形結(jié)合思想的運(yùn)用方法，因此我們要利用好課堂教學(xué)這平臺(tái)，或是加強(qiáng)數(shù)形結(jié)合方法的個(gè)案指導(dǎo)，或是利用課例研討、交流的形式，最后形成一種教學(xué)模式，以便供教師們學(xué)習(xí)、運(yùn)用。如我在課后就給案例中的這位教師提出這樣一個(gè)建議：利用數(shù)形結(jié)合的思想教學(xué)。即結(jié)合學(xué)生的回答，出示如圖1所示的板書，然后在0.50元下面相續(xù)寫出2.00元、1.20元、35.90元，讓學(xué)生看著板書嘗試進(jìn)行等價(jià)轉(zhuǎn)換（如圖2所示）。這樣通過(guò)數(shù)與形的一一對(duì)應(yīng)的理解，學(xué)生定會(huì)比反復(fù)讀結(jié)語(yǔ)易于理解、接受。
　　三、考評(píng)中體現(xiàn)出數(shù)形結(jié)合思想的運(yùn)用，發(fā)揮“數(shù)形結(jié)合解決問(wèn)題”的優(yōu)勢(shì)
　　在小學(xué)數(shù)學(xué)教學(xué)中，培養(yǎng)學(xué)生的能力是最終