不確定性修正的相似性測度關聯算法

黃偉平， 徐 毓， 王 杰

(1.空軍雷達學院，a.研究生管理大隊; b.科研部，武漢 430019; 2.中國人民解放軍95174部隊，武漢 430019)

0 引言

分布式系統結構由于對信道容量要求低、生命力強、在工程上易于實現而得到很大重視。在分布式結構的信息融合系統中，每個傳感器都有自己的處理器，形成局部航跡，再在融合中心對各局部航跡進行分配組合，形成系統航跡。在此過程中的航跡關聯算法通常有基于統計［1－2］和模糊數學［3］的方法兩大類。相似性測度的航跡關聯算法是典型的基于模糊數學的方法，該方法基于模式識別思想提出［4］，將各傳感器中的任意航跡視為一個模式，把航跡關聯問題轉化為模式匹配問題，根據航跡整體走向判斷相關性，完成對各局部航跡的分配，關聯效果較好［5］。

但是，由于傳感器對目標跟蹤具有信息的不完整性、不準確性，并存在虛情和漏情，而且目標及其存在環境的諸多信息也難以為數據關聯所充分掌握或應用，每個時刻各航跡的相似性測度會存在一定的誤差［6］，也就是說，航跡關聯判決所依據的統計量不都是可靠的，存在不確定性。“航跡相似性測度”及其“航跡關聯不確定性”都是航跡關聯信息的重要組成部分［7］，它們共同構成完整的航跡關聯信息。在航跡關聯不確定性方面，Blackman［8］定性地將跟蹤關聯問題空間劃分為3個區域:正確關聯區域、不穩定區域和錯誤關聯區域。因此，在相似性測度的計算中，獲取航跡關聯對的不確定性描述，以判定兩條航跡產生于同一個目標的可疑程度，并對航跡對的關聯相似性測度進行修正，對提高情報融合系統的自適應能力和精確性具有一定的應用價值。

本文將對引起航跡關聯對不確定性的因素進行分析，并構造相應的修正因子以表示多條航跡關聯對來源于同一個目標的可疑程度。在關聯判決中，利用不確定性因子對航跡關聯對的相似性測度進行修正，以減小不確定因素對航跡關聯的不利影響。本文算法的研究路徑為:首先，計算各航跡間的歸一化相似性測度，采用相似性測度閾值條件來挑選航跡關聯對，形成待確定航跡關聯對;接著，評價作為關聯決策依據的航跡整體相似性測度計算過程中的不確定性;然后，分析引起航跡關聯不確定性的因素，根據各不確定性因素，計算相應的修正因子;進而，基于修正因子對航跡相似性測度進行修正，利用修正的相似性測度極大化條件，確認最終的正確關聯組合。

在航跡關聯中，增加航跡關聯不確定性分析環節，利用關聯不確定性因子對航跡關聯相似度進行修正，利用修正的航跡相似性測度作為關聯判斷統計量，能有效減小系統誤差參數、虛情或漏情等不確定因素對航跡關聯的不利影響，得到更低錯誤關聯率，仿真實驗驗證了算法的有效性及可靠性。

1 模式識別的航跡關聯

設傳感器i跟蹤ni個目標，其航跡號集合為?i={1，2，…，ni}，在時間t上對第p個目標的狀態估計形成的航跡為Xip(t)，p∈?i，估計誤差協方差為vip(t);傳感器 j跟蹤 nj個目標，航跡號集合為 ?j={1，2，…，nj}，對第q個目標的狀態估計形成的航跡為Xjq(t)，q∈?j，估計誤差協方差為vjq(t)，且兩傳感器誤差獨立。

1.1 關聯步驟

1.1.1 待關聯航跡

在傳感器i和傳感器j共同探測區域內，以待關聯航跡Xip(t)為中心，取一個適當大小的連通區域，并以U表示該區域內所有航跡的集合。定義時間t上待關聯航跡集合為:A(t)={(Xip(t)，Xjq(t))|Xip(t)∈U，Xjq(t)∈U};傳感器i、傳感器j的待關聯航跡集分別為

在數據關聯看來，一個航跡通常與另一傳感器的多條航跡、而不是僅與一條航跡有相關的可能性。多傳感器航跡關聯關系可以用關聯矩陣表示:

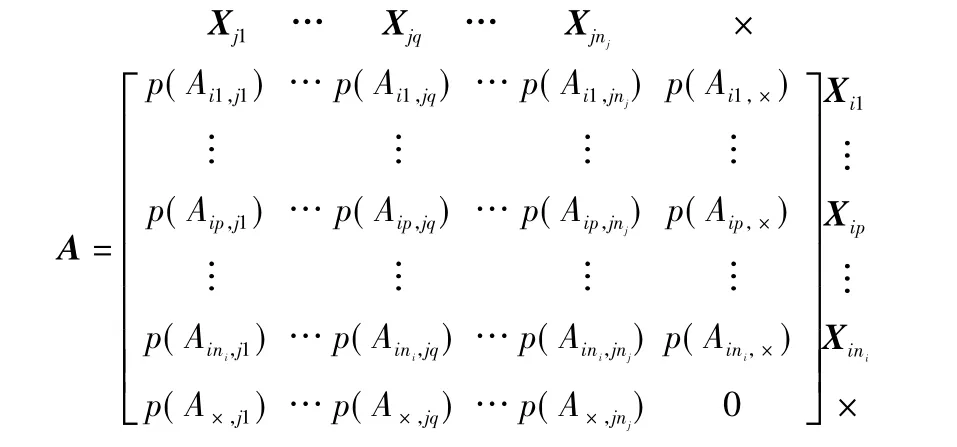
其中:×表示不存在的航跡;Aip，jq表示航跡Xip和航跡Xjq來源于同一個目標(或虛警)的事件;Aip，×表示Xip不對應于另一傳感器的任何航跡的事件;p(Aip，jq)表示事件Aip，jq發生的概率，在基于模式識別的航跡關聯算法里，p(Aip，jq)即為相似性測度 aip，jq。

1.1.2 統計距離

定義 rip，jq(k)=Xip(k) － Xjq(k)，其維數為 N。假設rip，jq(k)服從高斯分布，則其協方差矩陣為v(k)的各元素為

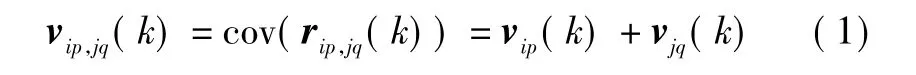
定義Xip(t)、Xjq(t)兩航跡在k時刻的統計距離為

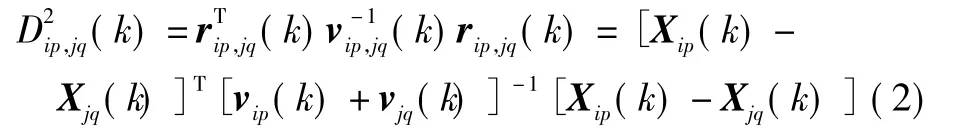
1.1.3 航跡總體相似性測度

定義在k時刻的模式相似性測度為

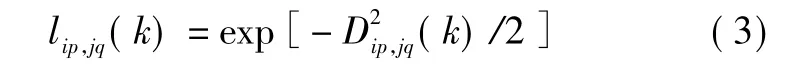
其意義是:在k時刻航跡間的距離越小，則數據間的相似性測度越大。故把1～(k－1)時刻的航跡相似性測度組成航跡相似性向量:

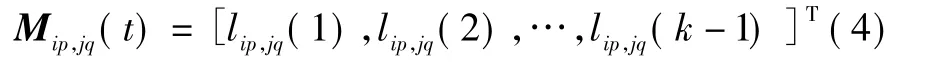
則航跡Xip(t)與航跡Xjq(t)到k－1時刻為止的總體相似性測度［5］為

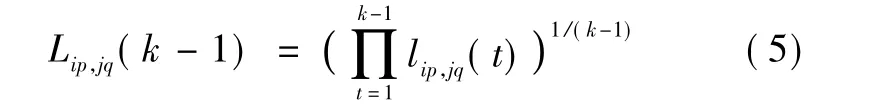
進而得到下面遞推式

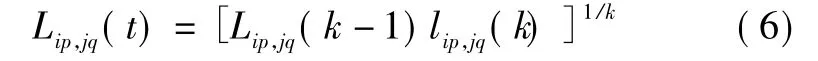
1.1.4 歸一化航跡相似性測度

分別計算Xip(t)與集合Aj(t)中每一個航跡的相似性測度，并構成向量:

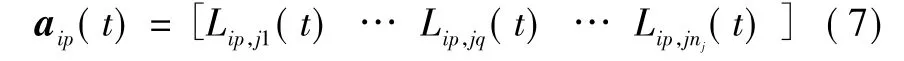
定義歸一化航跡相似性測度

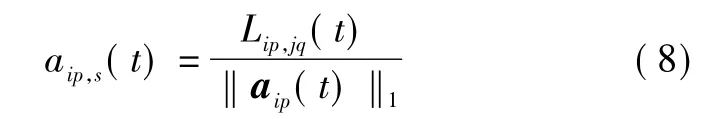
式中:‖aip(t)‖1表示向量aip(t)的1－范數。

1.1.5 待確認航跡關聯對

在航跡間總體相似性測度的基礎上，采用相似性測度閾值條件來挑選航跡關聯對。即若

1.2 性能分析

事實上，在時間t上傳感器i和傳感器j的兩航跡Xig(t)和Xjh(t)來源于同一真實目標(用T標識)概率為

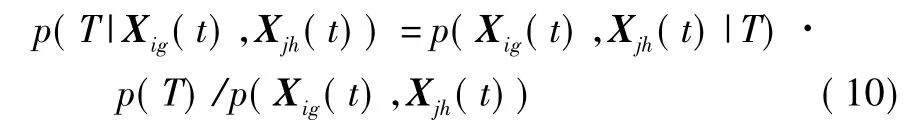
則其概率密度函數為

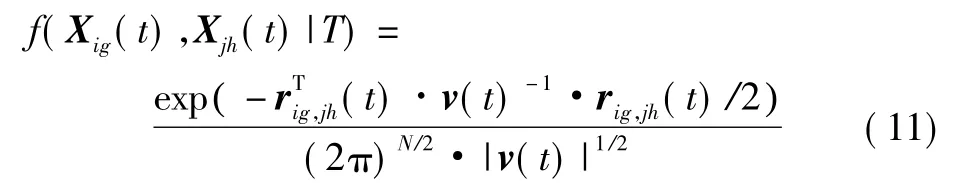
在基于模式識別的數據關聯算法中，通常將Xig(t)和Xjh(t)的相似性測度Lig，jh(t)定義為f(Xig(t)，Xjh(t)|T)，并以之作為關聯判決的依據。

式(10)、式(11)說明，航跡Xig(t)和Xjh(t)來源于同一真實目標的概率不僅與Lig，jh(t)或p(Xig(t)，Xjh(t)|T)有關，還與反映目標的存在與分布情況、反映傳感器的探測性能的p(T)、p(Xig(t)，Xjh(t))有關。可見，基于每個時刻Lig，jh(t)作出關聯決策的航跡整體相似性測度，其關聯航跡并不一定以較高概率來源于同一真實目標，需要對航跡的相似性測度進行修正。

2 引起航跡關聯不確定性的因素分析

航跡在某時刻相似性測度的不確定性產生于傳感器對客觀世界感知的不完全性。傳感器對目標探測信息的不完整、不精確、不準確，信源存在虛情、漏情及探測范圍受限，以及傳感器工作特征參數未確知等因素，造成一個傳感器探測的某一航跡與另一傳感器的零條或多條航跡的不確定區域出現重疊，使得航跡的關聯存在多種可能性，從而導致關聯決策具有必然的不確定性［9］。下文就引起關聯不確定性的幾種情況進行分析。

2.1 傳感器的未檢測區域

一個傳感器對某一目標的感知不確定區域與其他傳感器未感知區域存在重疊關系，會導致航跡關聯存在不確定性。圖1示意的是電子偵察E1與雷達R1構成的探測系統。由于電子偵察的感知范圍往往大于雷達的感知范圍，電子偵察偵測的輻射源不一定位于雷達的探測范圍內，即便存在雷達探測目標T1、T2與輻射源Tb的方位線相距很近，判定Tb與T1或T2關聯顯然是不正確的。

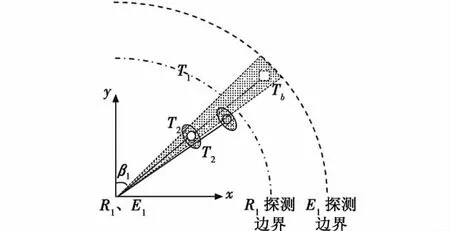
圖1 傳感器未感知區域導致的關聯不確定性Fig.1 The uncertainty brought by the undetective area of the sensor

2.2 傳感器的漏情和虛情

傳感器都有一定的虛、漏情率，可按漏情率虛擬出若干個航跡作為漏情，任一航跡信息都可能是虛情，傳感器的漏情和虛情也是引起航跡關聯不確定性的重要因素。

2.3 傳感器參數的未確知性

當對傳感器的系統誤差參數不確切掌握，而僅知道其范圍的情況下，通常用常值隨機過程來描述傳感器各獨立測量方向的系統誤差。圖2示意的是傳感器R2存在較大的系統誤差且其參數未知的情況。系統誤差使得傳感器的目標感知不確定區域變大、且航跡明顯偏離目標的真實狀態，從而導致不同傳感器對不同目標(如Ta與T2)的感知不確定區域出現重疊，造成航跡關聯問題復雜化。因此，在分析引起關聯不確定性因素的過程中，有必要區分傳感器的系統誤差和隨機誤差的影響［1－2］。

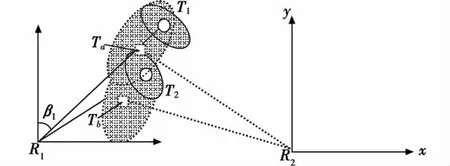
圖2 傳感器系統誤差和目標密集分布導致關聯不確定性Fig.2 The uncertainty brought by system error of the sensor and dense distribution of the target

2.4 目標信息的不準確性

由于傳感器具有不同分辨率，在實際工作存在缺維探測等現象，因此，vip，jq(t)的取值存在一些誤差，從而影響統計距離的準確性，這也將增加相似性測度的不確定性。

圖3所示的是兩個二維雷達對兩個空中目標探測的情況。圖中，β表示目標的方位，ε表示目標的仰角。由于二維雷達不能提供目標仰角信息，使得兩個雷達R1、R2對兩個目標的感知不確定區域互相重疊，造成航跡關聯環節沒有充分的信息判定兩個目標的相對位置關系(T1、T2情況下的等高關系或Ta與Tb情況下的高低關系)，導致關聯判別存在很大的不確定性。

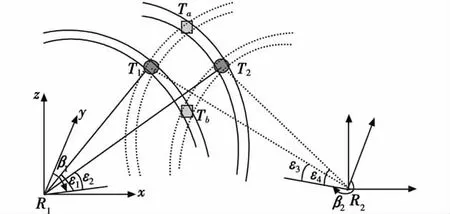
圖3 缺維探測導致的關聯不確定性Fig.3 The uncertainty brought by the incomplete detection

圖4 示意的是兩個具有不同分辨率的雷達對水面目標的感知情況。將雷達R1與雷達R2感知的目標信息進行關聯時，若按照傳統的一對一關聯的原則，無論是將Ta分配給T1還是T2都是不恰當的，都存在較高的關聯不確定性，都將對后續的融合處理產生負面影響。

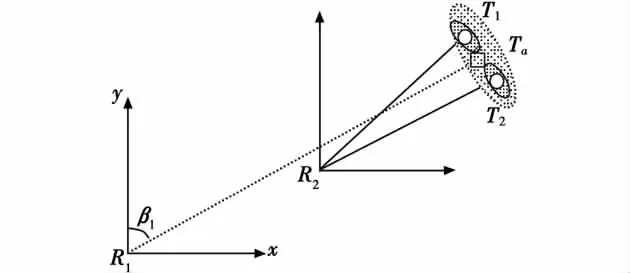
圖4 不同分辨率導致的關聯不確定性Fig.4 The uncertainty brought by the unmatched resolving power

3 修正的航跡關聯相似度

分析傳感器探測的目標探測性能對航跡關聯判決的影響，計算兩傳感器各航跡間的不確定性修正因子，以去偏差后的統計距離用于描述航跡的相似性測度，綜合虛情、漏情等多傳感器探測信息的不一致性對航跡關聯判決的影響，形成航跡關聯相似度的修正值，確認最終的航跡的關聯對。

3.1 描述未檢測區域

假設以狀態空間中的一個連通區域Ω來表示傳感器對目標測量的不確定性。若傳感器i對目標p的探測不確定區域不完全被傳感器j的探測范圍覆蓋，以Ωip表示傳感器i對目標p的探測不確定區域，以Ωip，j表示 Ωip被傳感器 j的探測范圍所覆蓋的部分，以表示目標在 Ωip條件下落入 Ωip，j的概率，則定義傳感器j關于航跡Xip(t)未檢測區域的計算因子

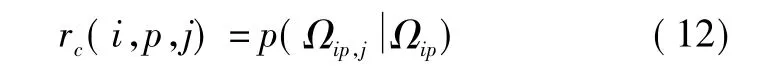
該值可以根據傳感器探測指標及相對位置估算。

3.2 描述漏情、虛情的修正因子

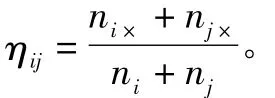
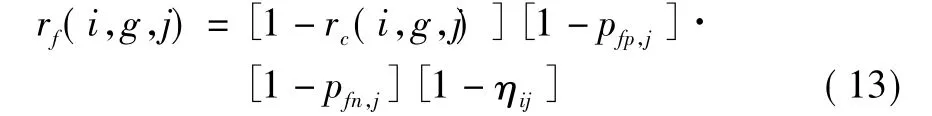
3.3 修正傳感器系統誤差

定義

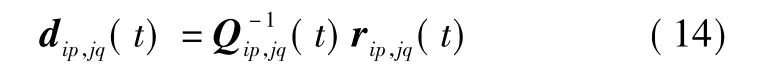
對集合Ac中的傳感器i和傳感器j的待確認關聯對集合 Ad={(Xig，Xjl))|l∈aj}，其中其元素的個數為nd，采用式(14)統計偏差矢量dl(t)，其中，l=1，2，…，nd，構成統計偏差矢量集合:

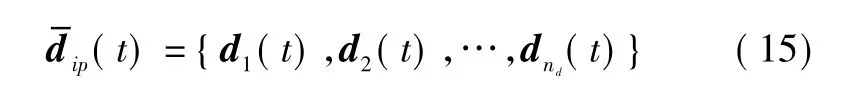
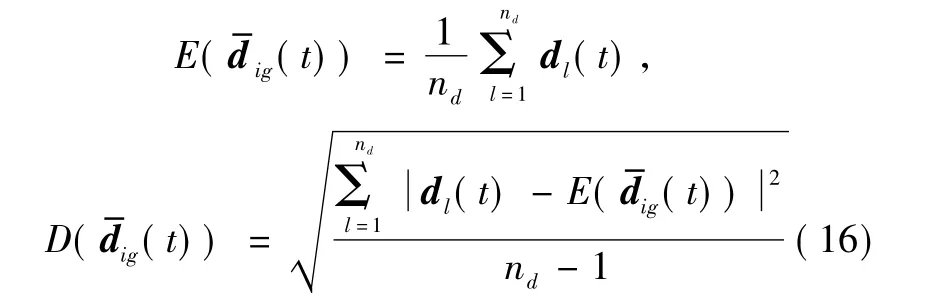
通過對待確認關聯航跡對的統計偏差分析能克服傳感器系統誤差對關聯統計距離的影響。

3.4 修正的相似性測度

基于式(14)、式(16)定義Xig(t)的修正統計距離

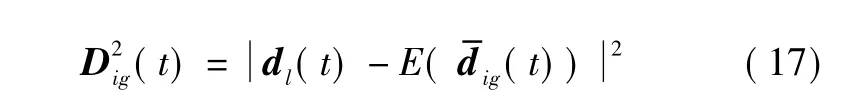
將修正后的統計距離代入式(3)～式(8)，得到修正的相似性測度 aig，s(t)，同樣的，可以計算 as，jh(t)。結合式(13)、式(17)，形成兩航跡 Xig(t)、Xjh(t)關聯相似度修正模型［10］:

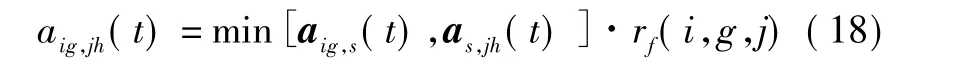
4 關聯確認

在閥值挑選尋找出來的待確認航跡關聯對集合Ac的基礎上，采用相似性測度最大化的準則來確認航跡關聯的判斷。即若

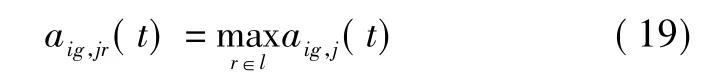
則判斷航跡Xig(t)與航跡Xjr(t)在時刻k相關。且航跡Xig(t)不再與aj中其他航跡相關，對應的航跡Xjr(t)亦不再與ai中其他航跡相關，將航跡Xig(t)，Xjr(t)從待確認航跡關聯集中去掉，繼續下一條航跡的確定，直至全部航跡關聯完畢。

5 仿真驗證

模擬2部雷達對5批空中飛行目標進行探測的場景，目標雷達、目標的位置及編號如圖5所示。在仿真實驗中，雷達在各獨立測量方向上的誤差模型為

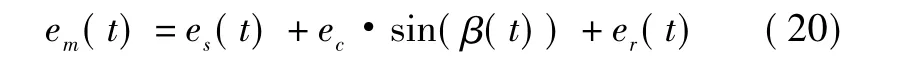
其中:es(t)為常值系統誤差項;ec為周期性系統誤差的幅度;β(t)表示目標的方位;er(t)為隨機誤差項。兩個雷達的距離ec均取為60 m，方位ec均取為0.3°，距離er(t)的標準差均取為40 m，方位er(t)的標準差均取為 0.2°。

圖5 雷達和目標分布示意圖Fig.5 The distribution of the sensor and the target

從圖6、圖7可以看出，基于相似性測度的航跡關聯算法對目標航跡的關聯均能取得較低的錯誤率，但修正的關聯算法由于考慮到目標關聯過程的不確定因素，通過各不確定因子的修正，錯誤關聯率更低，能取得更好的關聯效果。

圖6 相似性測度的關聯錯誤率Fig.6 The false probability of the similarity degree method

本文提出的修正航跡關聯算法，一方面基于航跡相似性測度計算過程中的不確定性因素，對作為關聯依據的統計量進行了修正;另一方面，在航跡關聯對匹配的過程中，采用閥值初選和極大值確認兩個環節進行關聯確認，航跡關聯的錯誤率也隨之降低，說明本文采用的相似性測度修正方法是有效且實用的。

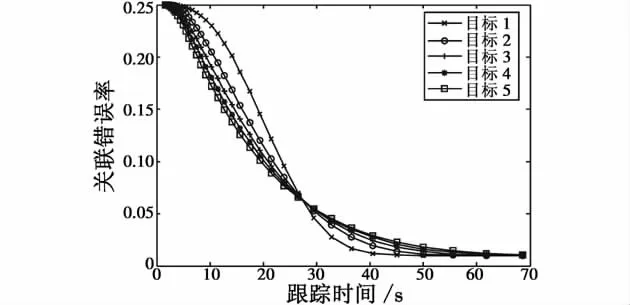
圖7 修正的相似性測度的關聯錯誤率Fig.7 The false probability of the modified similarity degree method

6 結論

本文提出的修正航跡關聯算法，以歸一化航跡相似性測度為基礎，綜合考慮傳感器的虛情、漏情、未檢測區域以及傳感器參數的未確知性等因素對航跡相似性測度關聯的不利影響，對航跡關聯相似性測度進行了修正。在航跡關聯過程中，先采用閥值挑選出待確認航跡關聯對，通過對待確認航跡關聯對的統計分析，計算出引起航跡對不確定性因素的影響因子，用這些影響因子得到新關聯統計量——修正的相似性測度，結合相似性測度極大化確認最終的航跡關聯組合。仿真實驗表明，修正的航跡相似性測度關聯算法能得到目標更低的關聯概率，為提高系統航跡的魯棒性、精確性奠定了基礎。

［1］ 孫俊生，王建民，王維鋒.多傳感器多目標聯合概率數據關聯研究［J］.信號與信息處理，2009，39(11):19-21.

［2］ 楊哲，韓崇昭，李晨，等，基于目標之間拓撲信息的數據關聯方法［J］.系統仿真學報，2008，20(9):2357-2360.

［3］ 胡傲，馮新喜，王冬旭，等.遺傳模糊聚類算法在數據關聯中的應用［J］.電光與控制，2010，17(3):30-34.

［4］ 蔡元龍.模式識別［M］.西安:西安電子科技大學出版社，1992.

［5］ 黃偉平，徐毓，王杰.綜合運用模式識別與回歸分析的數據融合算法［J］.控制與決策，2010，25(1):110-115.

［6］ BAR-SHALOM Y，BLAIR W D.Multitarget-multisensor tracking applications and advances［M］.London:Artech House，2000.

［7］ KLIR K G.Uncertainty and information:Foundations of generalized information theory［M］.Hoboken:John Wiley ＆ Sons，Inc.，2006.

［8］ BLACKMAN S.Multiple target tracking with radar applications［M］.Norwood，Ma:Artech House，Inc.，1986.

［9］ 林洪樺.測量誤差與不確定度評估［M］.北京:機械工業出版社，2010.

［10］ BAR-SHALOM Y，CHEN H.Multi-sensor track-to-track association for tracks with dependent errors［C］//The 43th IEEE Conference on Decision and Control，Paradise Island，Bahamas，2004:2674-2679.