基于模糊奇異攝動模型的直接型自適應控制器的設計

李 莉， 孫富春， 裴衛東

(1.天津師范大學計算機與信息工程學院，天津 300387;2.清華大學計算機科學與技術系人工智能重點實驗室，北京 100084)

0 引言

由于存在強的柔性模態，帶撓性附件航天器可以用含小攝動參數的多時標非線性系統進行描述。由于多時標系統中病態問題的存在，對其建模與控制比較困難。以往的處理方法通常是忽略較小的時間常數，對近似模型進行分析和綜合［1－4］。這種方法實際上是僅對系統中呈慢變化部分的狀態變量保留了小參數的零階近似，而對系統中呈快變化部分的狀態變量，不僅忽略了其小參數的高階近似，也使得它在邊界層內的值丟失了主要項，達到失真的程度。采用這種方法設計控制器，雖然能夠降低控制器的階次和簡化其結構，但是往往不能滿足系統的性能要求，甚至會導致閉環系統不穩定。

由于奇異攝動理論能夠描述帶有小參數的高階微分方程，從20世紀60年代末到70年代初開始，用奇異攝動理論來研究、討論多時標系統的分析和綜合問題成為這一領域的主要方法并逐漸發展成熟。但是現有的控制策略都需要奇異攝動系統的模型已知，而且多用于線性系統，這在工業領域有時候很難達到。既然智能控制理論如模糊集和神經網絡理論已經成功用于許多具有不確定性和建模誤差的實際系統［5－6］，它們同樣可以用于模型部分或全部未知的奇異攝動系統控制中。

孫富春及其課題組最早提出了一種模糊奇異攝動模型并在此領域開展了一系列研究工作［7－9］。在給出模糊奇異攝動模型的定義的基礎上，進行了當攝動參數足夠小時的閉環穩定性分析，并提出了鎮定并行分布式補償控制器，對連續或離散系統，其控制器增益可以分別歸結為一組LMI或BMI，后者可以利用迭代LMI方法有效地求解。鑒于模糊奇異攝動模型能夠將多時標非線性系統通過隸屬函數轉變為一系列多時標線性系統的插值，適用于多時標線性系統的方法可以通過適當的變化用于非線性奇異攝動系統中。為減少LMI或BMI方法求解控制器的保守性問題，提出一種基于模糊奇異攝動模型的自適應控制器，用于存在不確定性的帶撓性附件航天器的跟蹤控制中，采用Lyapunov方法保證閉環系統的穩定性。仿真結果證明，所設計的控制器能夠獲得較好的跟蹤效果［10－12］。

以上提出的控制方法，絕大多數要求模糊奇異攝動模型的規則后件或者部分或者完全已知，這在實際系統中，有時很難達到。為此，本文將進一步深化研究奇異攝動系統的控制問題。當模糊奇異攝動模型的規則后件參數完全未知時，提出一種直接型自適應控制器，其中狀態反饋的增益可以在線調整。最后將此控制器用于后件參數未知的模糊奇異攝動系統的模型跟蹤控制中，并與初始條件及參考模型相同但后件參數已知情況下設計的魯棒控制器相比較，仿真結果證明了該自適應控制器的有效性。

1 問題闡述

設一大類奇異攝動系統如柔性機械手能夠由以下數學模型進行描述:

其中:ri是子系統的相對階rp+1=2。x(t)和z(t)分別是快慢狀態向量;x(t)=和為控制輸入;fi(x，z)，gij(x，z) 為未知函數;ε是小的正數。

(1)可以寫成

系統(1)、系統(2)可以建立由一系列“如果－則”規則描述的模糊奇異攝動模型。假設第l條規則如下。

Rl:如果v1是且…且vN是ΨlN，則

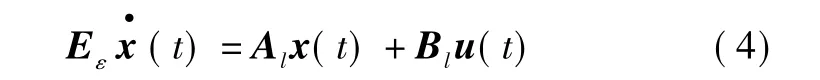
給定輸入輸出對x(t)和u(t)，TS模型可以合成為

這里xm(t)∈Rn表示參考模型的狀態，r(t)∈Rp為有界參考輸入。

定義跟蹤誤差為

控制目標即設計控制器u(t)，使得被控對象的狀態x(t)跟蹤穩定參考模型的動態xm(t)，即當t→∞時，e(t)→0。

2 自適應控制器設計及穩定性分析

由于矩陣Hl和Ll未知，假設此時的理想控制律為

則可得閉環系統為

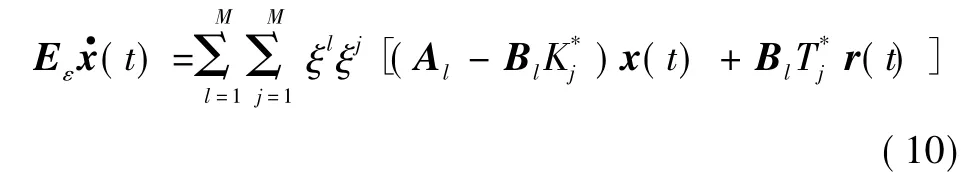
則閉環系統等價于式(7)，因為式(7)為穩定系統，則有當t→ ∞ 時，e(t)→0。

對式(8)求導得

將式(12)代入式(13)，可得

則有

所以式(14)即為

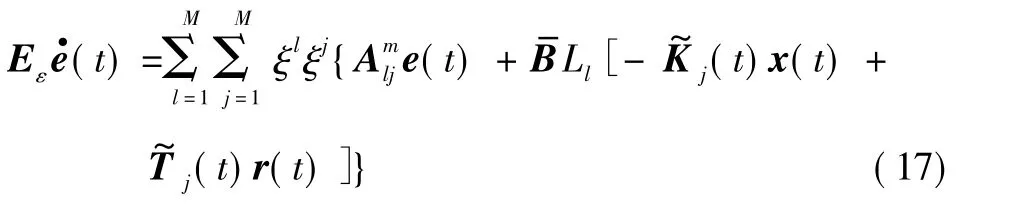
對式(18)求導得

取自適應律為

將式(21)、式(22)代入式(20)得

由此得到定理1。

定理1考慮式(3)所示的被控系統和穩定參考模型(6)，采用控制律(12)和自適應律(21)、(22)，假設參考輸入r(t)和參考狀態量xm(t)一致有界，則能夠保證在控制量和輸入信號有界的情況下，當t→∞時，e(t)→0。

證明:由式(23)得，對于任意的 t＞0，有 e(t)，有界。因為xm(t)有界，則X(t)有界。又因為r(t)∈L∞，根據式(12)得u(t)∈L∞。因此閉環系統的所有信號有界。所以

由式(23)可以得到

因此有e(t)∈L2。

由于小參數ε的存在，在求解LMI的過程中會存在病態。可以令式(19)變化為不等式

只要使得公共矩陣P滿足式(26)

討論:設計參考模型(6)的首要條件是穩定，其次需滿足線性矩陣不等式(19)。在參考模型穩定的基礎上，式(19)中的Pε應該很容易求得。最后在保證以上兩個基本條件的前提下，可以通過選取不同的參考輸入r(t)和參考模型的矩陣參數，以達到優化跟蹤系統的動態性能的目的。例如，可以通過增加矩陣Am特征根的數值，提高閉環系統的響應速度。

3 仿真驗證

本部分將設計一種自適應控制器，使得即使模糊奇異攝動模型的規則后件參數未知，閉環系統仍然能夠跟蹤穩定參考模型的狀態。假設該模糊奇異攝動模型由兩條規則建立，其規則如下所述。

Rl:如果x1(t)是，則

這里

則可得

假設隸屬函數為

穩態參考模型的參數為

假設 ε =0.11，求解式(19)得

這里參數 A1，A2，B1，B2未知，需要按照式(12)和式(21)、式(22)設計控制律和自適應律，仿真結果如圖1～圖5的實線部分所示。為了便于比較，同時假設模糊奇異攝動模型的參數已知，對系統設計魯棒控制器，仿真結果如圖1～圖5點劃線部分所示。

圖1 跟蹤誤差e1(t)Fig.1 Tracking error of e1(t)

圖2 跟蹤誤差e2(t)Fig.2 Tracking error of e2(t)

圖3 快變量z(t)Fig.3 Fast variable of z(t)

圖4 控制量u1(t)Fig.4 Controller of u1(t)

圖5 控制量u2(t)Fig.5 Controller of u2(t)

從圖1～圖5可以看出，與模糊奇異攝動模型規則后件參數已知時采取魯棒控制所得到的仿真結果相比，采用本文提出的方法使得閉環系統的超調量和調節時間都略有增加，原因在于本章提出的方法是基于模型規則后件參數未知情況下提出的，控制器的增益需要通過自適應調整才能達到穩定值。雖然如此，在15 s以后，控制器輸出仍然能夠達到穩定，系統的慢狀態較好地跟蹤了參考模型的狀態，而快狀態能夠保持穩定。

4 結論

本章提出當模糊奇異攝動模型的參數完全未知情形下的自適應跟蹤控制，不需要模糊奇異攝動模型精確已知，控制器的增益值可以在線自適應調整，仿真結果證明了方法的有效性。

［1］ GAJIC Z，LIM M T.Optimal control of singularly perturbed linear systems and applications-high accuracy techniques［M］.New York:Marcel Dekker，Inc，2001.

［2］ CHOW J H，KOKOTOVIC P V.A decomposition of nearoptimum regulators for systems with slow and fast modes［J］.IEEE Trans.on Automatic Control，1976，21(5):701-705.

［3］ ZHANG X Y，JIN H Z，ZHANG H P，et al.Robust sliding mode control for a class of uncertain nonlinear singularly perturbed systems［C］//Proc.of the 41st SICE Annual Conference，2002，4:2616-2621.

［4］ LIU H P，SUN F C.Survey of singularly perturbed systems:Theory and application［J］.Control Theory and Applications，2003，20(1):1-7.

［5］ SPOONER J T，PASSINO K M.Stable adaptive controls using fuzzy systems and neural networks［J］.IEEE Transaction on Fuzzy System，1996，4(3):339-359.

［6］ TANAKA K，WANG H O.Fuzzy control systems design and analysis:A linear matrix in equality approach［M］.New York:Wiley-Interscience Publication，John wiley ＆Sons，Inc，2001.

［7］ LIU H P，SUN F C.Controller design and stability analysis for fuzzy singularly perturbed systems［J］.Acta Automatic Sinica，2003，29(4):494-500.

［8］ LIU H P，SUN F C.H2state feedback control for fuzzy singularly perturbed systems［C］//Proc.of the 42nd IEEE conference on decision and control，Maul，Hawali USA，2003:5239-5243.

［9］ LIU H P，SUN F C.Simultaneous stabilization for singularly perturbed systems via linear matrix inequalities［J］.Acta Automatic Sinica，2004，30(1):1-7.

［10］ LI Li，SUN Fuchun.An adaptive tracking controller design for non-linear singularly perturbed systems using fuzzy singularly perturbed model［J］.IMA Journal of Mathematical Control and Information，2009，26(4):395-415.

［11］ LI Li，SUN Fuchun.A reference model based adaptive fuzzy controller for nonlinear dynamic systems［C］//FSKD，2009，4:37-41.

［12］ 李莉，孫富春.自適應模糊奇異攝動控制在航天器中的應用［J］.電光與控制，2009，16(10):62-65.