具有限時滯種群發展方程的穩定性區域判定

王 健，岳錫亭，王 雪

（1.長春工業大學 基礎科學學院，吉林 長春 130012；2.吉林農業大學發展學院 基礎教研室，吉林 長春 130600）

0 引 言

對于具有有限時滯的種群發展方程

分別在（τ，D）平面，（τ，r）平面以及（r，D）平面來討論平衡解的穩定性以及穩定區域劃分。

1 穩定性區域劃分

對于方程式（1），可知其平衡點為N＊＝k，作代換＝N＊－k，代入方程式（1），并為方便記，仍用N來表示，有

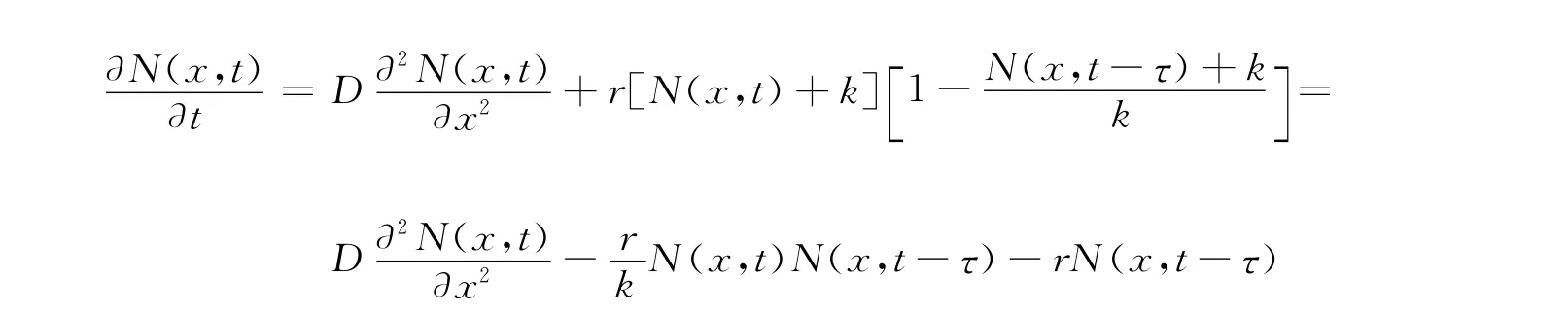
其線性部分為：

易見式（2）有特征函數eλtcosnx，由此得特征方程［1］：

令λ＝ωki，代入式（2），分離實部和虛部，可得方程組：

再由式（4）的第二個方程可知ζk只能在第二象限。

2 考慮3個平面穩定性區域的劃分

在n＝1的情況下，考慮3個平面穩定性區域的劃分。

2.1 在（τ，D）平面的穩定性區域劃分［2］在方程

可見h（ζk）為單調遞增的函數［3］。

在k＝0時，由式（4）第2個方程h（ζ0）＝0，可得：

由式（4）第1個方程g（ζ0）＝0，可得：

在k≠0的一般情況下，易知：

可見D對τ為增函數。

穩定性的劃分：當τ＝0時，λ＝－D－r＜0，在第一條存在純虛根的曲線C0的左側所有根都有負實部［4］，在Ck上時，此時對λ＋D＋re－λτ＝0兩邊對τ求導，得：

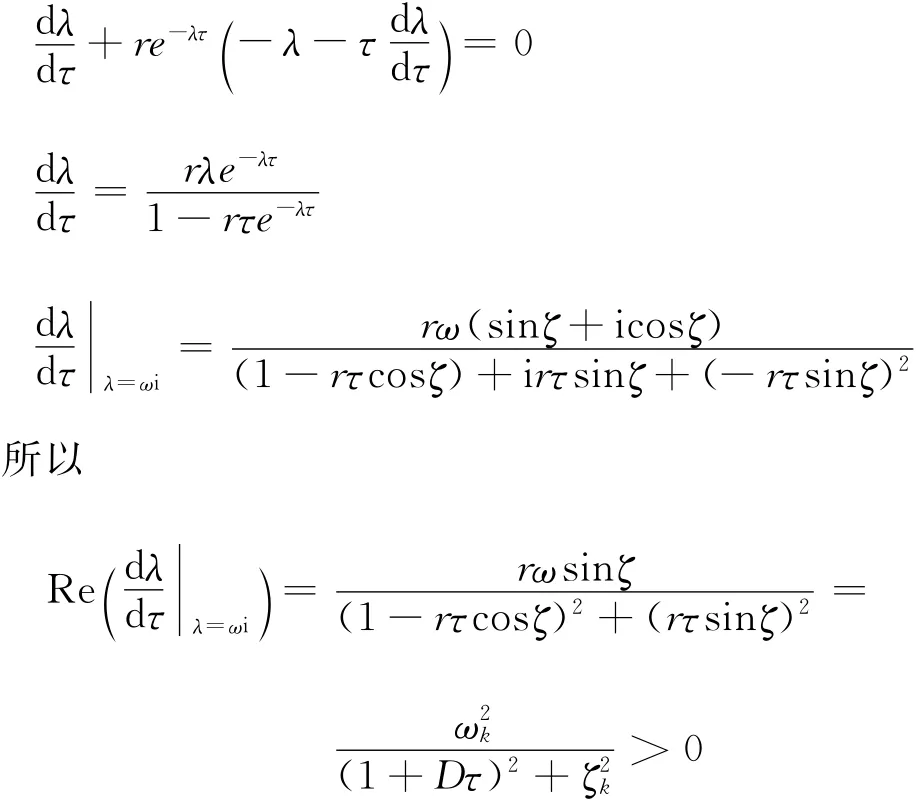
可知，Ck上的純虛根±ωi在C0左側化為負實部的根，右側化為正實部的根，可以證明C0上其余根都有嚴格的負實部［3］。

若假設C0上的某點（τ1，D1）處的特征根為σ＋ω0i（σ＞0），根據根與參數的連續相依性和孤立性，對充分小的正數ε＞0，在（τ1－ε，D1）處這個根的實部仍大于零，但與（τ1－ε，D1）位于C0左側，而C0左側均化為負實部的根矛盾［6］。所以，C0上除一對純虛根外，其余根均具有嚴格的負實部。平衡解在（τ，D）平面的穩定區域如圖1所示。

圖1 （τ，D）平面的劃分

2.2 在（τ，r）平面的穩定性區域劃分

在k＝0時，由式（4）第1個方程g（ζ0）＝0，可得：

由式（4）第2個方程h（ζ0）＝0，可得：

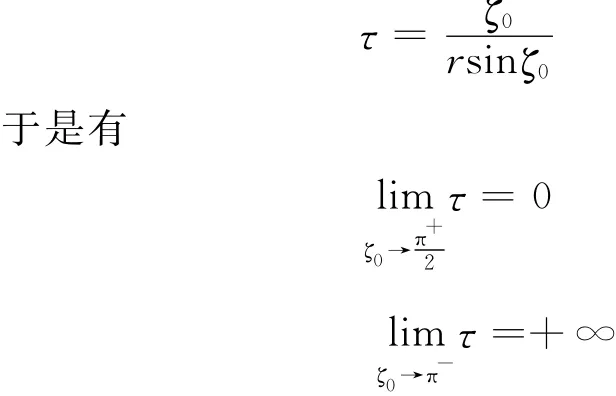
在k≠0的一般情況下，易知：

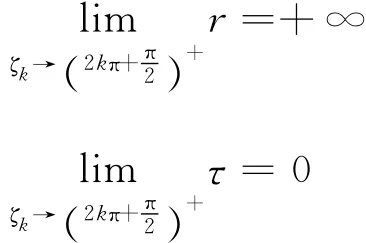
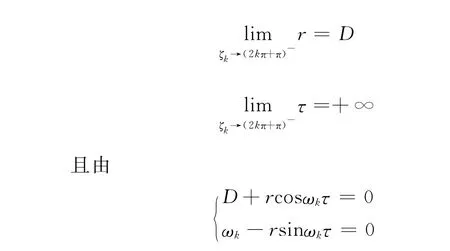
式中對τ求導（D是常數）得：

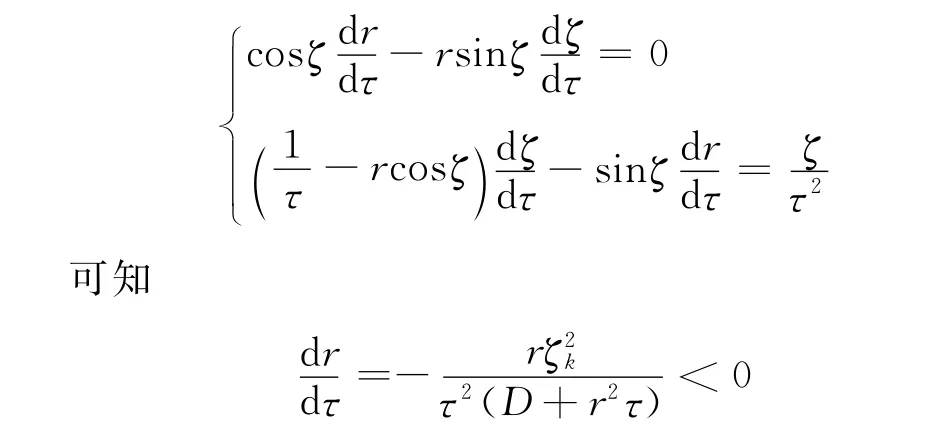
可見，r對τ為減函數。

又由于

可知C0左側為穩定性區域［7］，平衡解在（τ，r）平面的穩定區域如圖2所示。

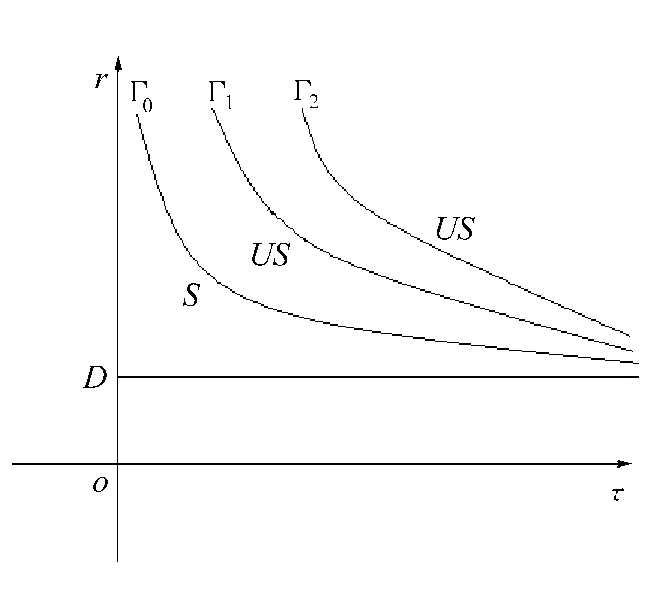
圖2 （τ，r）平面的劃分

2.3 在（r，D）平面的穩定性區域劃分［8］

當k＝0時，由式（4）第2個方程h（ζ0）＝0，可得：

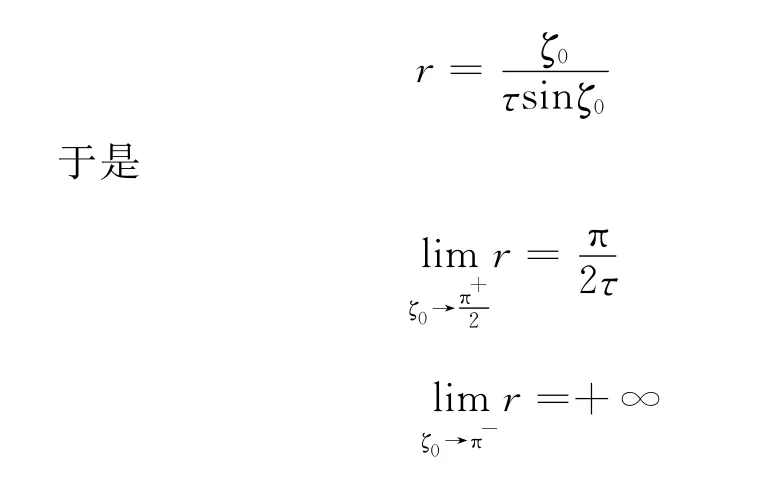
由式（4）第1個方程g（ζ0）＝0，可得：

再由λ＋D＋re－λτ＝0，兩端同時對r求導，可得：

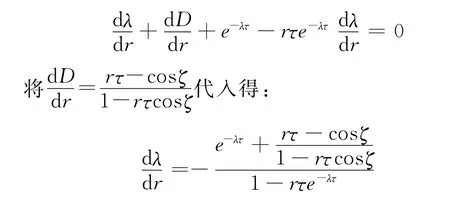
則

可知C0左側為不穩定性區域，右側為穩定區域。平衡解（r，D）在平面的穩定區域如圖3所示。

圖3 （r，D）平面的劃分

［1］岳錫亭.一類二階時滯神經網絡系統穩定區域的劃分及Hopf分支分析［J］.黑龍江大學學報：自然科學版，2006（4）：236－240.

［2］Kreith，G Ladas.Allowable delays for positive diffusion processes［J］.Hiroshima Math.，1985，15：437－443.

［3］Lin P B.Kahn.Phase and amplitude in delay－diffusion population models［J］.J.Math.Biol.，1982，13：383－393.

［4］Luckbaus.Global boundedness for a delay differential equation［J］.Trans Amer.Math.Soc.，1986，294：767－774.

［5］A Schiaffino.On a diffusion volterra equation［J］.Nonlin.Anal.，1979，3：595－600.

［6］Redlinger.On Volterra’s population equation with diffusion［J］.SIAMJ.Math.Anal.，1985，36：135－142.

［7］Jiaqi Pan.Parameter analysis of a chemostat equation with delay［J］.Funkcialaj Ekvacioj.，1998，41：347－361.

［8］張萍，岳錫亭.時滯振動系統的穩定性區域劃分及周期運動分析［J］.長春工業大學學報：自然科學版，2010，31（2）：138－142.

［9］Laron R M，Bojadziev G N.Non－liner differential equations with damping and large time delay［J］.Journal of the Institute of Mathematics and its Applications，1976，17：3－35.