B－不變凸函數的新性質

李 婷，劉凌晨

（山西大學商務學院 理學系，山西 太原 030031）

0 引 言

1981年，Hanson在文獻［1］中引入了凸函數的概念；文獻［2－3］仿照將凸函數推廣為擬凸函數和偽凸函數的方式，對不變凸性做了推廣，給出了擬不變凸性和偽不變凸性的概念；1988年，T.Weir和B.Mond及T.Weir和V.Jeyakumar分別在文獻［3］和文獻［4］中引入了不變凸集和預不變凸函數的定義；1991年，作為對凸函數的推廣，C.R.Bector和C.B.Singh在文獻［5］引入了B－凸函數的定義；1993年，Bector，Suneja和Lalitha在文獻［6］中推廣了B－凸函數、偽B－凸函數和B－凸函數，并分別得到B－不變凸函數、偽B－不變凸函數和擬B－不變凸函數。

定義1［2］設S?Rn關于η：Rn×Rn→Rn是不變凸集，b（x，y）：S×S→R＋，設f（x）是定義在集合S上的可微實值函數，稱f（x）在y∈S是關于η（x，y）的B－不變凸函數，若

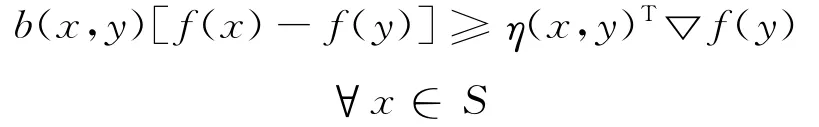
如果f（x）在每一點y∈S關于η（x，y）是B－不變凸的，則稱函數f（x）在S上關于η（x，y）的B－不變凸函數。

定義2［2］設S?Rn關于η：Rn×Rn→Rn是不變凸集，b（x，y）：S×S→R＋，設f（x）是定義在集合S上的可微實值函數，稱f（x）在y∈S是關于η（x，y）的擬B－不變凸函數，若

如果f（x）在每一點y∈S關于η（x，y）是擬B－不變凸的，則稱函數f（x）在S上關于η（x，y）的擬B－不變凸函數。

1 B－不變凸函數的一個性質

引理1［3］（封閉性） S?Rn是開集，f，g是定義在S 上的可微實值函數，f（x）≥0，g（x）＞0，x0∈S，假設f（x），－g（x）在x0點是關于η（x，x0），b（x，x0）的B－不變凸函數，則在x0點是關于的B－不變凸函數。

證明：?x∈S，有

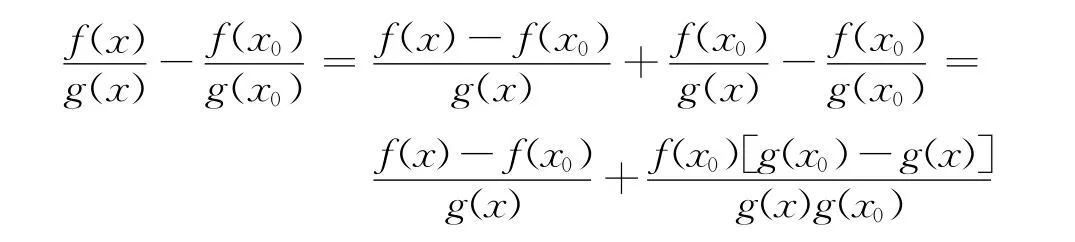
由于f（x），－g（x）在x0點關于η（x，x0），b（x，x0）的B－不變凸的，并且f（x）≥0，g（x）＞0，有

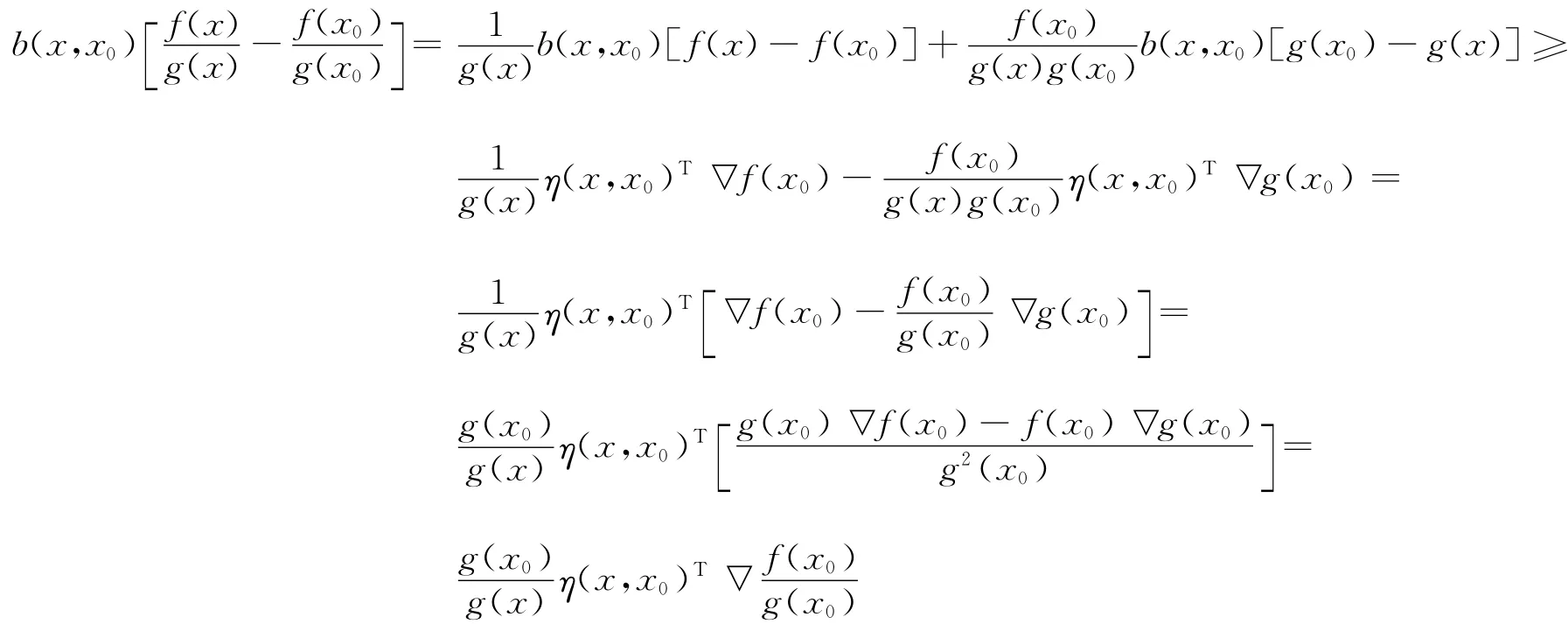
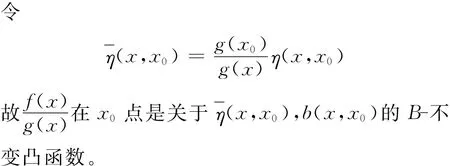
定理1 S?Rn是開集，f，g是定義在S上的可微實值函數，f（x）≥0，g（x）＞0，x0∈S，假設f（x），－g（x）在x0點是關于η（x，x0），b（x，x0）的B－不變凸函數，則在x0點是關于（x，x0）＝g2（x0）η（x，x0），b（x，x0）的擬 B－不變凸函數。

證明：?x∈S，有

g（x0）［f（x）－f（x0）］＋f（x0）［g（x0）－g（x）］≤0上面不等式兩端同時乘以b（x，x0）得：

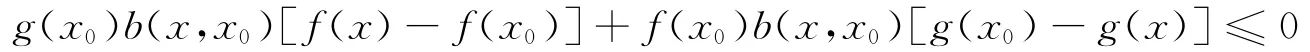
由f（x），－g（x）在x0點關于η（x，x0），b（x，x0）是B－不變凸的，我們有

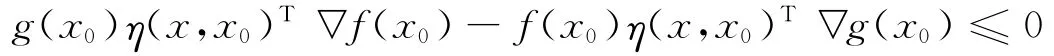
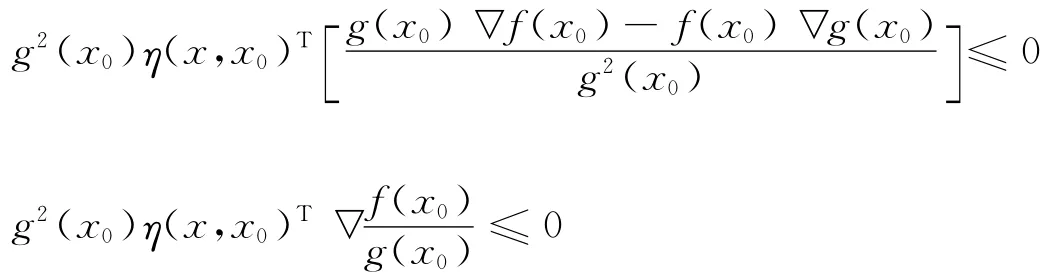
上面不等式兩端同時乘以b（x，x0），得：

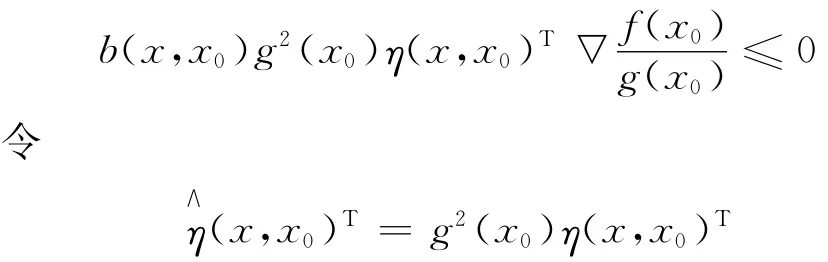
可得結論。

［1］ M A Hanson.On sufficiency of the Kuhn－tucker conditions［J］.J.Math.Anal.Appl.，1981，80（2）：544－550.

［2］B D Craven，B M Glover.Invex functions and duality［J］.J.Austral.Math.Soc.，（Ser.A），1985，39：1－20.

［3］T Weir，B Mond.Preinvex functions in multipleobjective optimization［J］.J.Math.Anal.Appl.，1988，136（1）：29－38.

［4］T Weir，V Jeyakumar.A class of nonconvex functions and mathematical programming［J］.Bull.Austral.Math.Soc.，1988，38：177－189.

［5］C R Bector，C Singh.B－vex functions［J］.J.Opti.Theo.Appl.，1991，71：237－253.

［6］C R Bector，S K Suneja，C S Lalitha.Generalized B－vex functions and generalized B－vex programming［J］.J.Opti.Theo.Appl.，1993，76：561－576.

［7］趙克全，黃應全.B－不變凸分式規劃的最優性條件及對偶定理［J］.湖北民族學院學報，2004，22（3）：19－21.

［8］林銼云，董加禮.多目標規劃的方法與理論［M］.長春：吉林教育出版社，1992.