大型風力機復合材料葉片動態特性及氣彈穩定性分析

劉 偉，尹家聰，陳 璞，蘇先樾

(北京大學力學與空天技術系湍流與復雜系統國家重點實驗室，北京 100871)

0 引言

隨著現代風力發電技術的日益成熟，全球風電產業近年來發展勢頭良好，大功率、兆瓦級風力發電機大量投入使用。與此同時，風力發電機的空氣動力學特性及其結構優化設計也逐漸受到研究人員的廣泛關注。葉片作為風力發電機的核心部件，其良好的結構特性是整個機組實現長期安全高效運行的前提，因此風機葉片的結構設計與分析是風機設計的重要環節。風機葉片一般展向長、弦向短，因而當前多數風機葉片的結構分析及優化設計研究均采用近似梁模型進行［1-2］。然而，由于目前大型風機的葉片普遍采用各種具有輕質高強特點的纖維增強復合材料制成，從整體上葉片可以看成是一種復雜薄壁結構。此時采用近似梁模型進行葉片結構分析，其結果可能無法滿足精度要求［3］。此外，近似梁模型雖然能夠在一定程度上反映葉片的整體性能，卻無法揭示葉片的細節結構特性，如葉片在氣動載荷下可能的局部屈曲［4］。

本文探索大型復合材料葉片三維殼模型的快速參數化建模技術，以及利用三維殼模型進行的葉片結構動態特性分析及靜氣彈穩定性分析。針對某初步設計的1.5MW風機葉片，首先采用參數化建模技術建立風力機復合材料葉片三維殼模型，并在此基礎上對葉片的固有動力學特性進行分析，其中旋轉工況下的分析考慮了離心力導致的應力剛化及旋轉軟化等附加效應的影響。然后，通過編制插值程序解決葉片氣動力計算網格與結構計算網格不匹配問題，將CFD計算所得葉片表面分布壓力導算到葉片結構計算有限元模型上，并以此為載荷對葉片進行靜氣彈穩定性分析，預測葉片發生局部屈曲的可能性及其發生的位置。

1 參數化建模

風機葉片的外形與內部結構較為復雜，一般由前緣、后緣、梁帽、腹板等不同區域組成的，不同的區域具有不同的復合材料鋪層，因此在結構分析的三維殼模型建模過程中必須把葉片殼體按照鋪層方式的不同分割為不同的材料面，以便對其賦予各自的復合材料參數。

本文利用計算幾何方法，編制Matlab參數化建模程序。程序通過讀取葉片控制截面翼型數據、沿展向分布的弦長、扭轉角數據以及葉片各部分的復合材料鋪層等各種幾何、材料信息，自動輸出通用有限元軟件ANSYS能夠讀取的APDL命令流文件，由此快速建立葉片的三維幾何模型。

以某初步設計的1.5MW風機葉片作為例，該風機葉片長度為40.5m，額定轉速為17.2r/min。葉片典型翼型截面如圖1所示。根據復合材料鋪層方式的不同，上下表面各被分為5段:后緣加強層、后緣夾芯層、梁帽、前緣夾芯層以及前緣加強層。該葉片有前、后兩個腹板。

采用本文所發展的參數化建模技術建立該風機的三維殼模型，如圖2所示。由于各部分的鋪層差異，葉片的外殼和前后腹板共被分作357個材料面。

在參數化建模的基礎上，選擇合適的單元尺寸，采用適合于復合材料層合板殼結構線性與非線性分析的八結點殼單元SHELL281對葉片的幾何模型進行離散，生成的有限元模型如圖3所示。最后，約束葉片根部圓周上所有結點自由度以模擬法蘭盤對葉片的固定約束。

圖1 某1.5MW風機葉片的典型截面示意圖Fig.1 Schematic of a typical cross-section of the wind turbine blade

圖2 某初步設計的1.5MW風機葉片三維模型Fig.2 Three-dimensional geometric model of the wind turbine blade

圖3 某初步設計的1.5MW風機葉片有限元模型Fig.3 Finite element shell model of the wind turbine blade

2 模態分析

風機正常運行過程中，葉片處于旋轉狀態，其在旋轉坐標系中的振動方程為:

式中M，K分別為葉片的質量和剛度矩陣。Kg和Kc分別是離心力導致的剛度矩陣改變，與轉速的平方成正比。離心力的這兩種作用在有限元分析中分別被稱為“應力剛化效應”和“旋轉軟化效應”。G是由科氏力引起的，與轉速成正比。計算表明:由于大型水平軸風力機轉速一般較低，G對葉片固有頻率的影響十分微弱，可以忽略。

利用上述參數化建模方法建立的1.5MW風機葉片有限元殼模型，在停機工況和17.2r/min額定轉速工況下分別對葉片進行模態分析，結果如表1所示。從表1可知，由于該風機的額定轉速僅為17.2r/min，離心力引起的應力剛化和旋轉軟化效應對葉片各階模態頻率的影響很小。

表1 某初步設計的1.5MW風機葉片前15階模態的頻率Table1 The lowest 15 natural frequencies of the wind turbine blade

值得注意的是，葉片的前15階模態中，共有9階為腹板根部的局部模態，且最低在第6階就出現了局部模態。這是由于初步設計中，兩腹板在靠近根部區域的鋪層設置過薄，彎曲剛度過低，從而導致此區域腹板在相對較低的頻段內即出現局部彎曲模態。根據上述分析，建議在葉片的后續設計中增加腹板在這一區域的厚度。此例說明:采用三維殼模型進行葉片結構分析有利于揭示葉片的薄弱部位，而采用梁模型則無法揭示葉片的這些細節特性。

3 靜氣彈穩定性分析

本文中考慮的靜氣彈穩定性分析主要是指定常氣動載荷下的葉片結構屈曲分析。如前所述，大型風機復合材料葉片結構從整體上看近于復雜薄殼結構，因此在其結構設計中已由過去主要考慮疲勞破壞發展到目前必須同時考慮結構穩定性問題。關于風機葉片的屈曲，國內外已有部分工作［5-6］。然而，這些工作都是采用近似梁模型完成的。盡管也有個別研究人員曾用殼模型進行葉片屈曲分析［7］，但是，其采用的葉片表面壓力分布僅僅是一種人為假定的三角壓力分布。隨著CFD技術和計算機軟硬件的不斷發展，CFD技術被越來越多地應用于風機氣動性能及載荷特性的預測［8］。與動量葉素理論等簡化理論相比，CFD技術能夠提供更多的細節，如更真實的葉片表面壓力分布。本文將CFD計算所得葉片表面分布壓力導算到葉片結構計算有限元模型上，并以此作為載荷進行葉片屈曲分析。

3.1 分布壓力的導算

CFD計算提供的葉片表面分布壓力結果文件中提供的信息一般是CFD計算中所使用的葉片表面網格結點的坐標及其壓力值。CFD計算時對葉片表面進行離散所需的網格數一般比結構計算所需有限元網格數目要大得多。此外CFD計算過程中建立葉片的幾何模型時一般只關注葉片表面的形狀，因此只需要建立葉片表面的幾何模型，與此相對，結構建模需要考慮葉片表面各區域不同的復合材料鋪層以及腹板等內部結構。由于在建模上有上述不同的側重點，風機葉片CFD計算和結構計算一般無法采用同一套網格進行。我們的解決方案是:分別建立各自的網格，首先進行CFD計算，完成后輸出葉片表面網格上的分布壓力，然后將流體網格上的壓力導算到結構有限元模型上，最后進行結構計算。本文通過編制插值程序以實現上述壓力導算過程，其流程如圖4所示。

圖4 分布壓力導算過程示意圖Fig.4 A flowchart of the pressure mapping procedure

針對本文所考慮的算例，采用六個典型風速下的分布壓力進行屈曲分析，六個風速分別為6m/s、10.5m/s、13m/s、16m/s、19m/s 和 25m/s。采用上述壓力導算程序分別將這個六個風速下CFD計算所得的葉片表面分布壓力施加到葉片三維有限元殼模型上。圖5以16m/s為例給出了該風速下導算到葉片結構模型上的分布壓力圖。

圖5 葉片有限元模型上施加的分布壓力(風速:16m/s)Fig.5 Pressure applied on the finite element model of the blade(wind speed:16m/s)

3.2 屈曲分析

采用前文中建立的復合材料殼模型，將上述六個風速下的分布壓力導算到有限元模型后進行屈曲分析，分析中仍然考慮了離心力引起的應力剛化和旋轉軟化效應。計算所得上述六個風速下葉片的前四階屈曲載荷因子列于表2中。

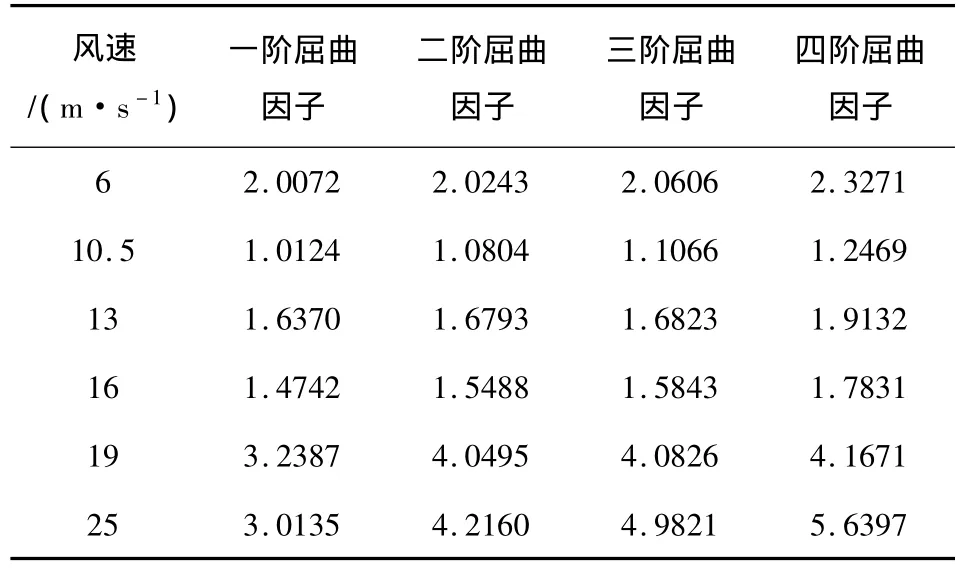
表2 某初步設計的1.5MW風機葉片屈曲載荷因子Table2 Load factors of first 4 buckling modes

從表2中可以看出，所分析風速下葉片屈曲載荷因子都大于1，因此葉片在所考慮的六個典型風速下不會發生屈曲。由于本風機采用變槳距控制方式，當風速增加時，葉片槳距角增大，葉片表面壓力并不隨著風速單調增加，因此各階屈曲載荷因子也并不隨著風速單調減小。從屈曲載荷因子來看，在所考慮的六個風速中10.5m/s和16m/s對應的等效載荷較大。

仔細檢查葉片在這六個風速下可能的屈曲模態發現，這些模態都是發生于腹板根部的局部屈曲。圖6以16m/s風速為例給出了該風速下葉片的前四階屈曲模態，由于是腹板根部的局部屈曲，為了方便觀察，圖中只顯示了腹板。六個典型風速下的屈曲模態都是腹板根部的局部屈曲，反映了腹板根部設計較為薄弱，模態分析中腹板根部局部振型過早出現也揭示了這個問題。

4 結論

本文發展了大型復合材料風機葉片三維殼模型的參數化建模技術以及基于殼模型的葉片模態分析技術與靜氣彈穩定性分析技術。

利用參數化建模技術，通過給定葉片外形、內部構造及復合材料鋪層信息，可快速建立細致的有限元三維殼模型。采用三維殼模型進行葉片結構動態分析及靜氣彈穩定性分析的結果表明，近似梁模型無法揭示風機葉片結構的細節特性，采用殼模型進行分析有利于識別葉片結構的薄弱部位。

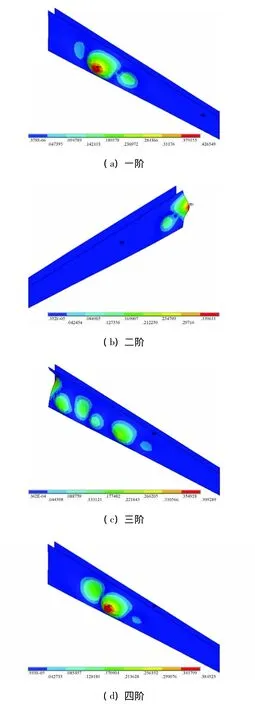
圖6 葉片前四屆屈曲模態(風速:16m/s)Fig.6 Buckling shapes of first 4 buckling modes(Wind speed:16m/s)

［1］劉雄，李鋼強，李嚴，等.水平軸風力機葉片動態響應分析［J］.機械工程學報，2010，46(12):128-141.

［2］廖猜猜，王建禮，石可重，等.風力機葉片截面剛度優化設計［J］.工程熱物理學報，2010，31(7):1127-1130.

［3］YIN J C，XIE Y，CHEN P.Modal analysis comparison of beam and shell models for composite blades［A］.Asia-Pacific Power and Energy Engineering Conference［C］.Wuhan，China，2009.

［4］LIU W，MA Y L，SU X Y，et al.Buckling analysis of wind turbine blade using pressure distributions obtained from CFD［A］.Asia-Pacific Power and Energy Engineering Conference［C］.Wuhan，China，2009.

［5］BIR G S，MIGLIORE P.Preliminary structural design of composite blades for two and three blade rotors［R］.NREL/TP-500-31486.Golden，CO:National Renewable Energy Laboratory，2004.

［6］HERMANN T M，MAMARTHUPATTI D，LOCKE J E.Postbuckling analysis of a wind turbine blade substructure［J］.Journal of Solar Energy Engineering-Transactions of the Asme，2005，127(4):544-552.

［7］MCKITTRICK L R，CAIMS D S，MANDELL J，COMBS D C，RABERN D A，VAN LUCHENE R D.Analysis of a composite blade design for the AOC 15/50 wind turbine using a finite elementmethod［R］.SAND 2001-1441.Sandia National Laboratories，2001.

［8］LEISHMAN J G，GLENN L M.Challenges in modeling the unsteady aerodynamics of wind turbines［J］.Wind Energy，2002，5(2):85-132.