基于伴隨方程方法的非結構網格自適應技術及應用

李 立，白 文，梁益華

(1.中國航空工業集團公司第六三一研究所，陜西 西安 710068;2.中國航空研究院航空數值模擬技術研究應用中心，北京 100012)

0 引言

隨著技術進步，計算流體力學(CFD)已成為飛行器氣動力設計的例行工具和日常應用手段。但計算網格生成一直是制約CFD技術發展的一個瓶頸。通常對于復雜的計算問題，整個數據準備的70%以上工作量都被用于生成計算網格。近年來，非結構網格(尤其是非結構/結構混合網格)因其對復雜幾何外形的適應能力和良好的自動生成能力，在復雜外形流場模擬中的應用受到越來越多的重視［1］。本文圍繞非結構自適應網格生成技術開展研究，其目標是改進非結構網格技術在復雜流動物理流場的模擬能力。

網格自適應技術的核心是構造各種自適應探測器。不同的探測器對應不同的網格自適應方法［2］。目前，主要有兩類構造自適應探測器的典型方法。一類是基于流動特征的傳統方法，如采用流場變量的差量、梯度等作為探測器。該類方法普遍認為［3］，流場中梯度變化大的位置對流場計算精度的影響越大。主流商業軟件CFX、Fluent等所采用的策略都屬此類。一類是基于敏感性分析的新興方法，如本文研究的基于流場伴隨方程的網格自適應探測器。與傳統方法相比，基于伴隨方程的網格自適應方法是一種基于全局后驗誤差估計的方法，直接建立了流場誤差與目標輸出(如升力、阻力和力矩等)誤差的關聯關系，可有效避免因錯誤判斷加密區域導致的網格過度加密［3］，提高計算效率和目標輸出的計算精度［4-5］，從而有效削減氣動數值模擬對計算網格的敏感性。

本文對基于伴隨方程的網格自適應技術的基本原理進行了研究，構造了基于流場伴隨方程的網格自適應探測器(伴隨自適應探測器)，利用局部加密網格的辦法，建立并實現了基于Euler方程的無粘伴隨自適應能力。對于粘性流動問題，提出首先應用無粘計算和伴隨自適應從基準網格自動生成具有較好網格分辨率的非結構自適應網格，然后采用層推進法自動生成粘性網格的求解策略。通過對具體算例開展的數值試驗，表明本文建立的方法是有效的。

1 數值方法

1.1 流場主控制方程的計算方法

出發方程為Euler方程或雷諾平均的N-S方程，應用格點格式的有限體積方法離散，控制體采用對偶方法生成，空間離散采用標準的Jameson中心差分格式，時間推進采用三階顯式Runge-Kutta格式。另外，在實際計算中，均采用三重多重網格W循環的聚合多重網格算法進行計算加速。對于粘性計算，湍流模型采用Menter SST k-ω 模型。

1.2 流場伴隨方程的計算方法

流場伴隨方程的定義式如下［4-5］:

其中，λ即伴隨變量，R為流場控制方程殘差，Q為流場解變量，f為目標輸出函數(如升力、阻力、力矩等)。顯然，當流場解已知，伴隨變量就可以通過求解式(1)得到。為了解的穩定性和計算過程的魯棒性，本文采用求解流場主控制方程的類似辦法，通過在伴隨方程中添加虛擬時間項進行時間推進求解［7］:

這里，Rλ(λ)為伴隨方程的殘差，

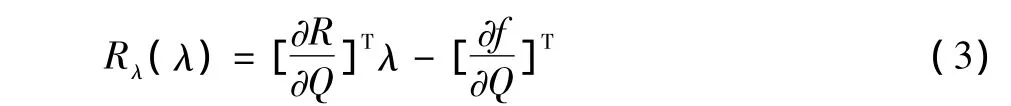
實際求解時，對式(2)，與流場主控制方程一樣，采用格點格式的有限體積方法離散，空間離散采用標準Jameson中心差分格式，時間推進采用三階Runge-Kutta顯式格式，并采用多重網格加速。

1.3 伴隨自適應探測器

通過伴隨變量可直接建立目標輸出殘差與流場殘差之間的關系［4］:

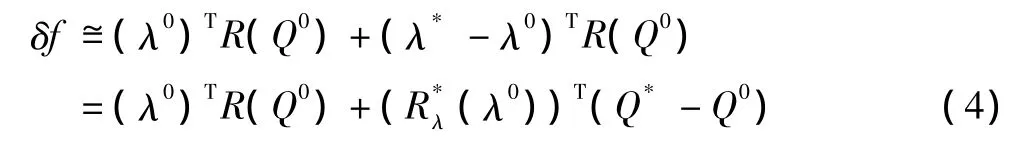
式中，(λ0，Q0)表示初始網格上的伴隨解和流場解;(λ*，Q*)表示理論解或非常密網格上的解，一般無法直接給出;R(Q0)表示粗網格上流場控制方程的殘差;表示在非常密網格上伴隨方程的殘差。

由式(4)不難分析，影響目標輸出的誤差項可分為兩部分。一部分是可利用現有網格直接計算的絕對誤差項(λ0)TR(Q0)，而剩下的一部分是需在更密網格上計算才能得到的修正誤差項。這表明，如對修正誤差項加以估計，就可判斷計算網格中哪些位置對目標輸出有更大的影響，進而可用于建立新型的網格自適應探測器，即伴隨自適應探測器。本文中，伴隨自適應探測器定義如下:

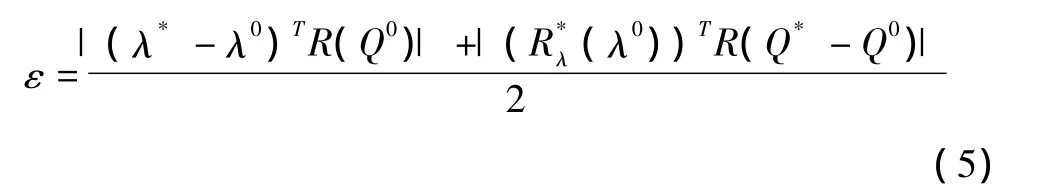
通過估計或判斷該值大小就可標記出流場中哪些位置的網格最需要加密。

1.4 自適應網格生成策略

自適應網格生成的一般性策略和方法在文獻［2，8］有較詳細的介紹。本文采用局部加密網格的辦法(又稱h-方法)來進行自適應網格生成。h-方法通過細劃網格單元來實現自適應網格生成，通常分為點插入、粗網格細分和網格重構等三類方法。本文采用的方法屬于粗網格細分法。該方法依賴于自適應探測器所標記的邊。根據邊的標記情況，對于四面體，共有三種細分網格的模式，分別為二分模式、四分模式和八分模式。本文自適應網格生成策略如下:首先通過伴隨自適應探測器對網格單元進行標記，然后根據網格單元的標記情況，采用二分模式進行各向同性加密。對四面體單元，其方法是連接四面體最長邊的中點和該邊所對的2個點，從而將四面體分成2個子四面體。為了利用式(5)定義的自適應探測器對網格單元或邊進行標記，公式中的理論解或非常密網格上的解首先必須用從原始粗網格的解(λ0，Q0)往一個全局加密網格上插值得到的解(λh，Qh)代替。這里，全局加密網格采用八分模式進行網格劃分來自動生成。為了簡單，文中采用分段線性插值來計算全局加密網格的解。通過循環掃描粗網格的每個單元所包含的全局加密網格的網格點并由式(5)來估計當地實際的修正誤差:

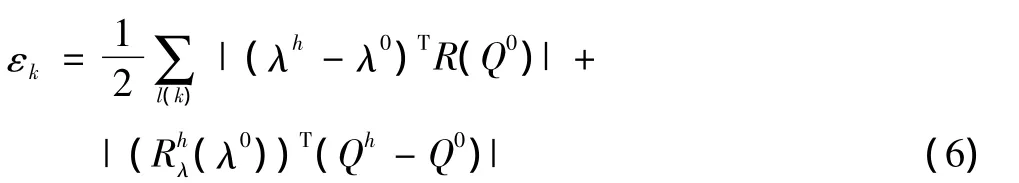
自適應準則定義如下:用戶給定全局誤差閥值ε，按照誤差等分布的原則，判斷當地誤差與平均全局誤差的比值η=N·εk/ε是否大于1，如該條件成立，則對所在的單元進行標記。這里，N表示現有粗網格的網格點數。

值得指出，采用二分模式對四面體網格進行自適應剖分可能會導致自適應后的網格包含懸掛點或非四面體單元，并且還有可能使自適應網格的網格質量比較差，因此采取措施消除懸掛點和對網格進行光順非常必要［9］。推薦將自適應后的網格導入通用網格生成軟件進行必要的處理。

1.5 粘性網格生成

為了捕捉邊界層內的粘性流動，必須在沿物面法向的一定厚度內生成各向異性網格，即需將原始的純四面體非結構網格轉換成混合網格。混合網格中可能包含的網格單元類型有四面體、棱柱、六面體或金字塔單元。有多種方法可以實現從四面體網格自動生成混合網格，本文推薦采用層推進方法［10］。其思路是在物面附近按期望的邊界層厚度通過網格局部重構產生貼體的棱柱單元，而在這一厚度之外的大部分網格單元保持不變，過渡單元采用四面體或金字塔單元填充。

2 程序校驗和方法驗證

2.1 RAE2822跨聲速翼型計算

RAE2822跨聲速翼型是一個超臨界翼型，在全世界得到廣泛研究，其試驗結果被用于大量流場解算器的驗證［11］。這里，選取的計算狀態為 Case 9:M∞=0.734，攻角α=2.79°。初始計算網格如圖1(a)所示，共有15852個網格點，31388個三角形網格單元。圖1(b)給出由初始網格得到的馬赫數云圖。可以看到，該初始網格較好地捕捉到流場的激波結構。選用升力系數作為目標輸出函數進行自適應，設定全局誤差閥值為0.1。自適應后的網格如圖1(c)所示，共有20763個網格點，41141個三角形單元。可以看到，伴隨自適應加密的區域主要在翼型的前緣、上表面和激波區，這和主要流動的特征非常匹配，也正是我們希望加密的區域。按伴隨自適應探測器的基本原理，這同時還表明，RAE2822翼型的前緣、上表面和激波區對于準確計算升力有主要貢獻。

2.2 ONERA-M6跨聲速機翼計算

圖1 RAE2822跨聲速翼型的伴隨自適應結果Fig.1 Effect of mesh adaptation for RAE2822 airfoil

圖2 ONERA-M6跨聲速機翼的伴隨自適應結果Fig.2 Effect of mesh adaptation for ONERA-M6 wing

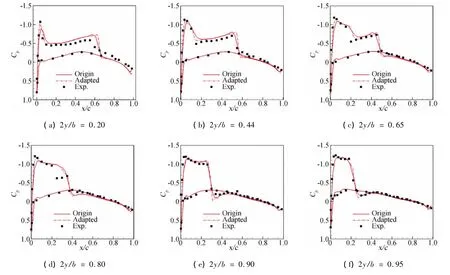
圖3 自適應前后ONERA-M6機翼物面沿展向壓力系數分布的對比Fig.3 Comparison of spanwise pressure coefficient distributions between before and after adaptation with experimental data for ONERA-M6 wing

與RAE2822翼型一樣，ONERA-M6機翼也是一個經典的驗證算例［12］。這里，選取的計算狀態為:M∞=0.84，攻角α=3.06°。初始計算網格為純四面體網格，包含52144個網格點，296517個四面體單元，其中，機翼物面分布的網格點數為5459。圖2(a)給出了初始的機翼物面網格。可以看到，初始的物面網格點在機翼表面分布比較均勻，除在翼尖、機翼前緣位置從幾何保形的角度作了處理外，沒有從流動特征方面作任何特殊考慮。同樣，選用升力系數作為目標輸出函數進行自適應，設定全局誤差閥值為0.1。自適應后的四面體網格共有128386個點，740366個四面體單元，其中機翼物面分布的網格點數為8041。圖2(b)給出自適應后物面網格的示意圖。從自適應的物面網格點分布可以很清晰看到一個呈現λ形的加密區域。這也正好對應本計算狀態下ONERA-M6機翼表面應呈現的激波結構。從圖中可看出，通過自適應，網格點對機翼前后緣也進行了加密。圖2(c)給出由自適應網格得到的ONERA-M6機翼物面馬赫數云圖，計算得到的機翼表面 激波非常清晰。圖3比較了自適應前后計算得到的機翼物面沿展向壓力系數分布。從壓力系數(尤其在靠近翼根的位置)的比較，可以看到，對于ONERA-M6機翼，采用伴隨自適應還可在一定程度上提高計算的精度。

3 復雜流場計算應用

這一節討論伴隨自適應技術在復雜流場計算中的應用。選擇的考核算例是第二屆國際渦流試驗項目(VFE-2)中的尖前緣65°三角翼模型［13］，主要考察伴隨自適應技術在提高基于非結構網格的CFD技術預測大攻角復雜渦流場的能力。VFE-2項目是美國和歐洲在2004年聯合發起的國際合作項目，采用NASA Langley研究中心提供的不同前緣鈍度的三角翼標準模型作為研究對象，旨在確認和評估當前CFD方法在復雜渦流場的預測能力和技術狀態。關于該模型的介紹和具體描述參見文獻［14］。本文選取的計算狀態是:M∞=0.4，攻角α=20.3°。對于粘性計算，基于平均氣動弦長的雷諾數Re=2.0×106。為了減小計算量，實際計算中，采用半翼展模型開展計算研究。

3.1 無粘計算結果

初始網格采用純四面體網格，包含64835個網格點，365681個四面體單元，其中，物面上分布的的網格點為9464個。對于初始計算網格，除了從幾何保形方面考慮對三角翼前后緣適當進行加密控制外，沒有進行任何特殊處理。圖4(a)上半部分給出了三角翼初始的物面網格，可以看到，物面上點的分布幾乎是均勻的。圖4(a)下半部分是由該初始計算網格采用無粘計算得到的物面壓力系數分布云圖，給出了一個很明顯的低壓區。這一低壓區正是三角翼上表面前緣渦掃過的痕跡，說明由初始計算網格可捕捉到渦流場的存在。仍選用升力系數作為目標輸出函數進行伴隨自適應，全局誤差閥值設為0.1。自適應后的四面體網格共有139682個網格點，766948個四面體單元，其中，物面上分布的網格點為13333個。圖4(b)上半部分給出了自適應后的三角翼物面網格示意圖。很明顯，自適應加密的物面網格點主要分布在機翼翼根、機翼前后緣以及計算捕捉到的前緣渦所掃過的區域。圖4(b)下半部分給出了由自適應網格計算得到的物面壓力系數分布云圖。與上圖比較，不難看到，自適應后得到的低壓區更加清晰，這表明捕捉到的前緣渦的強度有所增加。

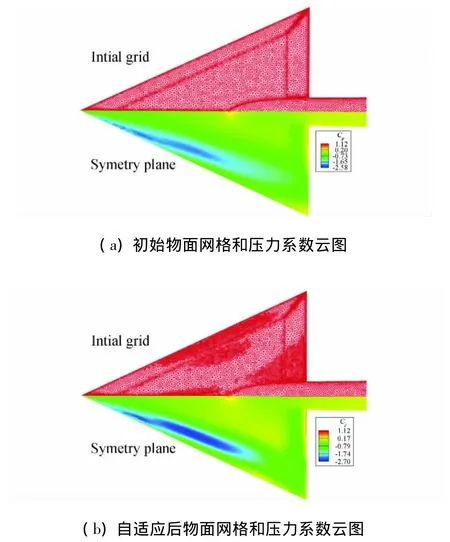
圖4 VFE-2尖前緣65°三角翼模型自適應前后結果的對比Fig.4 Comparison of mesh and pressure coefficient distribution on the wall surface between before and after adaptation for VFE-2 delta wing with sharp leading-edge

圖5通過沿流向方向截取兩個典型站位x-c=0.4及x-c=0.6的空間網格，對比了自適應前后空間網格的變化。可以看到，對于此算例，空間網格主要在靠近機翼上表面的位置(尤其是翼根和主渦的附近)進行加密，而在機翼下表面附近網格幾乎沒有任何加密。并且，在流向方向的不同站位，網格的加密位置和密度隨主渦渦核的位置和強度有所變化，但并不完全集中在渦核周圍。這與基于流動特征的渦自適應或熵自適應方法觀察到的有明顯差別［2］。

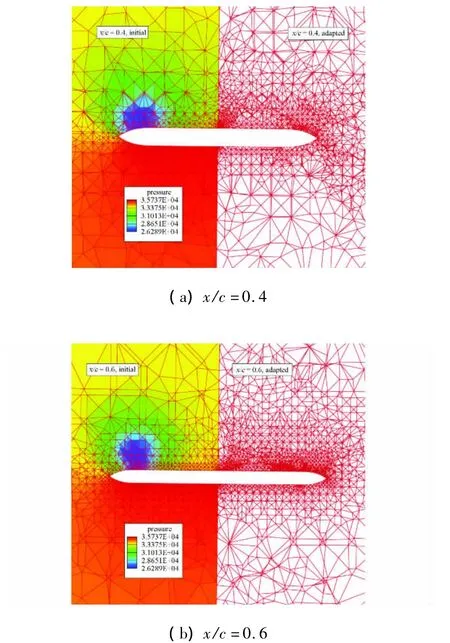
圖5 尖前緣65°三角翼模型自適應前后兩個典型站位的空間網格對比Fig.5 Comparison of mesh resolution in space from two typical sections for VFE-2 delta wing with sharp leading-edge

圖6比較了自適應前后采用無粘計算得到的尖前緣65°三角翼在典型站位的物面壓力系數分布。可以看到，自適應前后，采用無粘計算在預測渦核的位置和主渦吸力峰強度方面都有很大改善，但與試驗相比，整體上偏差都比較大。這也從側面印證了人們長期形成的一個計算經驗，即采用Euler方程進行無粘計算不足以很好地預測三角翼大攻角渦流場這類存在大的分離和以渦流為主導的復雜流場。

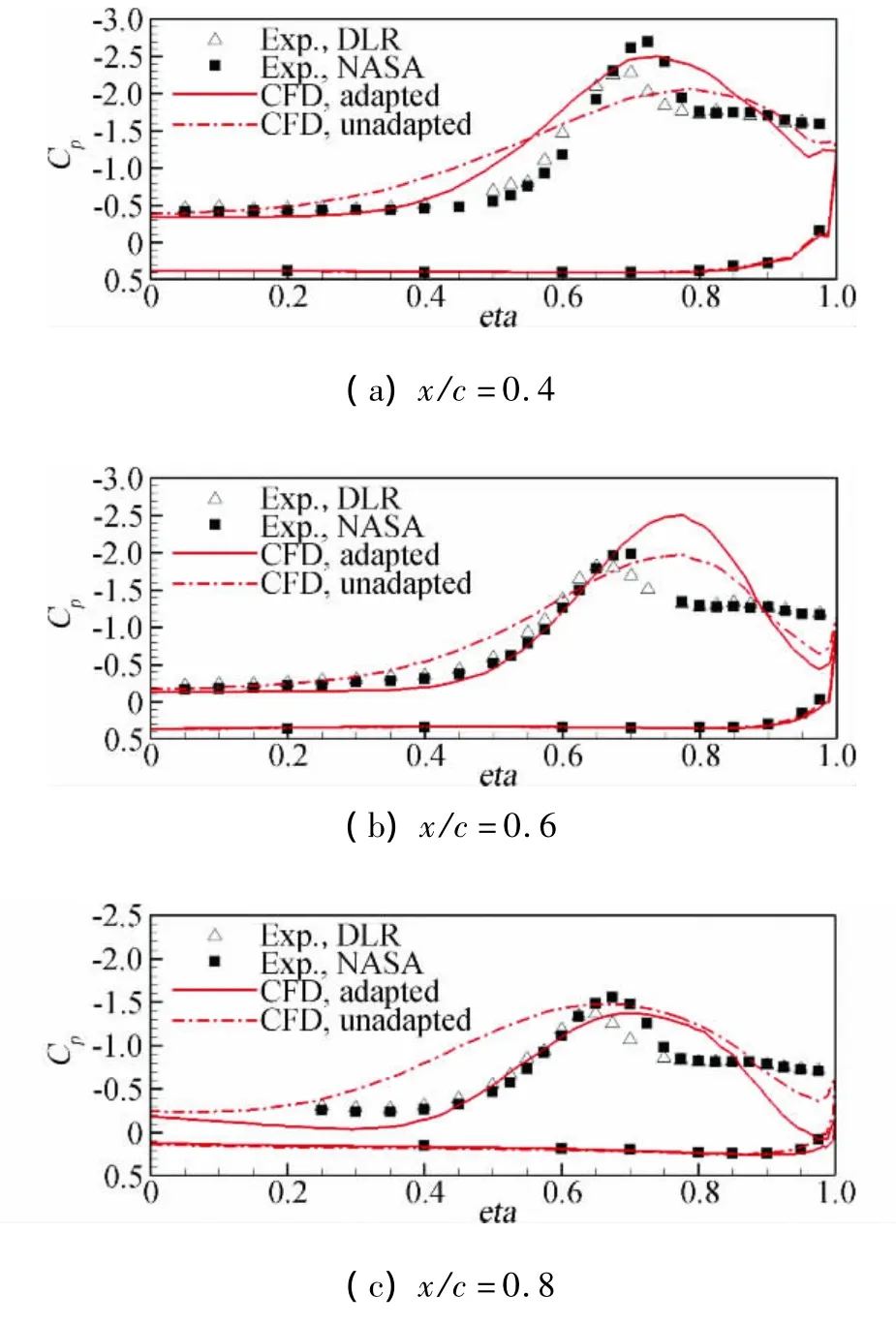
圖6 自適應前后尖前緣65°三角翼模型在典型站位的物面壓力系數分布與試驗值的對比(無粘計算)Fig.6 Comparison of pressure coefficient distributions between before and after adaptation with experimental data for VFE-2 delta wing with sharp leading-edge(in inviscid computation)

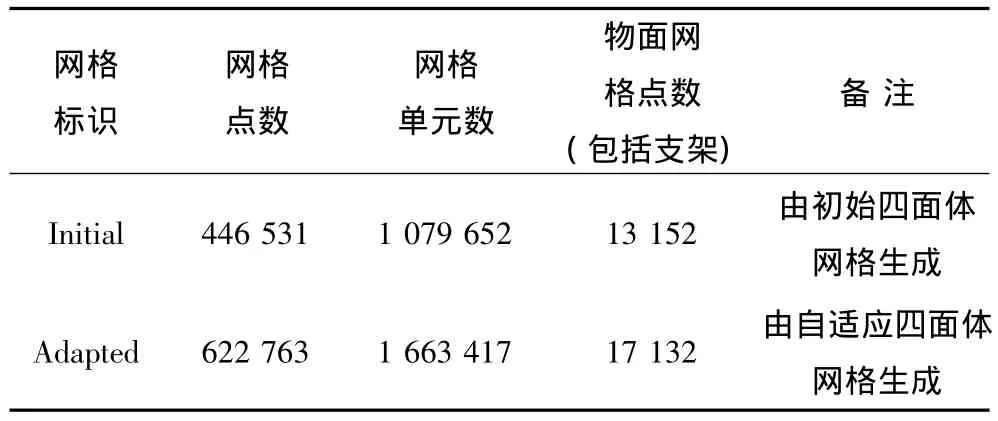
表1 兩套粘性計算網格的網格信息統計Table1 Information for two meshes in viscous computations

3.2 粘性計算結果

在粘性計算中，粘性計算網格分別在初始四面體網格和自適應后的四面體網格基礎上生成。為了保證第一層網格的Y+≈1，邊界層內第一層網格距離物面的距離按0.01進行估計。在實際計算中，取第一層網格的實際間距為5.0×10-6，網格拉伸比為1.2，總的附面層網格層數為30層。兩套網格的詳細信息參見表1。

為了比較計算效果，圖7首先給出利用兩套粘性計算網格得到的物面極限流線和空間流場解的對比。計算中所有參數設置在前后保持一致。從物面極限流線的結果看，由自適應局部加密的粘性網格得到的解不僅觀察到主再附線(說明渦流場存在)，而且還清晰觀察到二次再附線，而由初始粘性網格得到的解僅能觀察到主再附線，二次再附線不明顯。并且，兩者主再附線的位置明顯有差別，由初始粘性網格得到的主再附線更靠近翼尖的位置。這表明，由自適應局部加密的網格得到的主渦位置會明顯沿展向翼根靠近。從空間流場解的結果進行分析，圖中采用沿流向方向不同站位的總壓比等值線和繞渦核的流線的方式清晰表現出渦流場的存在，但由自適應局部加密的粘性網格得到的解明顯觀察到二次渦，并且主渦核的位置明顯更靠近翼根。因此，兩者的分析結論完全一致，即采用伴隨自適應局部加密后，粘性計算進行渦捕捉的能力明顯增強。另外，還容易注意到，由初始粘性網格計算得到的解還提前觀察到渦破裂。這與試驗觀察到的情況不太吻合［15］。

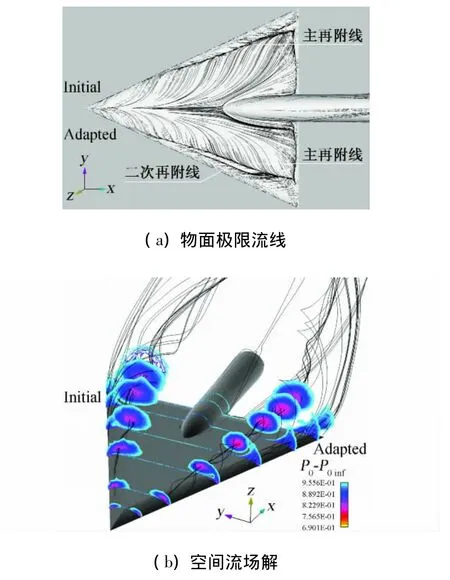
圖7 尖前緣65°三角翼模型的物面極限流線和空間流場解對比(粘性計算)Fig.7 Comparison of flow solutions between before and after adaptation for VFE-2 delta wing with sharp leading-edge(in viscous computation)

圖8比較了粘性計算得到的物面壓力系數分布。與無粘計算僅給出三個典型站位的結果不同，圖8給出了在試驗中所測量的所有站位數據的比較。其中，試驗結果包含兩類，一類由NASA Langley中心的跨音速風洞在雷諾數Re=6.0×106下進行試驗得到，一類由德國風洞協會的跨音速風洞在雷諾數Re=2.0×106下進行試驗得到，二者有較小的雷諾數效應差別。可以看到，由初始粘性網格得到的各站位上表面壓力系數分布與試驗值相差甚遠，主要表現在壓力系數吸力峰位置明顯沿展向朝翼尖位置偏移，而吸力峰峰值比試驗值偏小;與之相較，由自適應局部加密的粘性網格除了在x/c=0.2這一站位外，在其他四個站位都給出與試驗符合較好的結果。自適應局部加密對計算結果的改進非常明顯。在x/c=0.2這一站位，推測計算結果沒有明顯改善的原因是，兩套粘性網格在機翼前端附近的位置保持了基本一致的網格分辨率，而這一網格分辨率不足以保證在x/c=0.2站位給出與試驗符合良好的計算結果。可能的解決辦法是在這一區域附近進行手動加密以保證在機翼前端都有足夠的網格分布。

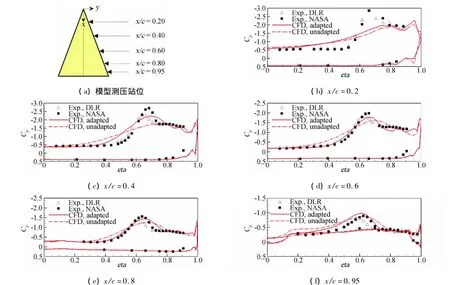
圖8 尖前緣65°三角翼模型在典型戰位的物面壓力系數分布與試驗值的對比(粘性計算)Fig.8 Comparison of pressure coefficient distributions with experimental data for VFE-2 delta wing with sharp leading-edge(in viscous computation)

4 結論

對基于伴隨方程的網格自適應技術的基本原理進行了研究，構造和實現了基于流場伴隨方程的非結構網格自適應探測器，采用局部加密網格的方法，建立了基于Euler方程的無粘伴隨自適應能力。對粘性計算，提出首先采用無粘計算和伴隨自適應生成網格分辨率好的初始網格，然后采用層推進方法生成粘性計算網格的求解策略。采用二維和三維經典算例對方法進行了驗證，并應用本文提出的求解策略對VFE-2尖前緣三角翼大攻角渦流場進行了數值模擬。計算結果表明，采用自適應技術能提高計算精度，尤其對三角翼大攻角渦流場這類存在大的分離和以渦主導的復雜流場，采用本文策略，可明顯改善預測結果，有效提高預測準確度。粘性計算時，在網格生成階段，采用Euler無粘計算進行伴隨自適應生成具有較好網格分辨率的初始四面體網格還可在一定程度上減小計算代價，提高計算效率。

［1］張來平，王志堅.三維復雜外形的非結構網格自動生成技術與應用［J］.計算物理，1999，16(5):552-558.

［2］BAI W，QIU Z，LI L.Recent efforts to establish adaptive hybrid grid computing capability at ACTRI［J］.Computational Fluid Dynamics journal，2007，7(4):438-449.

［3］WARREN G P，ANDERSON J T，THOMAS J T，KRIST S L.Grid convergence for adaptive methods［R］.AIAA paper 1991-1592，1991.

［4］PARK M A.Adjoint-based three-dimensional error prediction and grid adaptation［R］.AIAA paper 2002-3286，2002.

［5］NIELSEN E J.Adjoint-based algorithms for adaptation and design optimization on unstructured grids［A］.The 3rd East-West High-Speed Flow-field Conference［C］.Beijing，China，2005.

［6］LEE-RAUSCH E A，PARK M A，JONES W T，HAMMOND D P，NIELSEN E J.Application ofparalleladjoint-based error estimation and anisotropic grid adaptation for three-dimensionalaerospace configurations［A］.The 23rd AIAA Applied Aerodynamics Conference［C］.Toronto，Ontario，2005.

［7］VENDITTI D A.Grid adaptation for functional outputs of compressible flow simulations［D］.Massachusetts Institute of Technology，Cambridge，MA，2002.

［8］PIRZADEH S Z.An adaptive unstructured grid method by grid subdivision，local remeshing，and grid movement［R］.AIAA paper 1999-3255，1999.

［9］SHAROV D，FUJII K.Three-dimensional adaptive bisection of unstructured grids for transientcompressible flow computations［R］.AIAA paper 1995-1708，1995.

［10］TIMOTHY J B.Mesh generation:art or science［J］.Progress in Aerospace Sciences，2005，41:29-63.

［11］http://www.grc.nasa.gov/www/wind/valid/raetaf/raetaf.html

［12］http://www.grc.nasa.gov/www/wind/valid/m6wing/m6wing.html

［13］UMMEL D，REDEKER G.A new vortex flow experimentfor computer code validation［A］.RTO Symposium on"Advanced Flow Management:Part A-Vortex Flows and High Angle of Attack for Military Vehicles"［C］.Loen，Norway，2001.

［14］CHU J，LUCKRING J M.Experimental surface pressure data obtained on 65°delta wing across Reynolds number and Mach number ranges［R］.NASA TM-1996-4645，1996.

［15］KONRATH R，SCH?DER A，KOMPENHAS J.Analysis of PIV results obtained for the VFE-265°delta wing configuration at sub-and transonic speeds［A］.24th Applied Aerodynamics Conference［C］.San Francisco，California，2006.