雙下側(cè)定幾何二元混壓式進氣道的流場特征和氣動性能分析

謝旅榮，郭榮偉

(南京航空航天大學(xué)能源與動力學(xué)院，江蘇 南京 210016)

0 引言

超聲速混壓式進氣道兼有外部壓縮和內(nèi)部壓縮，它與外壓式進氣道相比外阻較小，而較內(nèi)壓式進氣道易于起動，在飛行馬赫數(shù)大于2.5時常被采用。二元進氣道由于結(jié)構(gòu)簡單，易于制造，且可以根據(jù)不同的任務(wù)需求選擇不同的布局形式，因此在一次性使用的吸氣式超聲速導(dǎo)彈中有較廣泛的應(yīng)用。進氣道在導(dǎo)彈上的布局方式除了影響導(dǎo)彈的氣動力特性外，對發(fā)動機特性尤其是進氣道性能同樣有著重要的影響［1-3］。但各種不同的布局方式均有優(yōu)缺點，關(guān)鍵是要根據(jù)導(dǎo)彈的工作特點選擇合適的布局。比如:歐盟的“流星”空空導(dǎo)彈選用雙下側(cè)布局，該布局方式便于機載，具有升阻比大、迎角性能好和橫向空間較小的優(yōu)點，但其側(cè)滑性能較差［4］;德國的“Armiger”反輻射導(dǎo)彈采用四個倒置二元進氣道叉形布局，由于減小了隔道高度從而降低了整體阻力，而且進氣道對稱分布利于飛控，但該布局形式下的進氣道其迎角/側(cè)滑特性較差，升阻比小［5-6］;法國的“ASMP”導(dǎo)彈采用的是兩個二元進氣道水平布局形式，進氣道壓縮面與彈身垂直，該布局形式的特點是升阻比高、迎角性能好，但其占用橫向空間大。因此，對于二元進氣道的氣動特性研究需結(jié)合其布局形式進行分析。

本文結(jié)合雙下側(cè)布局形式對二元進氣道的流場特征和氣動性能開展了研究。國外，雖然已經(jīng)有類似布局形式的導(dǎo)彈在研甚至已經(jīng)試飛成功(如“流星”導(dǎo)彈)，但是可能由于保密的原因鮮見相關(guān)文獻報導(dǎo)。國內(nèi)，對于定幾何二元混壓式進氣道設(shè)計和數(shù)值仿真也進行了較多的研究［7-9］，結(jié)合布局形式的研究主要針對叉形布局［10］和雙下側(cè)布局［11-13］。受到風(fēng)洞試驗條件的限制，結(jié)合雙下側(cè)布局形式獲得的進氣道性能參數(shù)主要是出口截面的。為了更深入的研究進氣道通道內(nèi)的流場特征和氣動性能，本文在文獻［4］基礎(chǔ)上對其開展數(shù)值仿真研究，分析了雙下側(cè)布局形式的兩個進氣道在不同飛行狀態(tài)下表現(xiàn)出的不同氣動性能，并結(jié)合通道內(nèi)的流場特征分析其原因。

1 數(shù)值模擬

1.1 物理模型

本文研究的二元混壓式進氣道為雙下側(cè)布局形式(如圖1所示)，工作馬赫數(shù)范圍是2.25～4.0，設(shè)計狀態(tài)為馬赫數(shù)Ma=3.0，迎角α=2°。具體型面參數(shù)請參見文獻［4］。

1.2 數(shù)值方法

計算中用有限體積法求解雷諾平均后的三維N-S方程，紊流模型選用Jones和Launder提出的標(biāo)準(zhǔn)k-ε模型，采用一階迎風(fēng)格式離散。由于紊流模型只適用于離開壁面一定距離的紊流區(qū)域，而在與壁面相鄰近的粘性邊界層中，必須考慮分子粘性的影響，k-ε方程亦要作相應(yīng)的修改，本文采用標(biāo)準(zhǔn)壁面函數(shù)。采用商業(yè)軟件Fluent5.0計算，收斂準(zhǔn)則為:連續(xù)方程、動量方程、能量方程以及k-ε方程的殘差至少下降3個數(shù)量級，且進氣道出口截面流量穩(wěn)定。

采用結(jié)構(gòu)化網(wǎng)格對整個計算域進行填充。由于研究對象幾何形體十分復(fù)雜，整個計算域內(nèi)被分為數(shù)十個子域進行網(wǎng)格生成，而后通過對接或耦合的方式形成一個整體。為了適合粘性計算以捕捉激波的需要，采用局部網(wǎng)格加密技術(shù)。由于在無側(cè)滑、滾轉(zhuǎn)下，計算對象結(jié)構(gòu)對稱、流場對稱，為了節(jié)省計算網(wǎng)格單元，取1/2的流動區(qū)域進行網(wǎng)格劃分，圖1給出了該物理模型壁面網(wǎng)格圖，計算網(wǎng)格數(shù)目約為56萬。計算側(cè)滑特性時采用全流動區(qū)域進行網(wǎng)格劃分，網(wǎng)格數(shù)目約為84萬。計算中采用的邊界條件有:壓力遠場邊界、壓力出口邊界、無滑移固壁邊界和對稱邊界條件(1/2計算域時)等。

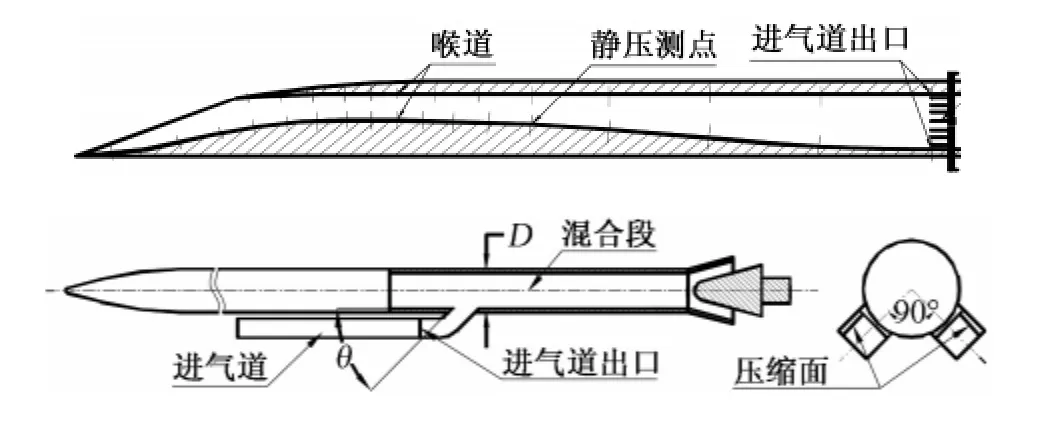
圖1 二元進氣道示意圖Fig.1 Sketch of inlet and model

圖2 壁面網(wǎng)格圖Fig.2 Grids of the model

2 結(jié)果與分析

對物理模型進行數(shù)值仿真的工況范圍為:來流馬赫數(shù) Ma=2.25～4.0，迎角 α =-6°～10°，側(cè)滑角 β=0°～6°。研究范圍內(nèi)，來流的單位雷諾數(shù)大于1×107。實驗是在南京航空航天大學(xué)NH-1風(fēng)洞中進行的。NH-1風(fēng)洞是暫沖式亞、跨、超聲速風(fēng)洞。試驗段截面尺寸為(0.6m×0.6m)。超聲速實驗時通過更換噴管獲得不同的來流馬赫數(shù)。在試驗馬赫數(shù)范圍內(nèi)來流的單位雷諾數(shù)大于2×107。

下面首先給出數(shù)值仿真與試驗結(jié)果對比驗證，試驗結(jié)果來自文獻［4］;然后分析數(shù)值仿真獲得的進氣道流場特征和氣動性能。

2.1 計算和試驗結(jié)果比較與分析

2.1.1 沿程靜壓分布曲線比較

圖3給出了在設(shè)計狀態(tài)下，計算和試驗獲得的進氣道處于超臨界狀態(tài)和臨界狀態(tài)時唇罩面和壓縮面沿程靜壓分布曲線。由圖可見，計算獲得的靜壓分布曲線和試驗相當(dāng)吻合。同時由圖3的靜壓分布曲線也可以看出，在進氣道出口截面稍上游處已經(jīng)出現(xiàn)結(jié)尾激波系，這是由于氣流拐彎段的影響造成的。圖4給出了未加出口反壓時不同縱剖面的計算馬赫數(shù)分布圖譜。可以看出在進氣道對稱面圖譜的出口截面上存在結(jié)尾激波系。在試驗中出口截面處為測量截面，受到總壓測量耙的影響，試驗得到的激波位置要比計算獲得的位置前移。同時由圖4拐彎段縱剖面的馬赫數(shù)分布圖譜可以看出，拐彎段內(nèi)出現(xiàn)了局部亞聲速區(qū)，但是被超聲速區(qū)將其與下游隔離，因此反壓必須提高到一定的值才能將進氣道內(nèi)已存在的結(jié)尾激波系往前推動。

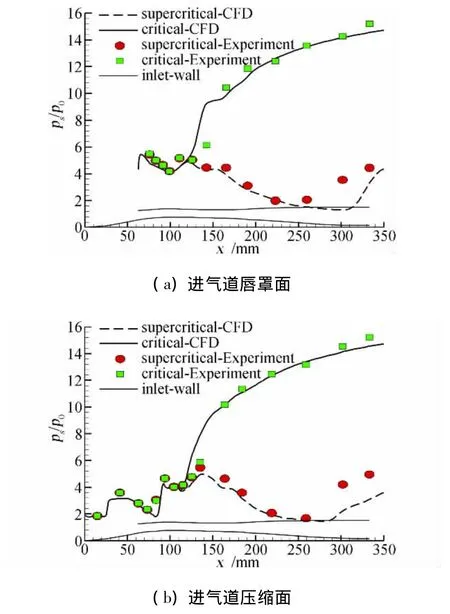
圖3 Ma=3.0時進氣道沿程靜壓分布曲線Fig.3 Distribution of static-pressure coefficient along duct at Ma=3.0

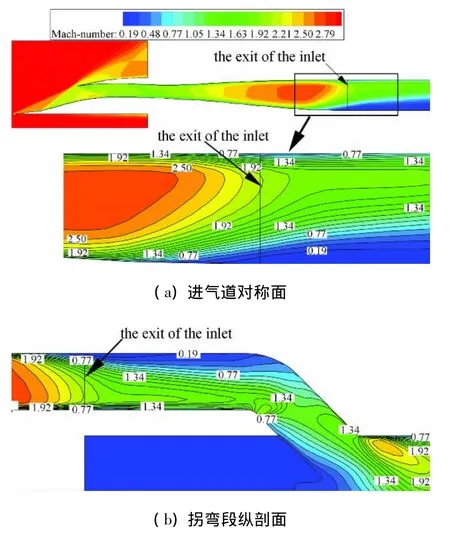
圖4 Ma=3.0，α=2°，β =γ=0°超臨界狀態(tài)下進氣道的馬赫數(shù)等值分布圖譜Fig.4 Mach number contours in the symmetry plane with supercritical operation at Ma=3.0，α=2°，and β =γ=0°

2.1.2 結(jié)尾激波系在超聲速收縮通道內(nèi)的流場特性

由文獻［4］試驗獲得的進氣道沿程靜壓分布曲線發(fā)現(xiàn)，當(dāng)進氣道結(jié)尾激波系位于喉道位置時，繼續(xù)加大反壓，結(jié)尾激波系可以穩(wěn)定在收縮通道內(nèi)。三維數(shù)值仿真獲得了同樣的結(jié)果。圖5給出了Ma=2.5，α=2°，β=γ=0°下結(jié)尾激波系在收縮通道內(nèi)和擴張通道內(nèi)時計算和試驗所獲得的進氣道沿程靜壓分布曲線，可見計算和試驗結(jié)果變化規(guī)律一致。圖6給出了對應(yīng)于圖5結(jié)尾激波系在收縮通道內(nèi)時進氣道對稱面馬赫數(shù)和流線分布圖。可以看出，由唇罩面和壓縮面上兩道斜激波和弱激波串組成的結(jié)尾激波系，已不同于傳統(tǒng)意義上混壓式進氣道的結(jié)尾正激波。根據(jù)數(shù)值仿真獲得的流場參數(shù)由流量連續(xù)公式計算，發(fā)現(xiàn)在物理喉道前方的結(jié)尾激波系附近(圖6.b所示的方框內(nèi))存在一個最小流通截面。這是因為當(dāng)結(jié)尾激波系被推過喉道時，在面積收縮比較小的收斂通道后段，由于激波/附面層相互干擾形成了小于物理喉道的氣動喉道。氣動喉道的形成致使結(jié)尾激波系能“站立”在收縮通道內(nèi)，保持穩(wěn)定的工作狀態(tài)。而且結(jié)尾激波系前馬赫數(shù)減弱使進氣道的性能高于臨界狀態(tài)時的數(shù)值。同樣的情況在更高馬赫數(shù)下也存在。數(shù)值仿真結(jié)果還發(fā)現(xiàn)，在Ma=2.25時結(jié)尾激波系不太容易在收縮通道內(nèi)停留，這是因為物理喉道面積是按Ma=2.25確定的，盡管在設(shè)計時留有一定的裕度，但若形成比喉道還小的氣動喉道時，易出現(xiàn)流量堵塞，從而將結(jié)尾激波系推出內(nèi)通道，導(dǎo)致進氣道不起動。

進氣道在來流馬赫數(shù)高于2.25時出現(xiàn)這種現(xiàn)象對于實際飛行是有利的，可以允許燃燒室壓力在臨界附近有一定范圍的上下波動，而不影響到進氣道捕獲的流量和工作穩(wěn)定性，有效提高了推進系統(tǒng)的穩(wěn)定工作裕度。

綜上所述，計算結(jié)果和風(fēng)洞試驗結(jié)果吻合良好，說明所采用的數(shù)值仿真方法可靠，結(jié)果可信，可作為該類進氣道研究的有力工具。

圖5 Ma=2.5不同反壓下的沿程靜壓分布曲線Fig.5 Distribution of static-pressure coefficient along duct at different back-pressure ratios

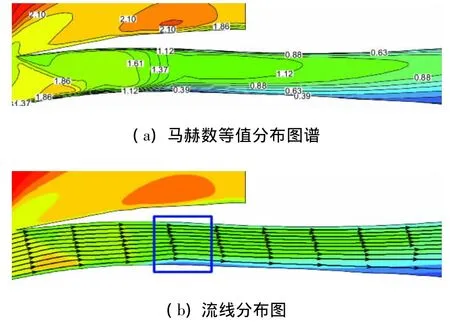
圖6 Ma=2.5下結(jié)尾激波系在收縮通道內(nèi)時進氣道對稱面馬赫數(shù)等值和流線分布圖Fig.6 Mach number contours and path lines in the symmetry plan when terminal shocks were moved in the convergent channels at Ma=2.5

2.2 進氣道流場特征和氣動性能分析

2.2.1 來流馬赫數(shù)變化的影響

圖7給出了α=2°，β=γ=0°時臨界狀態(tài)下進氣道出口截面總壓恢復(fù)系數(shù)和流量系數(shù)隨來流馬赫數(shù)的變化曲線。可以看出，計算和試驗規(guī)律一致，隨著來流馬赫數(shù)的增加，進氣道出口截面的總壓恢復(fù)系數(shù)逐漸降低。在低于設(shè)計馬赫數(shù)時，隨著來流馬赫數(shù)的增大，流量系數(shù)是升高的，到了設(shè)計馬赫數(shù)3.0后流量系數(shù)變化不大，基本保持在1.0。圖8分別給出了Ma=2.5和Ma=3.0，α =2°，β=γ =0°時臨界狀態(tài)下進氣道對稱面上的馬赫數(shù)等值分布圖譜。可以看出，Ma=2.5時斜激波波前馬赫數(shù)和喉道馬赫數(shù)相對于Ma=3.0時低，激波造成的總壓損失相對較小，因此Ma=2.5時進氣道的總壓恢復(fù)系數(shù)高于Ma=3.0時的數(shù)值。同時由于Ma=2.5時進口前的斜激波角度相對Ma=3.0時大，存在較多的超聲速溢流，導(dǎo)致流量系數(shù)低于Ma=3.0時的數(shù)值。

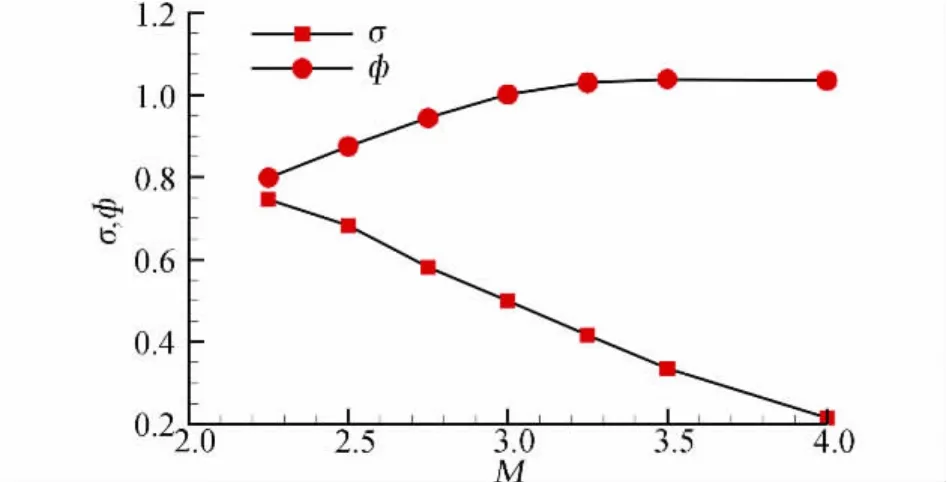
圖7 α=2°，β=γ=0°時進氣道總壓恢復(fù)系數(shù)和流量系數(shù)隨來流馬赫數(shù)變化曲線Fig.7 Total pressure recovery coefficient and mass flow ratio vs flight Mach number

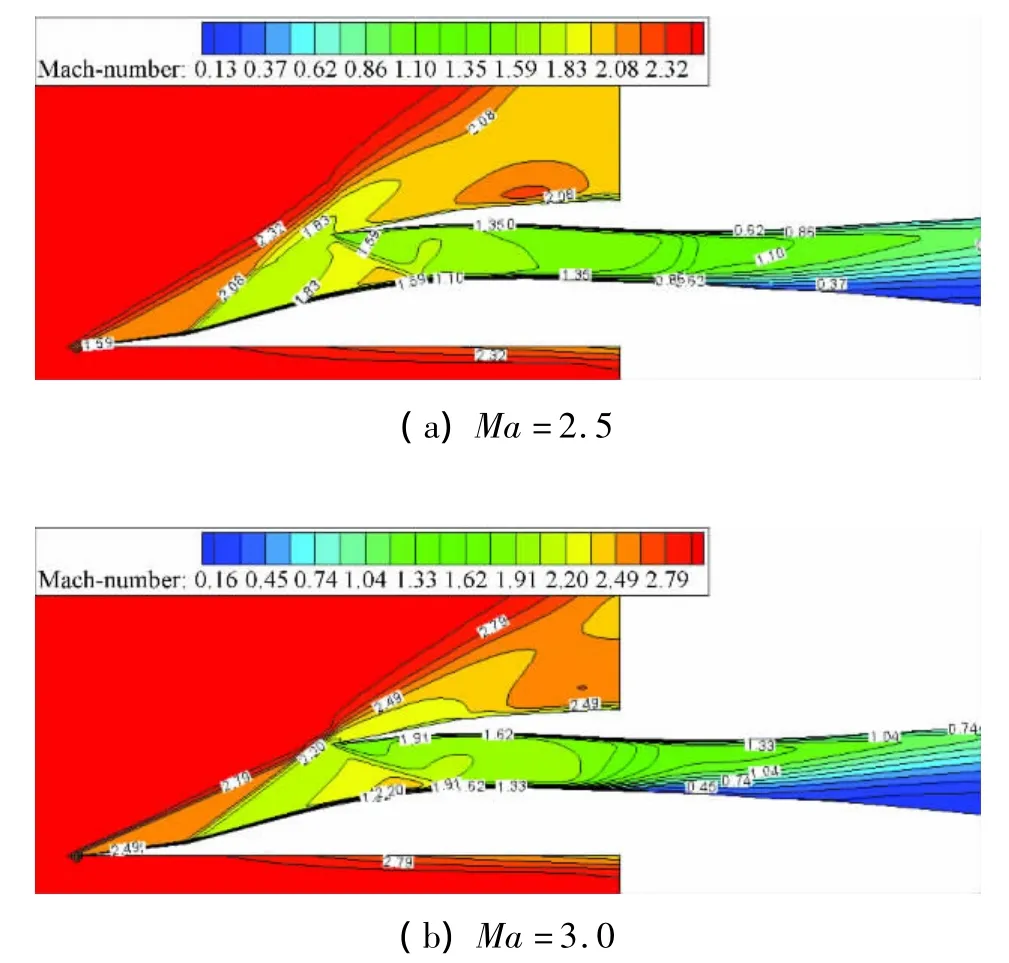
圖8 臨界狀態(tài)時進氣道對稱面馬赫數(shù)等值分布圖譜Fig.8 Mach number contours in the symmetry plane

2.2.2 迎角變化的影響

圖9給出了不同來流馬赫數(shù)下進氣道總壓恢復(fù)系數(shù)和流量系數(shù)隨迎角的變化曲線。可以看出，在研究范圍內(nèi)，隨著迎角的增大，進氣道的總壓恢復(fù)系數(shù)和流量系數(shù)在來流馬赫數(shù)為3.0和3.5時均是上升的。這說明雙下側(cè)布局方式的進氣道迎角性能好。圖10給出了Ma=3.0，β=γ=0°，α =2°和 α =8°時臨界狀態(tài)下進氣道對稱面的馬赫數(shù)等值分布圖譜。可看出，在α=8°時，進氣道壓縮面相對自由來流壓縮角增大，波后馬赫數(shù)降低，喉道馬赫數(shù)相對于α=2°時降低較大，結(jié)尾激波系損失減小，因此總壓恢復(fù)系數(shù)較高。

由圖9還可以看出，在Ma=2.5，α從-2°增加到4°時總壓恢復(fù)系數(shù)和流量系數(shù)是上升的。隨著迎角的繼續(xù)增大，總壓恢復(fù)系數(shù)和流量系數(shù)下降后基本保持不變。圖11給出了 Ma=2.5，α=6°，β=γ=0°時低反壓下進氣道對稱面上的馬赫數(shù)等值分布圖譜。可以看出，進氣道進口外唇罩出現(xiàn)一道類似弓形的激波，有亞聲速溢流，因此Ma=2.5，α=6°時進氣道總壓恢復(fù)系數(shù)和流量系數(shù)均有所下降。圖11還給出了該馬赫數(shù)下α=10°時進氣道對稱面上的馬赫數(shù)等值分布圖譜，可以看出，與α=6°比較，α=10°時進口前的脫體激波更遠離唇口，溢流更多。由圖11還可發(fā)現(xiàn)，盡管進口前出現(xiàn)脫體激波，但是收縮段內(nèi)的氣動通道總能調(diào)整到使進氣道的物理喉道加速到聲速。也正是因為在研究的迎角范圍內(nèi)，進氣道不起動后喉道總能達到聲速，而喉道前的激波損失由于來流馬赫數(shù)較低，總壓損失變化不大，進氣道的總壓恢復(fù)系數(shù)基本不變，因此能通過喉道的流量基本不變，流量系數(shù)的變化也不大。同樣的，在Ma=2.25，α =-4°～10°變化時，迎角增大到 2°后進氣道性能也下降，隨后基本保持不變，如圖9所示。

圖9 不同來流馬赫數(shù)下進氣道總壓恢復(fù)系數(shù)和流量系數(shù)隨迎角變化曲線Fig.9 Total pressure recovery coefficient and mass flow ratio vs angle of attack

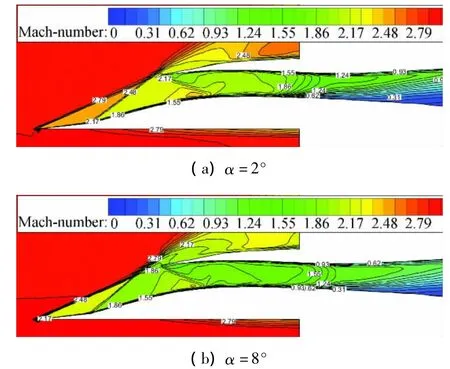
圖10 Ma=3.0時不同迎角下進氣道對稱面馬赫數(shù)等值分布圖譜Fig.10 Mach number contours in the symmetry plane at different angles of attack at Ma=3.0

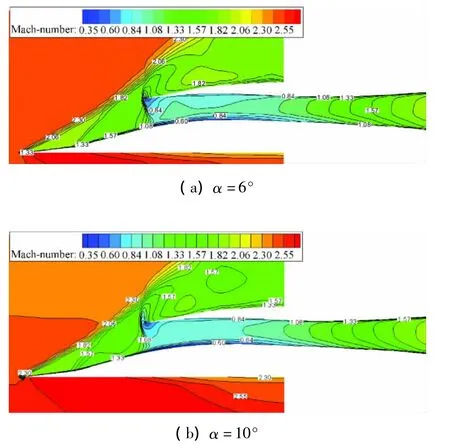
圖11 Ma=2.5時不同大迎角下進氣道對稱面馬赫數(shù)等值分布圖譜Fig.11 Mach number contours in the symmetry plane at different angles of attack at Ma=2.5

2.2.3 側(cè)滑角變化的影響

圖12分別給出了Ma=3.0和Ma=2.5，α=2°，γ=0°時進氣道總壓恢復(fù)系數(shù)和流量系數(shù)隨側(cè)滑角的變化曲線。可以看出，在研究范圍內(nèi)Ma=3.0時，隨著側(cè)滑角的增加，兩側(cè)進氣道的總壓恢復(fù)系數(shù)均是下降的，但是迎風(fēng)側(cè)進氣道相對于背風(fēng)側(cè)進氣道的性能下降更大;同時，隨著側(cè)滑角的增加，背風(fēng)側(cè)進氣道的流量系數(shù)是增加的，而迎風(fēng)側(cè)進氣道的流量系數(shù)下降較厲害。圖13 給出了 Ma=3.0，α =2°，β =4°，γ =0°時迎風(fēng)側(cè)處于臨界狀態(tài)下的兩側(cè)進氣道對稱面的馬赫數(shù)等值分布圖譜。可以看出，在迎風(fēng)側(cè)進氣道處于臨界狀態(tài)時，背風(fēng)側(cè)進氣道仍遠離喉道位置處在超臨界狀態(tài)，兩側(cè)進氣道結(jié)尾激波系位置存在差別。而且由于背風(fēng)側(cè)進氣道壓縮面相對來流壓縮角度增大，波后馬赫數(shù)較低，使進氣道結(jié)尾激波系強度相對弱，因此背風(fēng)側(cè)進氣道的總壓恢復(fù)系數(shù)高于迎風(fēng)側(cè)進氣道的。在研究的范圍內(nèi)，隨著側(cè)滑角的增大，背風(fēng)側(cè)進氣道雖然受彈身的影響增大，但是由于進氣道進口捕獲面積增大，因此其流量系數(shù)是增大的，而迎風(fēng)側(cè)正好相反，所以兩個進氣道的流量系數(shù)變化趨勢相反。

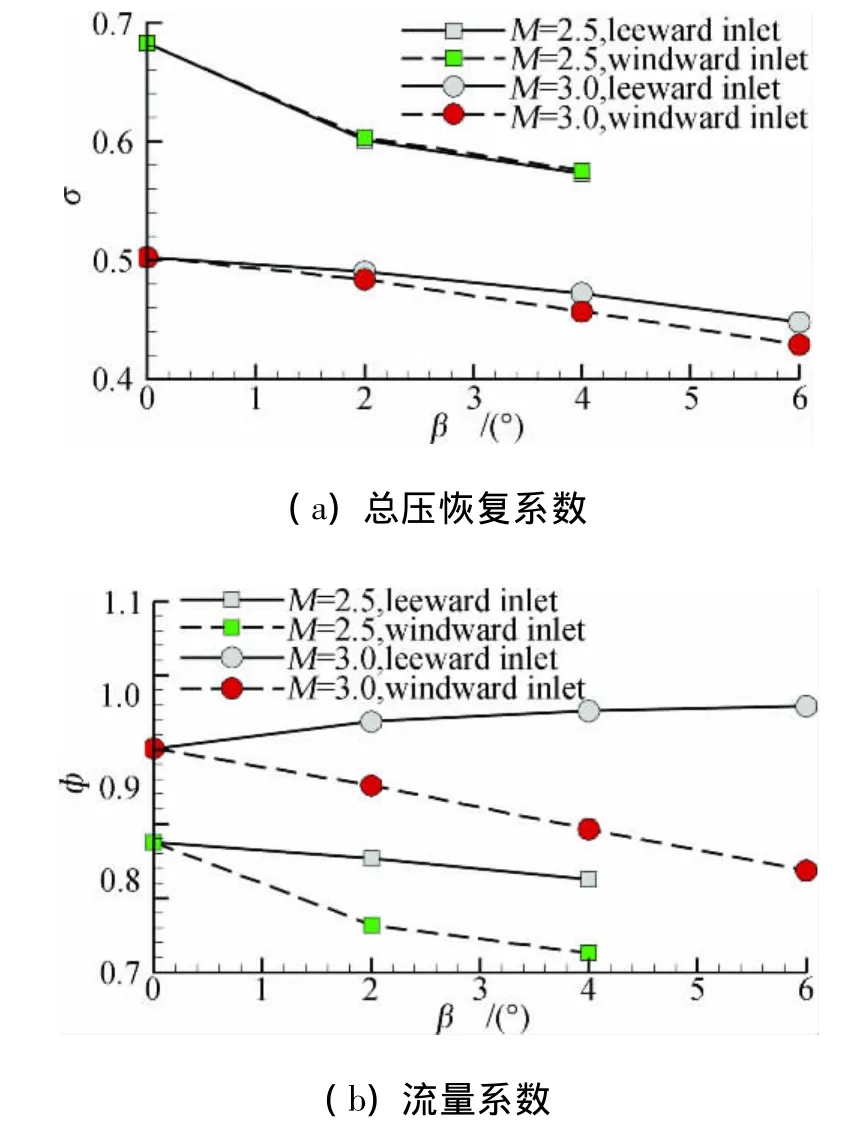
圖12 進氣道總壓恢復(fù)系數(shù)和流量系數(shù)隨側(cè)滑角變化曲線Fig.12 Total pressure recovery coefficient and mass flow ratio vs yaw angle

圖12給出的Ma=2.5時兩側(cè)進氣道性能的變化曲線與Ma=3.0的規(guī)律不太一致，背風(fēng)側(cè)進氣道的性能并未優(yōu)于迎風(fēng)側(cè)的性能。這是由于在Ma=2.5，β=2°時背風(fēng)側(cè)進氣道出現(xiàn)流量堵塞導(dǎo)致不起動，進口前增加了一道弓形激波，如圖14所示，因此總壓恢復(fù)系數(shù)和流量系數(shù)下降較大。隨著側(cè)滑角繼續(xù)增大，背風(fēng)側(cè)進氣道受到彈身的影響增大，進口前的總壓損失較大，而受到迎風(fēng)側(cè)進氣道承受反壓能力的限制，結(jié)尾激波系更遠離喉道致使總壓恢復(fù)系數(shù)也隨著下降。也正是由于喉道前的損失增大，進氣道不起動后盡管喉道仍能達到聲速，但其截面流通能力下降，從而使流量系數(shù)也隨之下降。

3 結(jié)論

由以上分析得到如下結(jié)論:

(1)當(dāng)來流馬赫數(shù)高于起動馬赫數(shù)2.25時，進氣道處于臨界狀態(tài)下，出口反壓繼續(xù)增大，在一定范圍內(nèi)，結(jié)尾激波系可以停留在收縮通道內(nèi)。

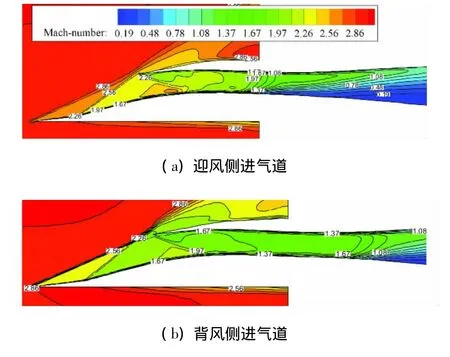
圖13 Ma=3.0，α=2°，β =4°，γ=0°時臨界狀態(tài)下兩側(cè)進氣道對稱面馬赫數(shù)等值分布圖譜Fig.13 Mach number contours in the symmetry planeof the inlets at Ma=3.0，α=2°，β =4°，γ=0°

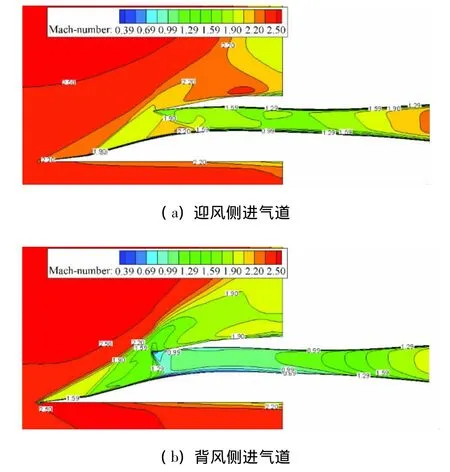
圖14 Ma=2.5，α=2°，β =2°，γ=0°時超臨界狀態(tài)下兩側(cè)進氣道對稱面馬赫數(shù)等值分布圖譜Fig.14 Mach number contours in the symmetry plane of the inlets at Ma=2.5，α =2°，β =2°，γ=0°

(2)隨著來流馬赫數(shù)的增加，進氣道斜激波損失和結(jié)尾激波損失增大，導(dǎo)致進氣道的總壓恢復(fù)系數(shù)隨之下降。而流量系數(shù)隨著來流馬赫數(shù)的增大而增大，到設(shè)計馬赫數(shù)及以上基本保持為1.0。

(3)一定范圍內(nèi)隨著迎角的增加進氣道的總壓恢復(fù)系數(shù)和流量系數(shù)均是提高的;但在低馬赫數(shù)大迎角情況下，進氣道易出現(xiàn)不起動現(xiàn)象;當(dāng)進氣道出現(xiàn)不起動時，進氣道的總壓恢復(fù)系數(shù)下降;繼續(xù)增大迎角，其總壓恢復(fù)系數(shù)和流量系數(shù)基本保持不變。

(4)由于共用同一燃燒室，在側(cè)滑情況下，背風(fēng)側(cè)進氣道受迎風(fēng)側(cè)進氣道承受反壓能力下降的限制，兩側(cè)進氣道的性能均下降。隨著側(cè)滑角的增大，迎風(fēng)側(cè)進氣道的流量系數(shù)逐漸降低，背風(fēng)側(cè)進氣道則是增大。當(dāng)?shù)婉R赫數(shù)大側(cè)滑角下進氣道不起動時，其總壓恢復(fù)系數(shù)和流量系數(shù)均下降。

(5)通過與風(fēng)洞試驗結(jié)果比較，表明所采用的數(shù)值方法是可信的，可作為該類進氣道研究的有力工具。

［1］CLYDE H.Aerodynamic characteristics of a series of twin-inlet air-breathing missile configurations(Ⅱtwo-dimensional inlets at supersonic speeds)［R］.NASA TM-84559，1983.

［2］謝旅榮，郭榮偉.雙下側(cè)布局二元超聲速進氣道摻混氣動特性［J］.航空學(xué)報，2007，28(6)∶1287-1295.

［3］李博，梁德旺.混壓式進氣道與彈體一體化流場數(shù)值模擬［J］. 推進技術(shù)，2002，23(4)∶307-310.

［4］謝旅榮，郭榮偉.雙下側(cè)定幾何二元混壓式超聲速進氣道的風(fēng)洞試驗［J］.航空學(xué)報，2009，30(6)∶1000-1006.

［5］萬大為，郭榮偉.定幾何二元倒置“X”型混壓式超聲速進氣道實驗［J］.南京航空航天大學(xué)學(xué)報，2007，39(3)∶277-281.

［6］WAN D W，GUO R W.Experimental investigation of a fixed-geometry two geometry two dimensional mixed-compression supersonic inlet with sweepforward high-light and bleed slot in a"X"-type layout［J］.Chinese Journal of Aeronautics，2007，20(4)∶304-312.

［7］王國輝，李進賢，蔡體敏.二元混壓超聲速進氣道三維流動數(shù)值分析［J］.推進技術(shù)，2001，22(2)∶118-121.

［8］洛廣琦，鄭九州，宋頔源.考慮附面層影響的二元混壓式進氣道設(shè)計［J］.航空動力學(xué)報，2009，24(9)∶2063-2068.

［9］劉曉偉，何國強，秦飛.寬馬赫數(shù)固沖二元進氣道設(shè)計與研究［J］.宇航學(xué)報，2008，29(5)∶1577-1582.

［10］鮑福廷，李進賢，趙飛.固沖發(fā)動機雙下側(cè)二元進氣道設(shè)計研究［J］. 西北工業(yè)大學(xué)學(xué)報，2002，20(4)∶590-593.

［11］白鵬，朱守梅，孟宇鵬，等.沖壓發(fā)動機進氣道和摻混段節(jié)流特性數(shù)值研究［J］.推進技術(shù)，2004，25(6)∶503-507.

［12］謝旅榮，郭榮偉.一種定幾何混壓式二元進氣道的再起動特性研究［J］.航空動力學(xué)報，2007，23(2)∶590-593.

［13］麻肖妃，謝旅榮，郭榮偉.雙下側(cè)布局帶泄流腔二元進氣道試驗［J］.航空動力學(xué)報，2010，25(8)∶1818-1824.