轉捩對風力機翼型和葉片失速特性影響的數值模擬

鐘 偉，王同光

(南京航空航天大學江蘇省風力機設計高技術研究重點實驗室，江蘇 南京 210016)

0 引言

風力機翼型的氣動特性是風力機葉片設計的基礎輸入參數。要獲得翼型在多個雷諾數和較大迎角范圍內的完整風洞實驗數據，所需費用較高。計算流體力學(CFD)數值模擬技術逐漸成為獲取和研究翼型氣動特性的一種更經濟快捷的選擇。在眾多風力機翼型中，S809翼型［1］是最重要的風力機空氣動力學研究對象之一，因為它不僅風洞實驗數據充分，而且是美國國家可再生能源實驗室(NREL)開展的水平軸風力機非定常空氣動力學系列實驗［2］的葉片翼型。S.L.Yang等人［3］于1994年最早對S809翼型進行了全湍流數值模擬。在附著流動階段，升力系數與實驗結果基本吻合，只在個別迎角下出現壓力分布局部不符;但阻力系數遠大于實驗值。Walter P.Wolfe等人［4］于1997年使用指定轉捩點的方式對S809翼型進行了數值模擬。附著流動階段的阻力系數誤差相對全湍流模擬顯著下降，壓力分布局部不符的問題也不再存在。他們的結果表明，轉捩對翼型附著流動狀態下的氣動特性有影響，值得加以研究。

風力機葉片的氣動特性與其基于的翼型的氣動特性有緊密聯系。在對S809翼型的數值模擬研究基礎上，研究人員對基于該翼型的NREL Phase VI葉片開展了大量的數值模擬研究。Phase VI實驗于2000年春季在世界上最大的風洞——NASA Ames研究中心24.4m×36.6m全尺寸風洞中進行，是迄今為止可信度最高測量數據最全面的風力機空氣動力學實驗。在實驗結果公布之前，NREL即組織了世界上多名風力機空氣動力學研究人員采用多種方法進行了計算盲比。然而盲比的結果出乎意料的不理想［5］。其中與實驗數據最接近的結果來自CFD數值模擬［6］，但仍然存在較大誤差。此后，眾多學者采用多種解算器和計算模型對Phase VI葉片進行了CFD數值模擬［7-9］。這些結果較NREL盲比結果有所改進，但距離與實驗數據的較好吻合仍然有相當的距離，且至今未有對造成數值模擬誤差的原因形成合理解釋。以上數值模擬都是全湍流模擬，關于轉捩對葉片氣動特性影響的研究很少。

R.B.Langtry等人［10］于2006 年使用 F.R.Menter等人發展的 Gamma-Theta轉捩模式［11］對 S809翼型和Phase VI葉片進行了數值模擬。他們預測的翼型轉捩點位置與實驗吻合，且捕捉到了層流分離和湍流再附形成的分離泡，闡述了轉捩對S809翼型在附著流動狀態下氣動特性的影響，但還缺乏對翼型失速特性影響的研究。他們對Phase VI葉片進行的轉捩模擬獲得的扭矩值在20m/s風速下相對全湍流模擬更接近實驗值，在其它風速下則與全湍流模擬差別不明顯。但其在20m/s風速下全湍流模擬得到的扭矩值本身高于實驗值太多，誤差明顯大于其他學者的數值模擬結果，這削弱了其關于轉捩影響的結論的說服力。

本文在以上學者的研究基礎上，使用Gamma-Theta轉捩模式對S809翼型和Phase VI葉片進行了數值模擬，著重研究了轉捩對翼型和葉片失速特性的影響。

1 數值模擬方法

1.1 控制方程

求解的控制方程組為守恒型非穩態不可壓縮雷諾平均的Navier-Stokes方程，其在靜態坐標系下的表達式為:

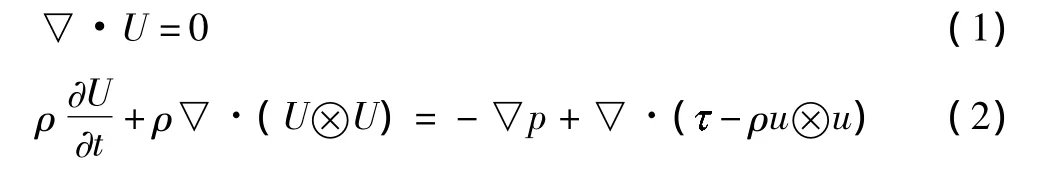
式中ρ為空氣密度，U為平均速度矢量，u為脈動速度矢量，p為靜壓，為分子應力張量，ρu?u為雷諾應力。

采用有限體積方法進行CFD定常求解。方程離散采用二階迎風格式。

1.2 湍流模型與轉捩模式

湍流模擬采用切應力輸運(shear stress transport，SST)模型。該湍流模型是公認的較好的線性渦粘性模型，對邊界層流動和分離流動都能有較好的模擬效果。采用的轉捩模式為Gamma-Theta轉捩模型。該湍流模型和轉捩模型均由F.R.Menter提出，被結合使用。受篇幅限制，本文僅列出Gamma-Theta轉捩模型的輸運方程。關于該湍流模型和轉捩模型的詳盡描述及本文所列輸運方程中各參數的含義可參考相關文獻［11］。

Gamma-Theta轉捩模型中間歇因子γ和轉捩動量厚度雷諾數～Reθt的輸運方程分別為:

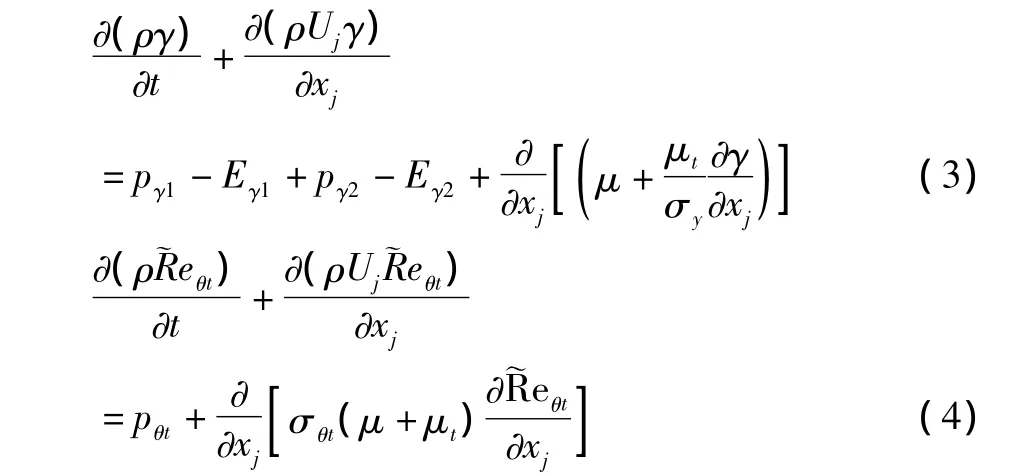
該轉捩模型的求解順序為:根據上一個時間步的平均流場及 γ值，通過的輸運方程求出，然后通過間歇因子γ的輸運方程求解出當前時間步的γ，最后通過有效粘性系數γut作用于平均流場。

1.3 多參考系模型(MFR)

在對風力機葉片的數值模擬中，葉片相對地面坐標系是旋轉的，流場相對地面坐標系是非穩態流動。如果直接以地面坐標系為參考系進行求解，需要對葉片的實際運動進行非穩態模擬，且涉及網格的運動問題，計算量和難度都較靜止物體的求解要大。如果定義參考系跟隨葉片一起旋轉，則在此旋轉坐標系下流場轉化為定常狀態。因此，考慮采用旋轉坐標系的方法來模擬葉片的轉動。但為了正確地設置邊界條件，又需要遠場邊界在計算坐標系下是靜止的。為了解決模擬葉片旋轉與正確設置遠場邊界條件這一矛盾，采用多參考系模型(MFR)，將計算域分為內外兩個區域，包圍葉片的內區采用旋轉坐標系，靠近遠場的外區則使用地面坐標系。

在實際解算過程中，處于旋轉坐標系區域內的流體被賦予了一個與坐標系旋轉速度相反的旋轉速度。另外，還需要考慮離心力和科氏力的影響，在動量方程中添加相關源項。離心力和科氏力的源項分別為:

1.4 計算域、網格與邊界條件

本文S809翼型的數值模擬不考慮翼型實驗的風洞洞壁影響(用作參考的OSU實驗報告［12］的數據已經過洞壁干擾修正)，計算域外邊界為開口大氣。計算域內網格拓撲結構為C型，翼型表面共430個網格點，首層網格高度保證y+≤1。計算域入口邊界距離翼型前緣10倍弦長，出口邊界距離翼型后緣15倍弦長，上下邊界距離翼型10倍弦長。入口邊界指定來流的速度矢量和湍流強度，出口邊界指定出口靜壓。

由于工藝原因，風洞實驗模型的尾緣不可能是完全尖的，而是稍有鈍化的。因此，本文用于模擬的S809翼型尾緣也按照OSU實驗報告描述的方法進行了微小尺度的鈍化。

Phase VI葉片數值模擬的計算域如圖1所示，分為葉片附近的旋轉坐標系區域和外層的地面坐標系區域，也沒有考慮風洞洞壁的影響。計算域的外邊界分為迎風的入口邊界、背風的出口邊界和平行于來流的開口邊界。入口邊界指定來流的速度矢量和湍流強度，出口邊界指定出口靜壓，開口邊界允許氣流流入或流出。應用了旋轉周期邊界，以利用風輪的軸對稱特點節省網格數。對于兩葉片的Phase VI風輪，周期邊界的應用使得計算域只有實際區域的一半，從而使網格數和計算量減半。計算域入口邊界與葉片的距離為8L(L為葉片展長)，出口邊界距離葉片15L，開口邊界距離葉片10L。葉片表面首層網格高度保證y+≤1。對不同網格密度的模型進行了網格無關性測試，發現網格單元總數大于450萬時達到網格無關性要求，因此選用網格單元總數為450萬的模型用于數值模擬。

NREL的報告中沒有描述Phase VI葉片在加工過程中尾緣的實際鈍化情況。考慮到工藝上可達到的尾緣尖銳程度應當是相近的，本文用于模擬的Phase VI葉片模型的尾緣按照與S809翼型相同的方法進行了微小尺度的鈍化。

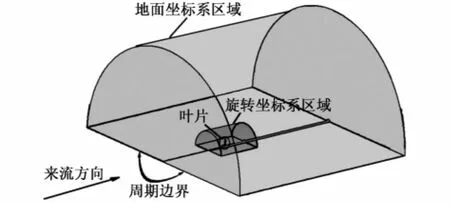
圖1 Phase VI葉片數值模擬的計算域Fig.1 Simulation domain for blade Phase VI

2 S809翼型數值模擬結果

考慮到Phase VI實驗中葉片各剖面的工作雷諾數大部分處于1×106附近，為使S809翼型的數值模擬結果與Phase VI葉片的數值模擬結果互相具有參考性，本文對S809翼型數值模擬的雷諾數選擇為1×106。

圖2顯示了雷諾數1×106下S809翼型的實驗值、SST模型轉捩模擬結果和全湍流模擬結果。升力系數的實驗值在迎角0°～8°之間基本呈線性增長，8°～16°之間變得平緩，16°～20°急劇下降，20°以后再次上升。結合OSU實驗報告中S809翼型在各迎角下的壓力分布可以判斷，以上四個階段的流場基本特征分別為:附著流動狀態、尾緣分離的發生和發展、尾緣分離向完全分離的急劇轉變、完全分離流動狀態。其中除附著流動狀態以外的其它三個狀態可以分別被稱為輕失速狀態、輕失速向深失速的轉變、深失速狀態。

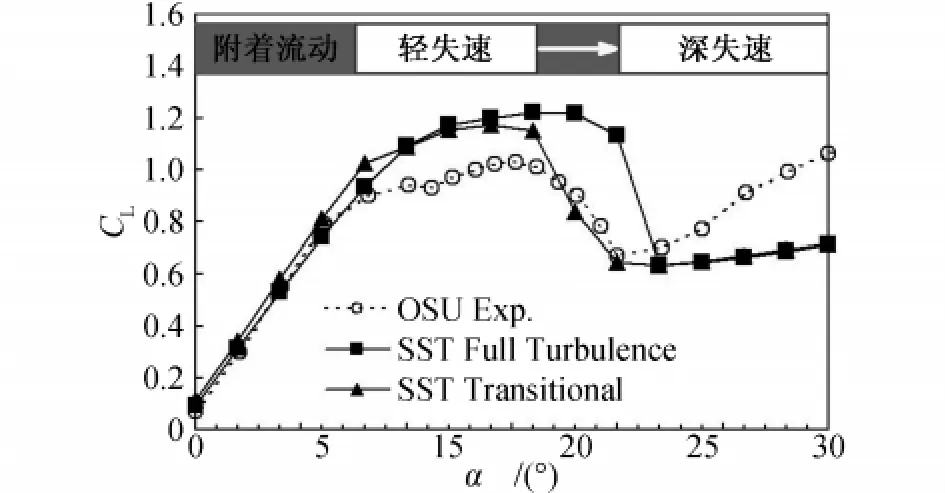
圖2 S809翼型的升力系數(Re=1×106)Fig.2 Lift coefficient of airfoil S809(Re=1×106)

全湍流模擬的升力系數在附著流動階段與實驗結果吻合，在輕失速階段則明顯高于實驗值。這與其他學者采用包括SST模型在內的各種線性渦粘性模型開展數值模擬得到的結果是一致的。隨著迎角的繼續增大，全湍流模擬由輕失速向深失速的轉變較實驗結果顯著延遲，當實驗升力系數已因深失速而急劇下降時，全湍流模擬的升力系數仍處于高位，導致在迎角20°左右出現很大的升力系數計算誤差(高達約80%)。進入深失速以后，全湍流模擬的升力系數低于實驗值，這可能是兩方面原因導致的:一方面，大迎角下翼型本身對風洞的阻塞度增大，同時深失速狀態下翼型背風面的漩渦的尺度比翼型本身還大，洞壁干擾的影響大增導致實驗數據的洞壁干擾修正不足;另一方面，深失速狀態的實際流場為非定常，且分離漩渦內湍流的發展對流場結構有較大影響，當前的定常數值模擬只是實際流場的平均近似，湍流模型也不足以準確描述漩渦內的湍流發展。

相對全湍流模擬結果，轉捩模擬的升力系數在附著流動階段略微高一些。關于轉捩在該階段的影響，Wolfe等人［4］和 R.B.Langtry 等人［10］已有相關論述，本文不再展開分析。

當迎角增大至輕失速狀態后，轉捩模擬的升力系數逐漸低于全湍流模擬結果，但仍然明顯高于實驗值。這說明轉捩對S809翼型輕失速狀態的氣動特性有一定影響，但并不是造成數值模擬升力系數偏高的主要原因。圖3顯示了迎角16°下翼型周圍的流線。由圖可見，轉捩模擬和全湍流模擬的流場結構基本相同，只在流場細節上有兩點差異:一是轉捩模擬結果在前緣附近存在層流分離泡，而全湍流模擬結果不存在;二是轉捩模擬的流動分離區域稍大于全湍流模擬結果。

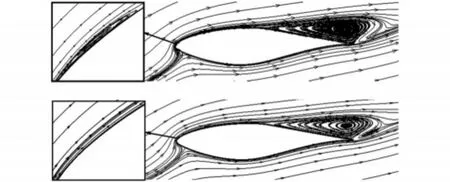
圖3 迎角16°下S809翼型周圍流線(上:轉捩，下:全湍流)Fig.3 Streamlines around airfoil S809 at AOA 16°(up:transitional，down:full turbulence)

迎角16°～22°是轉捩模擬和全湍流模擬的升力系數差別最大的區域。轉捩模擬的升力系數與實驗值同步急劇下降，全湍流模擬的升力系數則在更大的迎角下才開始急劇下降。圖4顯示了迎角20°下翼型周圍的流線。由圖可見，轉捩模擬和全湍流模擬的流場結構有明顯不同:前者發生了從前緣到尾緣的完全分離，漩渦區域覆蓋了翼型的整個背風面;后者在前緣附近仍然為附著流動，漩渦尺度較前者明顯小。結合16°迎角下轉捩模擬中觀察到的前緣分離泡推測，轉捩模擬比全湍流模擬更早進入深失速的原因可能是前緣層流分離轉捩后因逆壓梯度較大不能再附，與已經推進至接近前緣的尾緣分離渦一同促成了完全分離的發生。

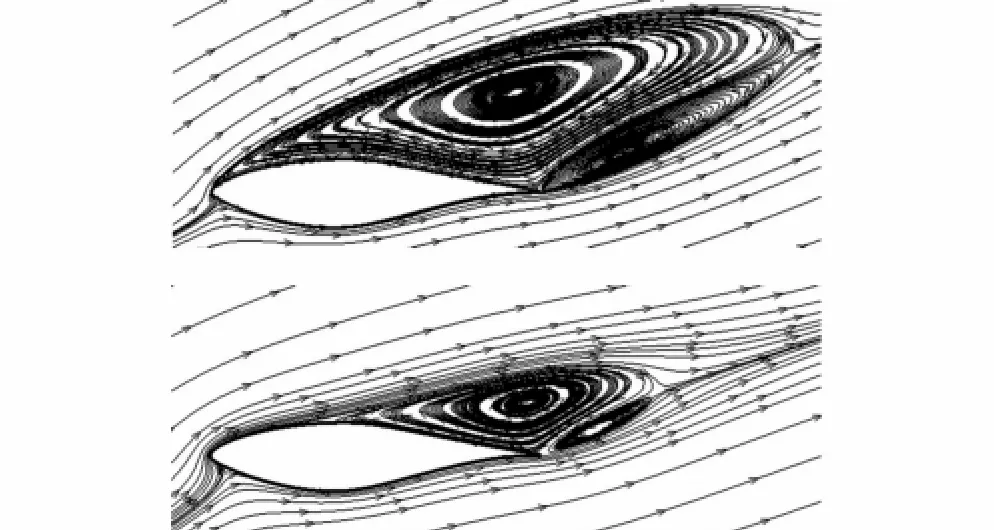
圖4 迎角20°下S809翼型周圍流線(上:轉捩，下:全湍流)Fig.4 Streamlines around airfoil S809 at AOA 20°(up:transitional，down:full turbulence)

流動分離是附面層不能克服逆壓梯度而在其底層發生“返流”導致的，附面層內速度剖面的豐滿程度決定了其可以抵御的逆壓梯度的強弱，而速度剖面的形狀又與附面層的發展歷程有關。因此，翼型的尾緣分離是受從前緣駐點開始的附面層發展歷程影響的。在失速階段，轉捩模擬與全湍流模擬獲得的附面層發展歷程中最顯著的區別在于前緣分離泡的存在。為了進一步分析前緣分離泡的影響，作者開展了指定轉捩點的數值模擬，將十分接近前緣的地方(即將發生層流分離處)設定為強制轉捩點，以避免層流分離泡的形成。在失速范圍內，強制轉捩的數值模擬結果與全湍流模擬結果相近。這說明，前緣分離泡的存在與否對翼型的失速特性有著決定性的影響。因此，轉捩模擬與全湍流模擬在S809翼型失速特性上的差異，與其說是轉捩的影響，不如說是前緣層流分離泡的影響更確切。

迎角大于22°以后，轉捩模擬與全湍流模擬獲得的升力系數一致。在這樣大的迎角下，緊鄰翼型前緣的逆壓梯度非常大，以至于無論層流邊界層還是湍流邊界層都無法抵御，在幾乎相同的位置發生分離，因此翼型表現出來的氣動特性也幾乎相同。

3 Phase VI葉片數值模擬結果

風速7m/s～25m/s下Phase VI風輪扭矩的實驗值［5］、轉捩模擬和全湍流模擬的數值模擬結果如圖5所示。在風速為7m/s和9m/s時，轉捩模擬和全湍流模擬結果相近，與實驗值基本吻合;在風速9m/s～20m/s之間，全湍流模擬結果明顯高于實驗值，轉捩模擬結果則與實驗值接近。當風速繼續增大到20m/s以上，轉捩模擬和全湍流模擬的結果一致。

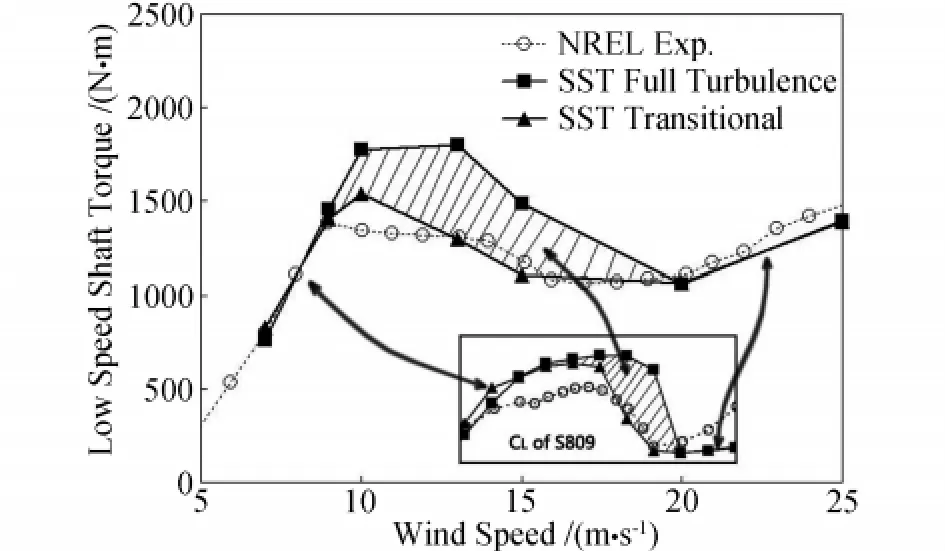
圖5 Phase VI風輪的扭矩Fig.5 Low speed shaft torque of Phase VI rotor

葉片各個剖面的當地迎角是隨著來流風速的增大而增大的。葉片氣動力隨風速的變化與S809翼型氣動力隨迎角的變化必然存在一定的關聯。圖5中同時畫出了S809翼型的升力系數。通過對比可見，轉捩模擬與全湍流模擬結果的差異在Phase VI風輪的扭矩與S809翼型的升力系數之間呈現出很強的相似性:小風速(小迎角)時，轉捩模擬與全湍流模擬的風輪扭矩(翼型升力系數)相近;隨著風速(迎角)的增大，轉捩模擬結果明顯低于全湍流模擬結果;當風速(迎角)繼續增大至某一值以后，轉捩模擬與全湍流模擬的結果再次一致。

圖6顯示了Phase VI葉片在風速9m/s、13 m/s和20 m/s時吸力面的摩擦力線，這幾個風速下的流場結構代表了葉片從輕失速到深失速狀態的典型流態。

風速9m/s時，葉片吸力面存在局部尾緣分離，越靠近葉根分離越嚴重，葉尖附近則為附著流動狀態(說明葉片剖面迎角由葉根至葉尖逐漸減小)。轉捩模擬和全湍流模擬的分離區域大小相近，但轉捩模擬描述了層流分離泡的存在。這與S809翼型模擬中輕失速階段的情況是相符的。

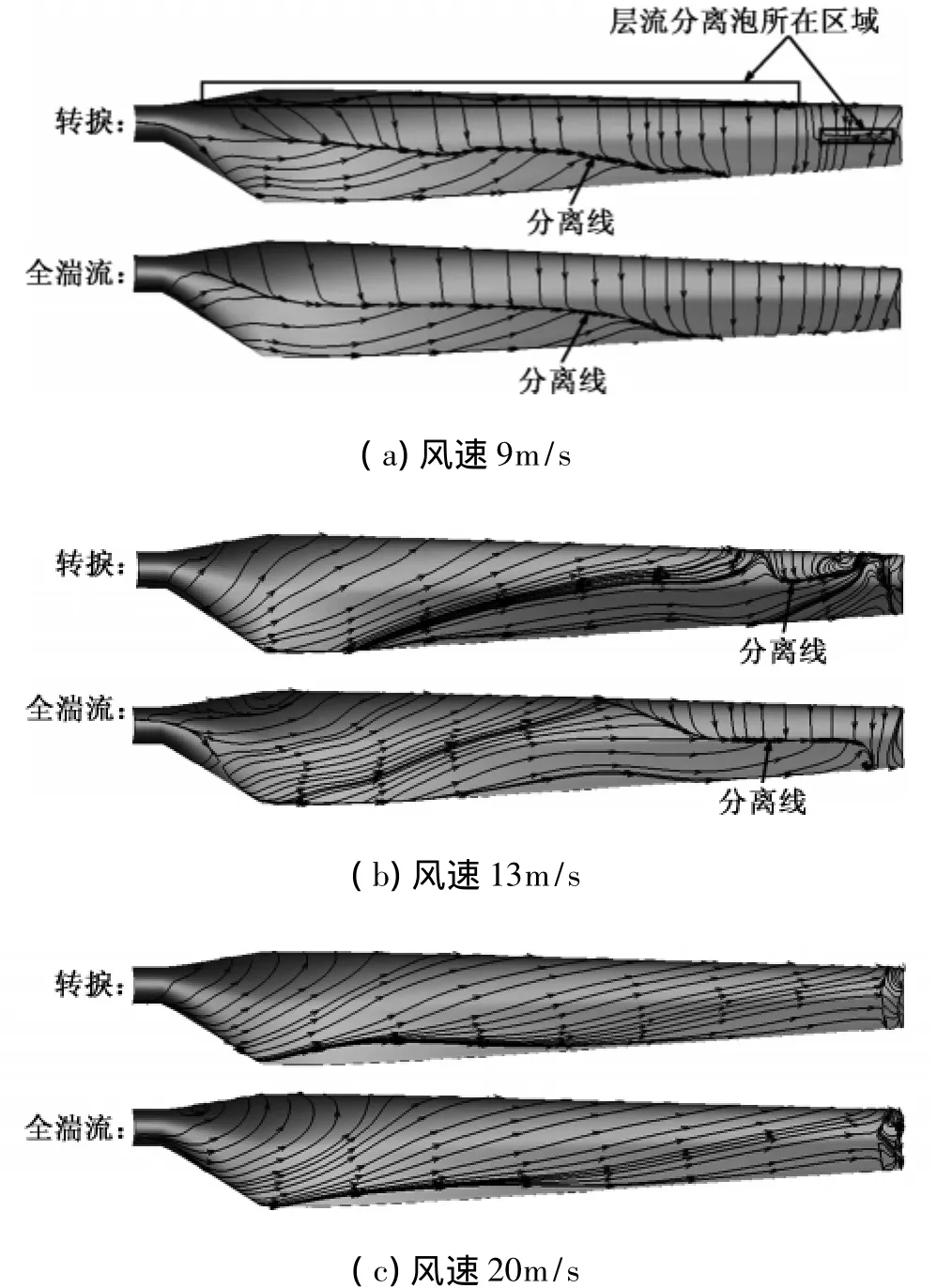
圖6 Phase VI葉片吸力面的表面摩擦力線Fig.6 Friction lines on suction surface of blade Phase VI

風速13m/s時，轉捩模擬的葉片吸力面除葉尖局部外的大部分區域已處于完全分離流動狀態(深失速);全湍流模擬結果則在葉尖附近存在大一些的尾緣分離流動(輕失速)區域，完全分離(深失速)的區域相對轉捩模擬結果小一些。這與S809翼型模擬中轉捩模擬更早進入深失速的情況是相符的，也是轉捩模擬獲得的風輪扭矩在中等風速下低于全湍流模擬結果并與實驗值更接近的主要原因。

風速20m/s時，轉捩模擬和全湍流模擬的葉片吸力面均已處于完全分離流動狀態(深失速)，兩者獲得的流場細節未見明顯差別。這與S809翼型模擬中轉捩模擬和全湍流模擬結果在深失速以后變得一致的情況是相符的。

以上關于各風速下流場形態的分析進一步將葉片模擬結果與翼型模擬結果聯系起來。說明轉捩對葉片失速特性和翼型失速特性產生影響的方式是相似的，都是通過前緣層流分離泡的作用體現出來。不過需要說明的是，本文轉捩模擬獲得的Phase VI風輪扭矩與實驗數據符合較好，除了考慮轉捩使葉片進入深失速的時機與實驗更接近外，還因為輕失速剖面的正誤差和深失速剖面的負誤差相互有所抵消，因此不能認為轉捩的引入完全解決了Phase VI葉片氣動力預測不準確的難題。

4 結論

本文采用Gamma-Theta轉捩模型對S809翼型和NREL Phase VI葉片進行了氣動力數值模擬，分析了轉捩對該翼型和葉片失速特性的影響。S809翼型的數值模擬結果表明:在輕失速階段，轉捩模擬得到的升力系數稍低于全湍流模擬結果，仍明顯高于實驗值;在輕失速向深失速的轉變階段，轉捩模擬的升力系數與實驗值同步急劇下降，而全湍流模擬結果進入深失速的時機明顯滯后;進入深失速以后，轉捩模擬與全湍流模擬獲得的升力系數一致。結合典型迎角下的流場細節，發現前緣層流分離泡的存在影響了翼型的失速特性，導致深失速更早發生。

Phase VI葉片的數值模擬與S809翼型的數值模擬結果之間存在較顯著的關聯性。小風速時轉捩模擬與全湍流模擬結果相近;中等風速時轉捩模擬得到的風輪扭矩顯著低于全湍流模擬結果，更接近實驗值;大風速時轉捩模擬與全湍流模擬的結果一致。這與翼型數值模擬中隨著迎角的增大，轉捩模擬與全湍流模擬得到的升力系數的變化規律是相符的。結合對典型風速下葉片表面流動狀態的分析，認為轉捩對葉片失速特性和翼型失速特性產生影響的方式是相似的，都是通過前緣層流分離泡的作用體現出來。

綜上所述，本文認為與層流和轉捩相關的前緣分離泡的存在會導致S809翼型和Phase VI葉片失速特性的變化，特別是會導致深失速的更早發生。考慮到前緣分離泡對邊界層流動的作用機制并不因翼型或葉片的不同而不同，因此認為以上結論對其它翼型和葉片同樣適用。但另一方面，由于S809翼型和Phase VI葉片流動顯示實驗結果的缺乏，導致本文數值模擬中捕捉到的前緣層流分離泡暫不能得到實驗驗證。不過這并不影響本文關于前緣層流分離泡對翼型和葉片失速特性影響的結論在性質上的正確性。

［1］DAN M，SOMERS.Design and experimental results for the S809 airfoil［R］.Colorado:National Renewable Energy Laboratory，1997.

［2］HAND M M，SIMMS D A，FINGERSH L J，etal.Unsteady aerodynamics experiment phase VI:wind tunnel test configurations and available data campaigns［R］.Colorado:National Renewable Energy Laboratory，2001.

［3］YANG S L，CHANG Y L，ARICI O.Incompressible Navier-Stokes computation of the NREL airfoils using a symmetric total variational diminishing scheme［J］.Journal of solar energy engineering，1994，116:174-182.

［4］WALTER P W，STUART S O.CFD calculations of S809 aerodynamic characteristics［R］.AIAA 97-0973，1997.

［5］SIMMS D，SCHRECK S，HAND M，et al.NREL unsteady aerodynamics experiment in the NASA-Ames wind tunnel:a comparison of predictions to measurements［R］.Colorado:National Renewable Energy Laboratory，2001.

［6］S?RENSEN N N，MICHELSEN J A，SCHRECK S.Navier-Stokes predictions of the NREL Phase VI rotor in the NASA Ames 80-by-120 wind tunnel［J］.Wind Energy，2002，5:151-169.

［7］BENJANIRAT S，SANKAR L N.Evaluation of turbulence models for the prediction of wind turbine aerodynamics［R］.AIAA 2003-0517，2003.

［8］EARL P N.DUQUE，BURKLUND M D.Navier-Stokes and comprehensive analysis performance predictions of the NREL Phase VI experiment［R］.AIAA 2003-0355，2003.

［9］SCHMITZ S，CHATTOT Jean-Jacques.Wind turbine blade aerodynamics of the NREL phase VI rotor near peak power［R］.AIAA 2005-4850，2005.

［10］LANGTRY R B，GOLA J，MENTER F R.Predicting 2D airfoil and 3D wind turbine rotor performance using a transition model for general CFD codes［R］.AIAA-2006-395，2006.

［11］MENTER F R，LANGTRY R，VOLKER S.Transition modelling for general purpose CFD codes［J］.Flow Turbulence Combust，2006，77:277-303.

［12］RAMSAY R R，HOFFMANN M J，GREGOREK G M，et al.Effects of grit roughness and pitch oscillations on the S809 airfoil［R］.Colorado:National Renewable Energy Laboratory，1995.