時域模態參數識別在南京長江大橋安全監測中的應用

郭 鑫,黃方林

(湖南省交通規劃勘察設計院,湖南長沙 410008)

0 引言

南京長江大橋是我國自行設計建造的首座特大鐵路、公路兩用鋼桁梁橋。江面正橋1 576 m。該橋位于我國鐵路南北通道京滬干線和公路干線寧楊國道上,是我國華東地區乃至全國發展國民經濟的重要交通命脈。全橋于1968年底通車,至今已經安全運營了42 a,但某些部位已經出現輕微病害。即將建立的南京長江大橋安全監測與狀態評估監測系統,將對橋梁的結構響應與行為以及橋梁工作環境進行實時監測,并利用獲取的信息分析結構的健康狀態、評估結構的可靠性,為橋梁管理與維護提供科學的決策依據。橋梁安全監測和狀態評估系統作為一多學科交叉的綜合體系,其理論覆蓋到振動理論、測試技術、系統辨識理論、信號分析與處理技術、計算機技術、可靠度等多門學科。從國內外應用的實例來看,目前普遍采用實驗模態分析方法來進行結構安全監測和狀態評估,因為它具有較好的在線性、遙感性和提取信號的方便性,而且由實測數據經分析得到的模態參數,像固有頻率、阻尼比、振型等都是反映結構整體性能的可靠“指紋”,可作為評價大橋整體性能的重要依據之一[1]。模態參數識別的方法有頻域法和時域法,其中頻域法相對較成熟,是模態參數識別的主要方法,常見的頻域法有半功率帶寬法、峰值法、導納圓法等方法[2]。但它的實驗設備較復雜,試驗周期也較長,特別是在對大型結構中的激振力無法測量時,用時域法進行模態參數識別的優點明顯。時域識別的方法很多,常用的有復指數法、對數衰減率法、ITD法[3]、STD法[4]、隨機減量法[5,6]等。本文介紹的是一種時域識別方法——逐步擴階雙遞推法[2]。逐步擴階雙遞推法是利用自由振動響應(或脈沖響應函數)識別系統復模態參數的時域參數識別法,它可克服復指數法判階困難的缺點。此外為了節省計算機機時和內存,采用了最小二乘遞推和逐步擴階的雙遞推法,提高了識別效率和精度。利用該法進行仿真計算和對南京橋實測數據分析,結果是令人滿意的。

1 理論背景

式中[M]、[C]、[K]分別為系統質量矩陣、阻尼矩陣、剛度矩陣,{x}、?x、 {??x}分別為用物理坐標描述的位移列陣、速度列陣、加速度列陣。考慮第k個測量點,它的自由響應表達式可表為:

一N自由度線性系統自由振動微分方程:

現以采樣周期Ts對xk(t)進行采樣,記tj=jTs,簡記為j(j=0,1,2,…),zi=eλiTs,則有:

式c1,c2,…,c2N為自回歸系數。以zj代替式(2)中系數矩陣相應行列式的第一列xk(j)(j=0,1,…,2N),則當z=zi時,行列式的第一列與i+1列成比例,式(3)仍成立,故得:

將式(4)時延得最小二乘解:

式中θr=(c1,c2,…,c2N)T;Rr=(-xk(1,0),-xk(2,0),…,-xk(r,0))T;Φr為θr的系數矩陣。求得c1,c2,…,c2N,解式(4),可得zi及復頻率λi。

利用一個測量點的自由振動響應數據,且作時延,構成Φr、Rr。式(5)中的Φr、Rr均為r行,用r行(即r個方程)由該式獲得的解記為θr、Φr、Rr,每增加一行(即增加一個方程),分別記為0),則可利用θr、及0)導得θr+1的最小二乘遞推公式:

其中初始值P0、θ0,在此可直接令P0=c2I,θ0=0,是計算機允許的充分大的數。

為了考慮測量噪聲的影響,讓噪聲模態有出口,假定響應中包含了N階復模態。利用低階的估計值θ,用遞推算法求得擴階后的θ*。令:

則與Φr相應的矩陣記為:

高校圖書館作為學術科研獲取信息資源的重要渠道，致力于OA學術資源的收錄、揭示、組織、管理等方面的研究與實踐，基本形成了資源收錄類型全、學科范圍廣、質量水平高、揭示角度多、揭示方式明確、組織方式科學、宣傳渠道多樣的整體局面，OA學術資源得到了較為廣泛的利用與傳播。

式中Φ1即為式(5)中模型階為i時的Φr。于是有:

解上式得:

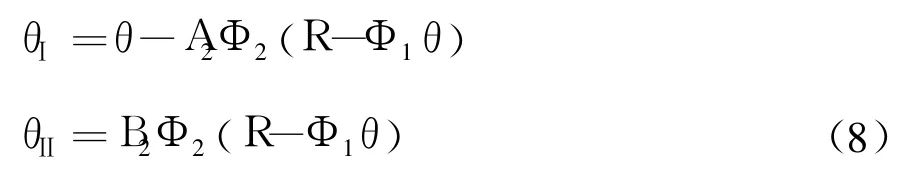
式中:

由式(8)可知,可根據i階模型的估計值θ,以及Φ1,Φ2,R可迅速算得擴階后得估計值θⅠ、θⅡ。矩陣B2的求逆僅僅是一個二階矩陣的求逆,比較方便。而矩陣C2的求逆可采用分塊矩陣求逆法。于是,我們就得到了一組逐步擴階雙遞推公式(6)、式(9)。具體步驟是:首先任意確定一個較小的擬合模型階i,按式(6)進行最小二乘遞推,推到第r個方程時得估計值θr,如需進行擴階,這時令C2=Pr、θ=θr,按式(9)進行擴階遞推,如有必要可增加新的方程,利用式(6)進行遞推,這時式(9)中的Pr=Cr,θr={θⅠ:θⅡ}T。由此可知,最小二乘遞推與逐步擴階遞推的組合,提供了方便、靈活的參數識別手段。

逐步擴階雙遞推法是利用自由振動響應(或脈沖響應函數)識別系統復模態參數。如果得到的數據是平穩隨機響應(如地脈動響應),可以通過隨機減量法[2]從線性振動系統的一個或多個平穩隨機響應樣本函數獲得該系統自由振動響應的數據。

2 仿真計算及實測結果驗證

2.1 仿真計算

考慮一個4自由度系統,其測量點1的自由響應為:

式中:

ω1=10 rad/s;ω2=40 rad/s;ω3=90 rad/s;ω4=160 rad/s;σ1=σ2=σ3=σ4=1.00;Ψ=[1 2 3 4]T。

為模擬測量噪聲,在x1(t)中分別添加10%,15%,20%的隨機白噪聲,用逐步擴階雙遞推最小二乘法進行識別,其結果見表1。

表1 仿真結果比較

仿真結果表明,在噪聲水平越低的情況下,識別模態參數精度越高。ψ中數值越大,對應階次的模態參數識別結果越好。

2.2 實測結果分析

利用CA—YD型加速度傳感器、DH5935放大器和便攜式計算機對南京長江大橋的響應進行了測量。測點主要布置在南京聯的主桁桿件、縱梁和橫梁上,采樣頻率為500Hz,記錄了大橋在上、下行各種客、貨列車通過時和無列車通過時的加速度響應。實測的南京聯中跨中截面的下弦桿豎向加速度響應(包括低通濾波后)及其自功率譜如圖1所示。

現截取一個測點的列車通過后余振數據,其豎向加速度響應(包括低通濾波后)及自功率譜如圖2～圖5所示。

圖1 實測大橋的加速度響應和頻譜曲線

圖2 濾波前的測點余振響應

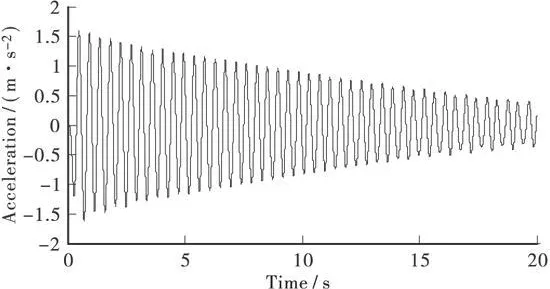
圖3 濾波后的測點余振響應

圖4 低通濾波前功率譜圖

圖5 低通濾波后功率譜圖

通過逐步擴階雙遞推最小二乘法計算得到結果:

1)濾波前得到固有頻率:2.225、4.679 4、5.388、9.941 3 Hz,對應阻尼比分別是:0.007 1、0.003 0、0.006 5、0.006 6。

2)低通濾波后得到固有頻率:2.230 3 Hz,阻尼比:0.013 6。

通過ANSYS軟件對南京橋動態分析得到的前10階固有頻率如表2所示。可知余振響應中第二階模態占主要成分。

表2 理論計算的前10階固有頻率

3 結論

模態參數作為反映整體結構動力特性的可靠“指紋”,在大型復雜結構的安全監測中起著重要的作用。為識別南京長江大橋模態參數,且不影響其正常運營,時域識別是非常適用的。

本文介紹的逐步擴階雙遞推最小二乘法及其與隨機減量法的綜合運用可對火車過橋、過橋后的余振、地脈動等各種情況下由測量到的響應進行模態參數識別。仿真與實測數據分析結果表明該方法應用于南京長江大橋安全監測是可行的。

[1]何旭輝,陳政清,黃方林.南京長江大橋安全監測和狀態評估的初步研究[Z].

[2]周傳榮,趙淳生.機械振動參數識別及其應用[M].北京:科學出版社,1989.

[3]Ibrahim SR,Mikulcik EC.Amethod for the direct identification of vibration[J].Shocked Vibration Bulletin,Part 4,1997.

[4]Ibrahim SR.An approach for reducing computational requirements in modal identification[J].AIAA Journal,1986,24(10).

[5]Ibrahim SR.Random decrement technique formodal identification of structures[J].J.of Spacecraft and Rockets,1977,14(11).

[6]黃方林,何旭輝,陳政清,等.隨機減量法在斜拉橋拉索模態參數識別中的應用[J].機械強度,2002,24(3).

[7]Huang Fanglin,He Xunhui,et al.Health Monitoring for Nanjing Yangtse River Bridge[Z].Proc of the 7th Int.Symposium on structural Engr.for young experts,Tianjing,2002.

[8]劉君輝,宋友成.大跨度橋梁施工過程中參數識別的BP神經網絡方法[J].湖南交通科技,2003,29(2):49-51.

[9]虢曙安.連續剛構橋施工控制中的參數識別方法研究[J].公路工程,2009,34(3):135-137.

[10]郭木華.基于二分法的斜拉橋施工控制過程參數識別[J].公路工程,2010,35(3):132-135.

[11]張治國,張謝東.基于模態分析理論和神經網絡的斜拉橋拉索損傷識別研究[J].中南公路工程,2007,32(2):67-72.

[12]喻力斌.楊梅昌江大橋T梁安全架設方案的實施[J].中南公路工程,2005,30(2):130-131.