“分點線三角形面積定理”的另證

●顏美玲 (杭州外國語學校 浙江杭州 310023)

“分點線三角形面積定理”的另證

●顏美玲 (杭州外國語學校 浙江杭州 310023)

《數學通訊》2007年第23期刊登了題為《分點線三角形面積定理》一文［1］，其中介紹了分點線三角形的定義及面積的有關結論如下:

定義1三角形頂點及對邊分點的連線稱為三角形的分點線．

定義2由三角形的分點線圍成的三角形稱為分點線三角形．

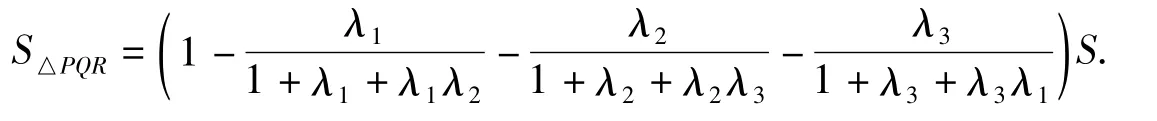
文獻［1］中添加了3條輔助線，利用面積之間的關系證明了上述定理．本文嘗試用復數法證明并得到了更優美的結論．

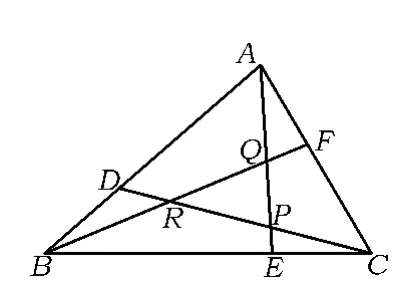
圖1

1 預備知識

1．1 三角形面積公式

如圖1，△ABC 的邊AB，BC，CA 上的分點分別為 D，E，F，AE 和CD，BF 和 AE，CD和BF分別交于點P，Q，R，則CD，BF，AE稱為△ABC的分點線，△PQR稱為△ABC的分點線三角形．

定理1設△ABC的面積為S，D，E，F分別是邊AB，BC，CA的分點，AE和CD，BF 和AE，CD 和BF 分別交于點P，Q，R，且AD ∶DB=λ1，BE ∶EC=λ2，CF ∶FA=λ3，則分點三角形△PQR的面積為

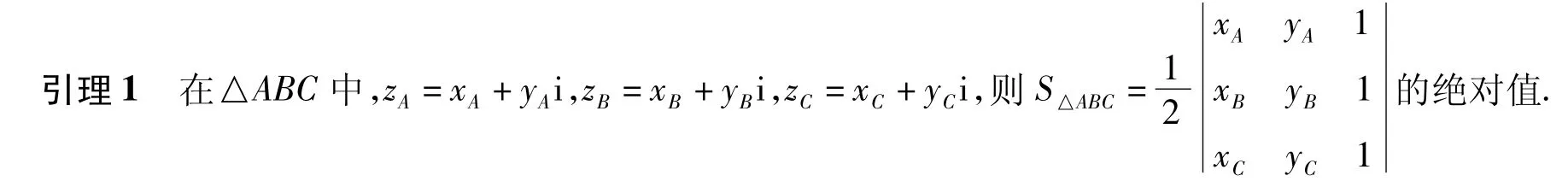
1．2 定比分點公式

2 復數法證明定理

證明如圖2，以B為原點，BC軸為實軸引進復平面，則

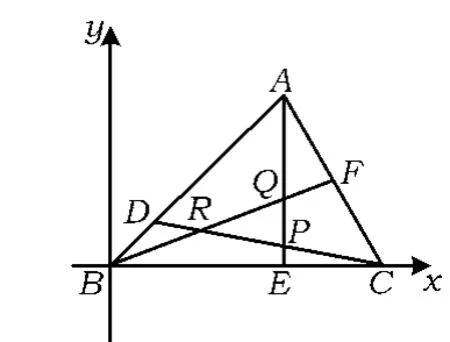
圖2

注2定理1中3個分點分別在3條邊上，如果3個分點在邊的延長線上呢?根據復數法的證明不難發現該方法對分點在邊延長線上也同樣適用．故結論可統一為:

定理2設△ABC的面積為S，D，E，F分別是AB，BC，CA的分點(分點在邊上或者在邊的延長線上)，直線 AE 和 CD，BF 和 AE，CD 和 BF 分別交于點 P，Q，R，且 AD ∶DB=λ1，BE ∶EC=λ2，CF ∶FA=λ，則

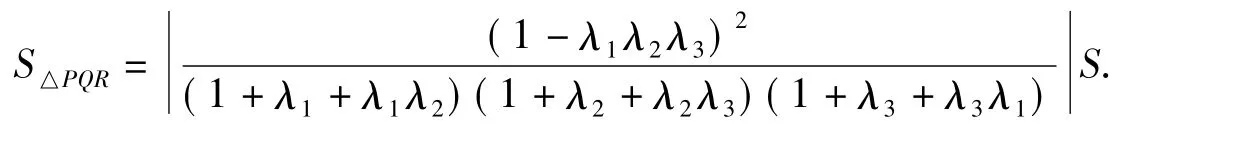
［1］ 張榮遠．分點線三角形面積定理［J］．數學通訊，2007(23):29-30．

［2］ 程其堅．怎樣用復數解題［M］．上海:上海教育出版社，1964．