與函數有關的高考試題分析

●錢建英 來國平 (長河高級中學 浙江杭州 310052)

與函數有關的高考試題分析

●錢建英 來國平 (長河高級中學 浙江杭州 310052)

1 考試要求

1．1 注重對函數基本知識的考查

主要考查函數的基本概念、基本性質和基本的計算、解題方法，多屬于函數部分的基本練習或課本上題目的變形與創新，體現高考數學試題源于課本的命題原則．

1．2 注重對函數主干知識的考查

為了突出函數在中學數學中的主線地位，在每年的新課程高考試題中，除考查純函數的知識外，函數方程的思想在其他試題中體現得淋漓盡致．

1．3 突出以函數為主的綜合應用

函數與方程、數列、不等式、導數、解析幾何、立體幾何等的相互滲透和交叉一直是高考的熱點，并且常考常新．

2 考點回顧

函數是高考數學中極為重要的內容．函數概念反映了現實世界中變量間的相互依存、相互制約的變化規律，函數的觀點和方法是高中數學研究的對象，同時本身就是數學中常用的一種思想方法，廣泛地滲透到高中數學學習的全過程及其他各學科中．同時函數又是學習高等數學的基礎，內容極為豐富．縱觀近幾年的高考試題發現，函數(不含三角函數)在選擇、填空、解答這3種題型中都有出現，占全卷的20%左右．既有容易題，又有中檔題與難題．近幾年的高考著重考查了二次函數(方程、零點)、分段函數、圖像與性質、函數的單調性、最值、導數的運算、導數的應用、不等式等重要知識，以及等價轉化、方程思想、數形結合、分類討論等重要的數學思想方法，對學生綜合運用所學知識分析和解決問題能力的要求較高．

3 命題熱點及生長點情況

近年來，有關函數內容的高考命題特點是:

(1)全方位:在近幾年的高考題中，函數的所有知識點都考過，雖然不強調知識點的覆蓋率，但每一年函數知識點的覆蓋率依然沒有減少．

(2)多層次:在每年的高考題中，低檔、中檔、高檔難度的函數題都有，且選擇、填空、解答題型齊全．低檔題一般僅涉及函數本身的內容，如定義域、值域、單調性、周期性、圖像、反函數(要求降低)，且對能力的要求不高;中、高檔題多為綜合程度較大的問題，或者是函數與其他知識結合，或者是多種方法的滲透．

(3)巧綜合:為了突出函數在中學中的重要地位，近幾年來高考強化了函數對其他知識的滲透，加大了以函數為載體的多種方法、多種能力的綜合程度，特別是函數、導數及其知識的綜合應用．

(4)變角度:出于“立意”和“創新”的需要，函數試題設置問題的角度和方式也不斷創新．重視函數思想的考查集中體現了函數與方程、數形結合、分類討論等的思想方法．函數的類型較多，概念、公式較多，具有較強的綜合性，從而使函數考題顯得新穎、生動、靈活．

4 典例剖析

4．1 函數在選擇題、填空題中的考查類型

(1)從函數的概念及性質出發．

評注本題主要考查了函數的概念、定義域、值域、圖像和對數函數的相關知識點，對數學素養有較高要求，體現了對能力的考查，屬中檔題．

(2)從函數的類型出發．

評注 本題主要考查對數的單調性、對數的基本運算及分類討論思想，屬中檔題．

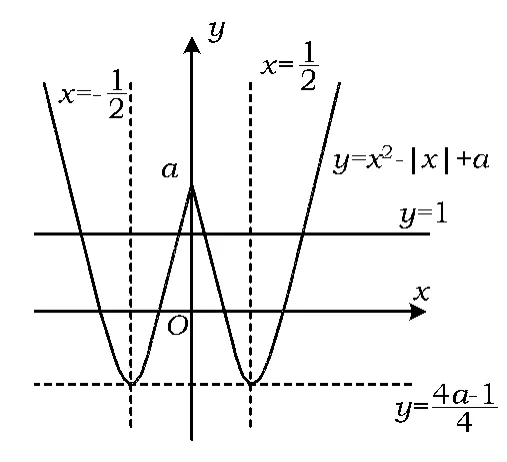
圖1

評注本題考查的是數形結合的思想方法．

4．2 函數在解答題中的考查類型

(1)函數與導數的結合，既求函數的極值與最值，又考查函數的單調性．

綜上所述，f(x)在區間( －1，1］和［7，+∞)上是增函數，在區間(1，3］和［3，7)上是減函數．

評注此題屬中檔題，主要考查了導數的幾何意義、用導數的知識求極值、函數的單調性．

(2)函數應用題與綜合應用題考查的是學生的建模能力．

例5如圖2，縣城A和B相距20 km，現計劃在兩縣城外以AB為直徑的半圓弧上選擇一點C建造垃圾處理廠，其對城市的影響度與所

選地點到城市的距離有關，對城A和城B的總影響度為城A與城B的影響度之和，記點C到城A的距離為x km，建在C處的垃圾處理廠對城A和城B的總影響度為y．統計調查表明:垃圾處理廠對城A的影響度與所選地點到城A的距離的平方成反比，比例系數為4;對城B的影響度與所選地點到城B的距離的平方成反比，比例系數為k．當垃圾處理廠建在的中點時，對城A和城B的總影響度為0．065．

(1)將y表示成x的函數．

圖2

(2009年山東省數學高考試題)

評注本題主要考查了函數在實際問題中的應用，運用待定系數法求解函數解析式的能力和運用換元法和基本不等式研究函數的單調性等問題．

(3)函數與不等式、數列、向量、解析幾何的綜合問題．

表1 x的取值情況表

評注此題是高檔題，主要考查函數、方程、不等式、導數及其應用等基礎知識;考查了分類討論的數學思想以及轉化應用的能力;考查了綜合運用所學知識分析問題、解決問題的能力．

精題集粹

1．定義在R上的函數f(x)滿足

③若奇函數 f(x)對定義域內任意 x都有f(x)=f(2－x)，則f(x)為周期函數．其中真命題是 ( )

A．①② B．①③ C．②③ D．②

3．設函數 f(x)=g(x)+x2，曲線 y=g(x)在點(1，g(1))處的切線方程為y=2x+1，則曲線y=f(x)在點(1，f(1))處切線的斜率為 ( )

(1)若函數f(x)的圖像過原點，且在原點處的切線斜率是－3，求a，b的值;

(2)若函數f(x)在區間(－1，1)上不單調，求a的取值范圍．

參考答案

1．C 3．C 3．A 4．D 5．8

6．解(1)由題意得

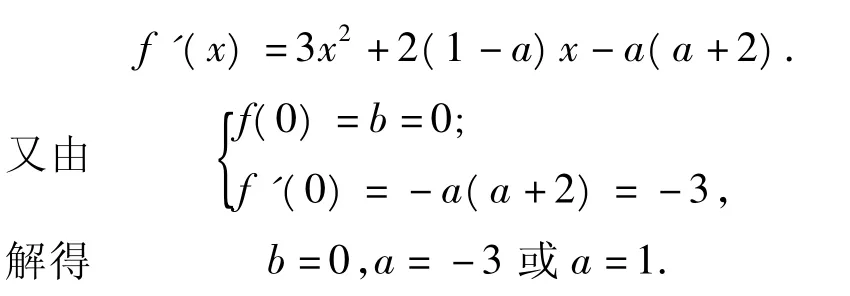
(2)函數f(x)在區間(－1，1)不單調，等價于導函數f'(x)在(－1，1)上既能取到大于0的實數，又能取到小于0的實數，即函數f'(x)在(－1，1)上存在零點．根據零點存在定理，有