對帶有非局部邊界條件的Dirac方程的跡的研究
梁銀雙,夏云青
(中州大學信息工程學院,鄭州450044)
右邊第二項的積分因單值性消失,則
3.csc(λ+m0)π的最簡分式展開式如下:
所以問題(I)的跡公式為
1引言
關于Sturm-Liouvile算子的跡的研究,已積累了大量文獻,不過大多數結果都是對局部方程局部邊界條件得到的。1981年李夢如教授在文獻[1]中得到下述帶有非局部邊界條件的S-L算子的跡公式:
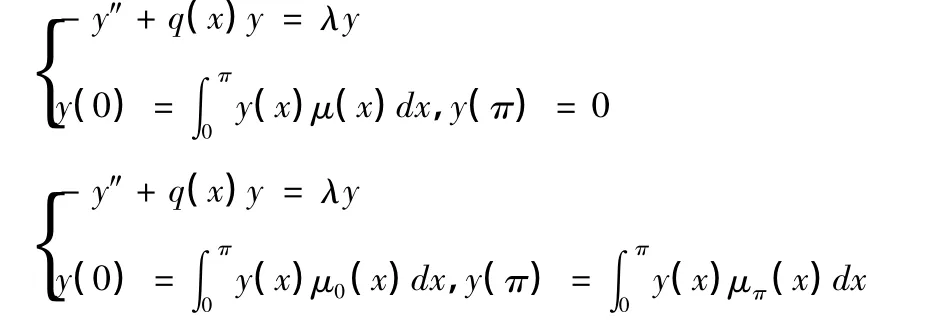
本篇論文主要研究下述問題漸近跡的公式:

p(x),r(x),μ(x) 均為[0,π]上的實值連續函數。
2問題(I)的整函數
我們先來考慮(I)的Cauchy問題(II):

引理1:由文獻[2]知:問題(II)的解φ(x,λ)對λ的漸近式為:
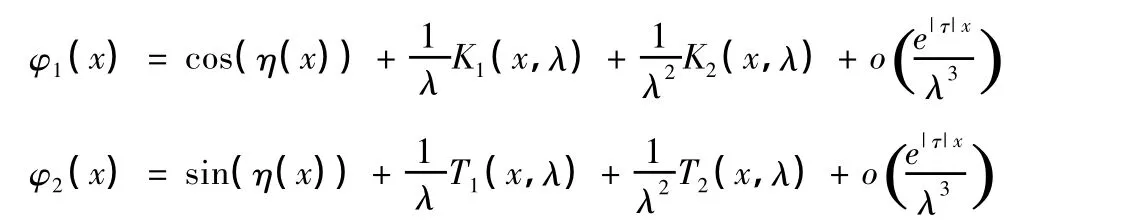
其中:

由此可知ω(λ)零點集合與(I)的特征值集合重合。下面計算整函數ω(λ)的漸近式。
由引理1知:
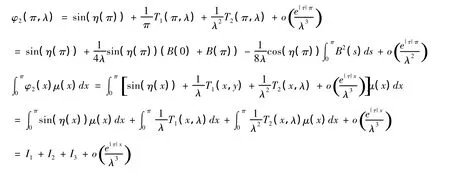
用分部積分可得:
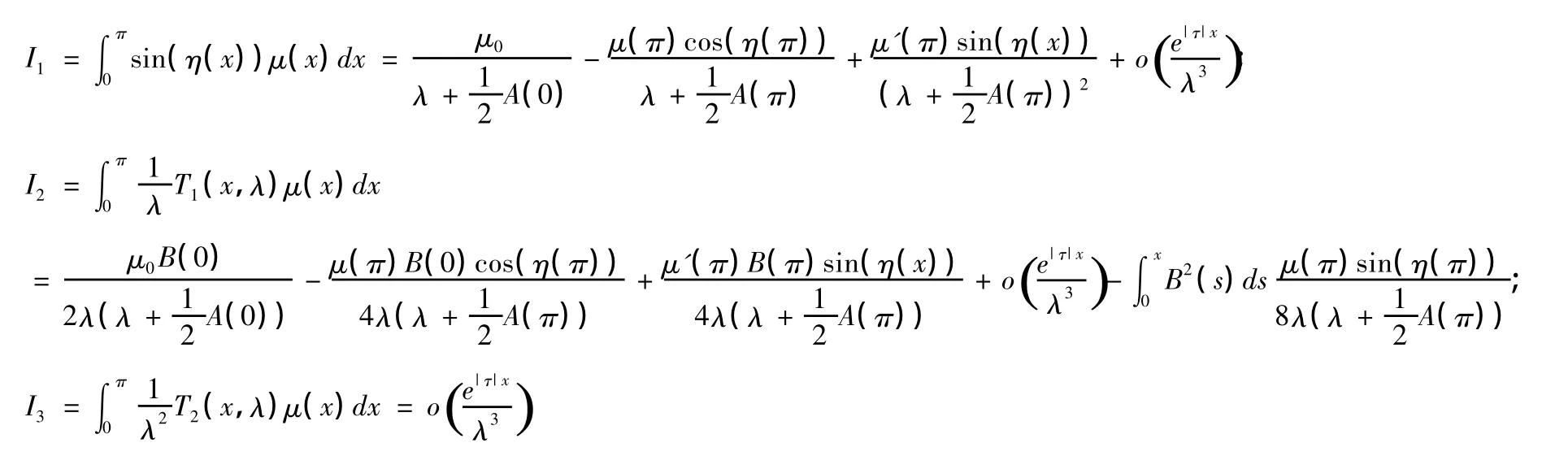
所以
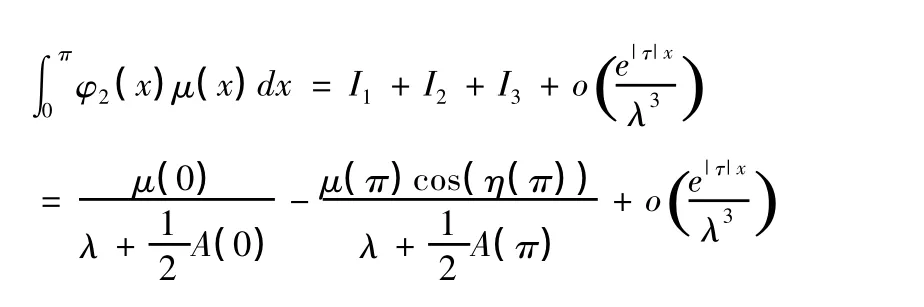
因而
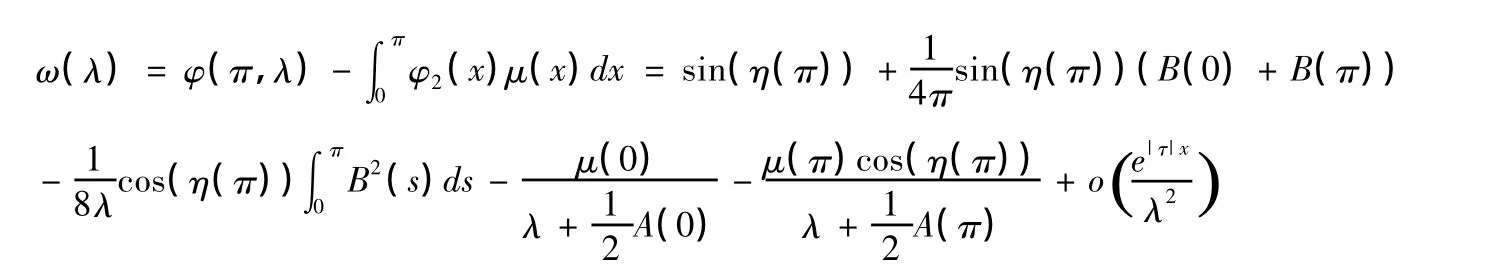
3問題(I)的跡
以下根據m0的不同取值來討論問題(I)的跡公式:
(1)若m0≠0,且m0不是整數
ω0(λ) 的零點為:λn=n - m0,n=0,± 1,±2,…
因此
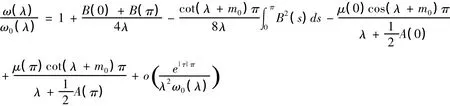
σ2= τ2=,在 CN上,以下三式均有界:
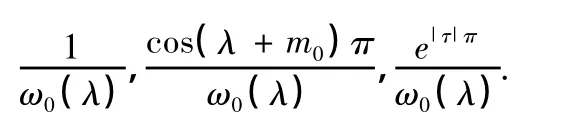
命題2:當N充分大時,ω(λ)與ω0(λ)在CN內有相同個數的零點。
證明:由引理2知:
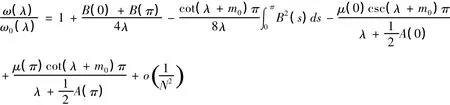
當 N充分大時,在Cn上有,因為ω(λ),ω0(λ)是λ的整函數,ω0(λ)在CN上無零點,由Rouche定理知,ω(λ)和ω0(λ)在CN內有相同個數的零點。
定理1:對于問題(I),設 p(x),r(x) ∈ C(2)[0,π],μ(x) ∈ C(3)[0,π],則有如下跡公式:
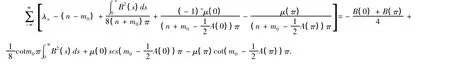
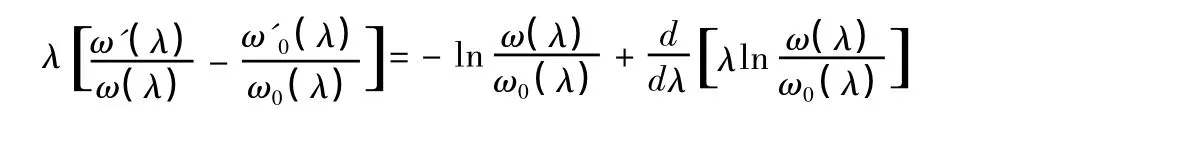
右邊第二項的積分因單值性消失,則
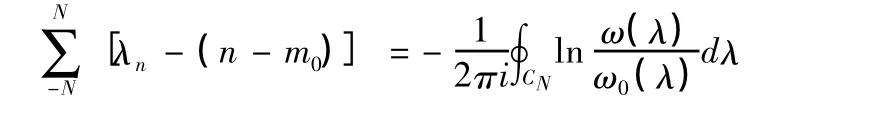
又
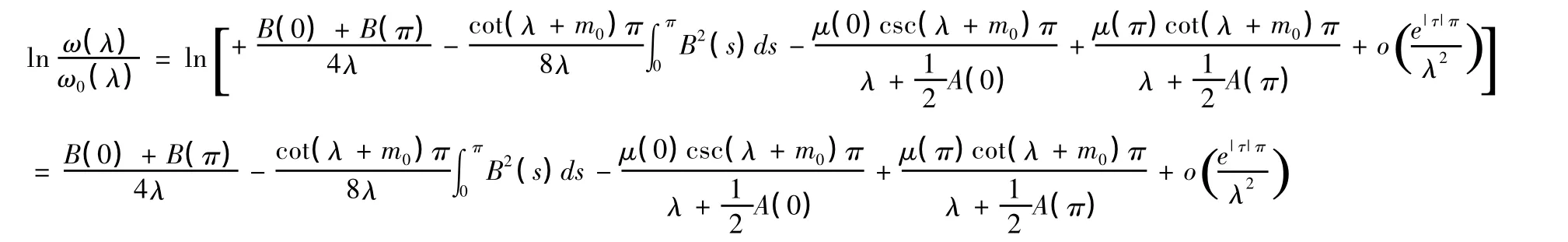
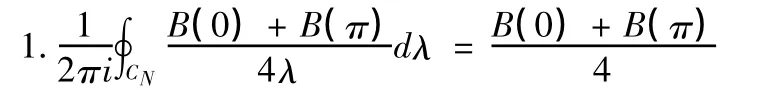
2.cot(λ+m0)π的最簡分式展開式如下:
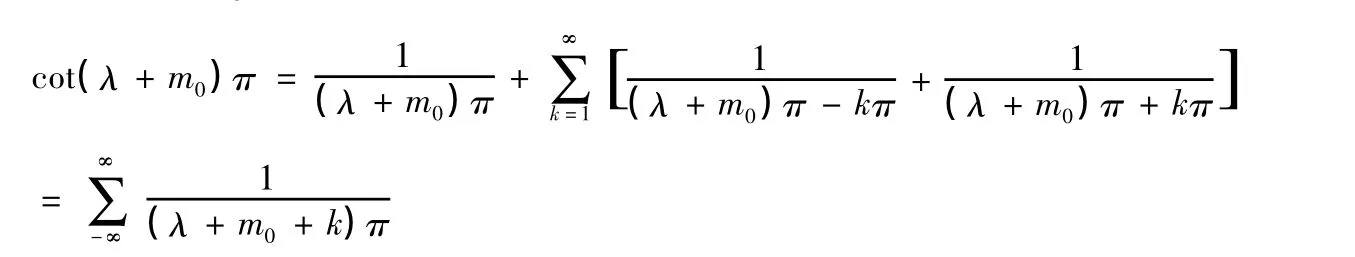
所以
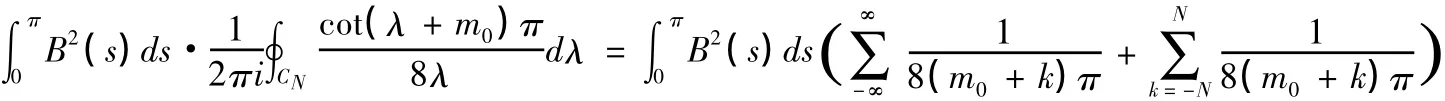
3.csc(λ+m0)π的最簡分式展開式如下:
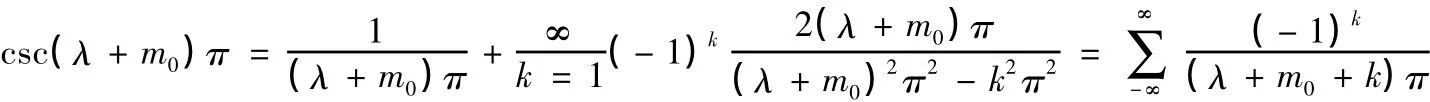
所以
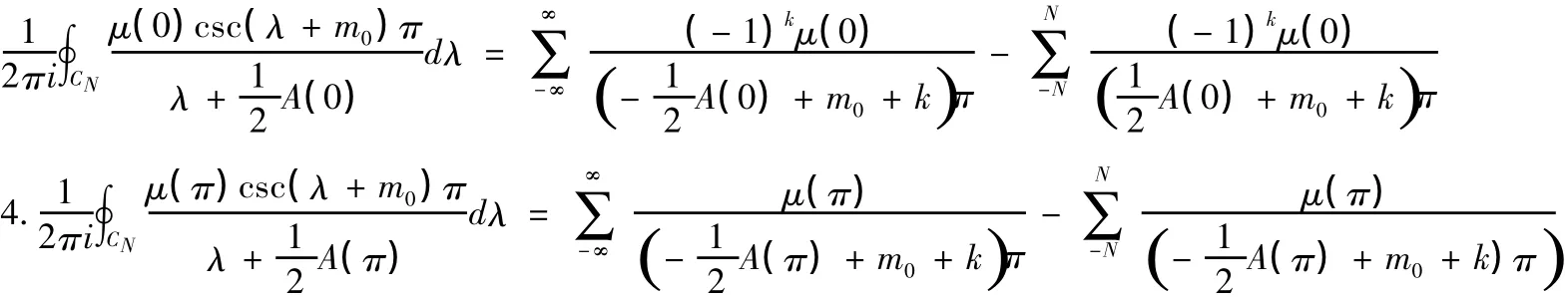
所以問題(I)的跡公式為
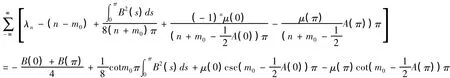
同理可得以下幾種情況的跡公式:(2)若m0=0,問題(I)的跡公式為
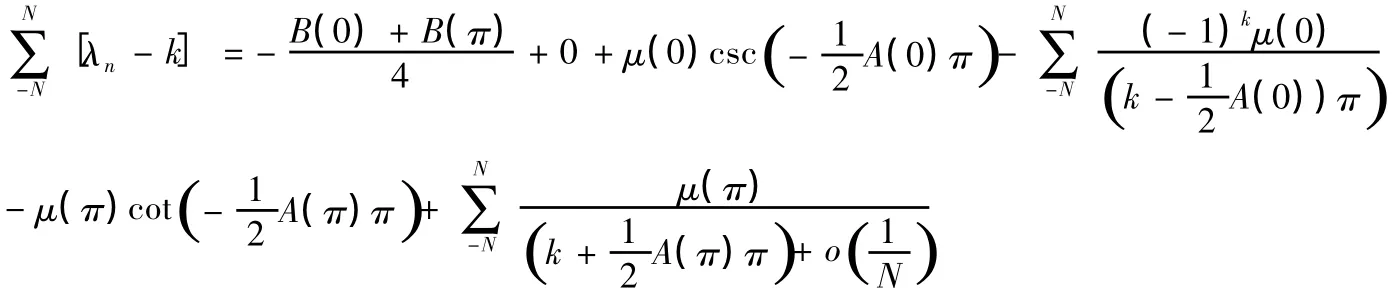
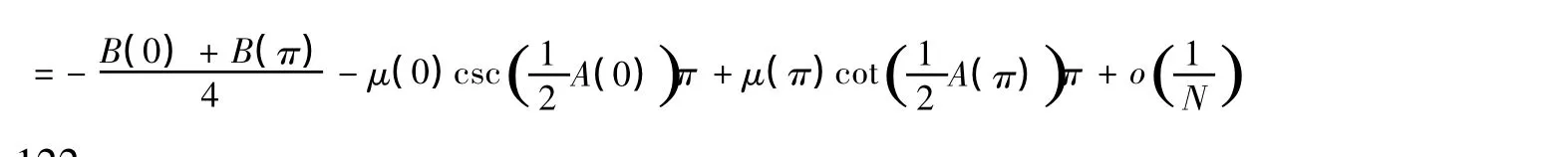
(3)m0≤Z且m0為偶數時,問題(1)的跡公式同m0=0的結果。
(4)m0∈Z且m0為奇數時,問題(1)的跡公式為:
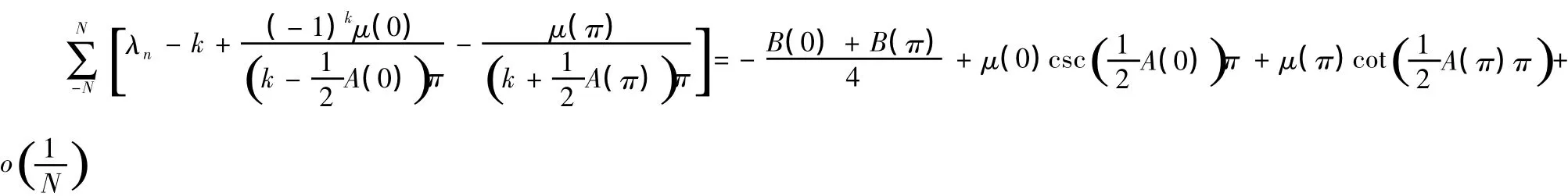
[1]李夢如.帶有非定局邊界條件的Sturm-Liouville算子的跡[J].鄭州大學學報:自然科學版,1981(1).
[2]Abdukadyrov E.Calculation of the regularized spur for the Dirac system[J].Journal of Moscow University,1967(4).
[3]曹策問.微分算子的跡[J].數學進展,1989,18(2):170 -178.
[4]曹策問.非自伴 Sturm -Liouville算子的漸近跡[J].數學學報,1981,24(1):84 -94.
[5]曹之江.常微分算子[M].上海:上海科技出版社,1985.
[6]Gelfand E M,Levitan B M.On trace identity for eigenvalue of differtial operator with sencod order[J].DAN,1953,88:593 -596.[7]Levitan B M,Sargsjan I S.Sturm - Liouville and Dirac operators[J].Kluwer Academic Publishers,1991(4).
[8]納依瑪克.線性微分算子[M].北京:科學出版社,1964.

