唐山市人口數值預測

武志勇,霍曉姝,劉家順

(河北理工大學經濟管理學院,河北唐山 063009)

唐山市人口數值預測

武志勇,霍曉姝,劉家順

(河北理工大學經濟管理學院,河北唐山 063009)

人口預測;馬爾薩斯人口模型;邏輯斯蒂人口模型

分析了 1978年以來唐山市人口發展的現狀,選擇唐山市 1978—2005年的總人口統計數據來建立馬爾薩斯人口模型和Logistic人口模型,并運用 2006—2007年的總人口數據來驗證模型,對唐山市未來 8年的總人口數進行了預測,以期對唐山市統籌人口發展提供借鑒。

人口問題已成為我國面臨的重要問題之一。唐山市正處在經濟快速增長的過程中,作為一個重工業城市,同時面臨人口、資源、環境與就業等問題的壓力。適度的人口規模是經濟、社會、資源和環境保護協調發展的強有力保證。認識人口數量的變化規律,建立人口模型,作出較準確的預報,是有效控制人口增長的前提。

18世紀末,英國人口學家馬爾薩斯對百余年的人口統計資料進行了研究,于 1798年提出人口指數增長模型。他的基本假設是:單位時間內人口的增長量與當時的人口總數成正比。但從長期來看,任何地區的人口都不可能無限增長,由于受到自然資源、環境條件等因素的影響,而當人口增加到一定數量以后,這個增長率就要隨著人口的增加而減少。為此,荷蘭生物數學家Verhulst在 19世紀中葉提出了阻滯增長模型,即邏輯斯蒂 (Logistic)模型。

一 唐山市總人口及其增長率的變化趨勢分析

從圖 1可以看出,唐山市總人口從 1978年的 558.47萬人增加到 2007年的 724.66萬人,30年時間增加了166.19萬人,平均年增長率為 7.17‰。

唐山市 1978年至今總人口數的變化趨勢主要表現為:總人口數逐年增長,年增長率的總的趨勢是高—低—高—更低,1978—1982年以及 1987—1990年進入高增長期,平均增長率達到 12.27‰;1983—1986年比較低,平均為7.65‰;1991年之后人口增長率處于更低水平,平均為4.35‰,且總體趨勢平穩,這一定程度上反映了唐山市計劃生育近些年取得了一定的成效。與此同時,我們還應看到:盡管近年來,唐山市人口增長速度較慢,但每年出生人口的絕對數仍然很大,未來相當一段時間內將是人口數量龐大和人口持續增長并存。

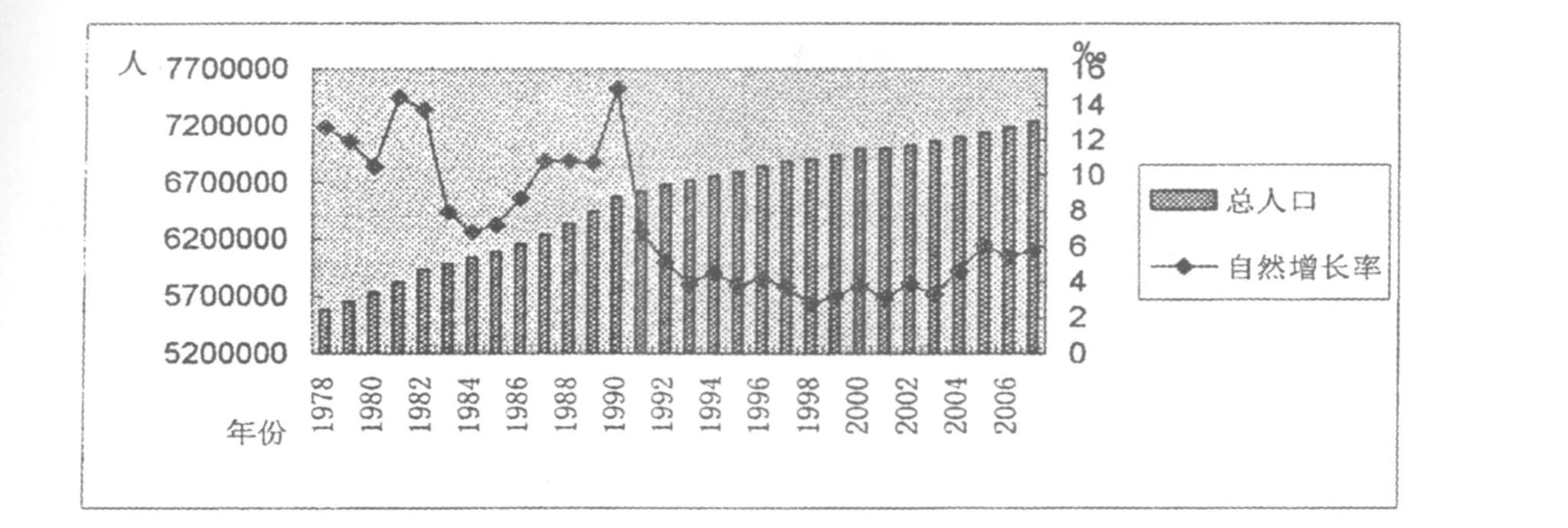
圖1 唐山市歷年人口數及增長率數據來源:2007年唐山市統計年鑒

二 模型預測

1978年之后我國計劃生育進入蓬勃發展時期,本文選擇唐山市 1978—2005年的人口統計數據來建立馬爾薩斯人口模型、阻滯增長模型,運用 2006—2007年的總人口數據來驗證模型,以此來預測唐山市未來 8年的總人口數。

1 馬爾薩斯人口模型

英國人口學家馬爾薩斯根據百余年的人口統計資料,提出了著名的基于指數增長的人口模型。該模型假設人口的增長率是常數。

我們可以近似地認為人口數 P(t)是時間變量 t的連續可微函數。以 r(t,p)表示人口出生率與死亡率之差,記為人口的凈增長率 (或叫做自然增長率),則有

假定凈增長率 r(t,p)為一常數,仍記為 r。并且在時刻 t0人口數為 p0,則得初值問題

解得它說明人口是依指數函數的規律增長的。這就是著名的馬爾薩斯人口論的數學模型。

唐山市 1978—2005年的年平均人口增長率為 7.28‰,但是考慮到近十幾年增長率趨于平穩,所以這里取 1991—2005年增長率為取值空間,認為 1991—2005年唐山市人口年均增長率保持現有水平 4.19‰不變,以 2005年為基準年,推斷出 2006、2007年人口數,以 2007年實際根據統計數據為基準年,運用馬爾薩斯人口模型,可以得到 2008～2015年唐山市總人口的預測數據,具體數據見表 1。

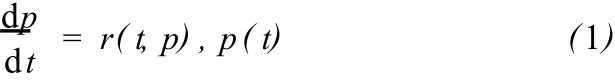
表 1 唐山市 2006—2015年人口預測 (單位:萬人)

由表中數據可以看到,“十一五”最后一年 2010年,總人口數達到 733.83萬,到“十二五”最后一年 2015年唐山市人口達到 749.36萬人。

2 邏輯斯蒂人口增長模型

由方程 (3)當 r＞0時人口數將無限增加,這顯然是不符合實際情況的。由于受到自然資源,食物、醫療衛生、環境等條件的限制,人口數的增加是不可能無限制的。因此,人們在馬爾薩斯律上又加了一個 “競爭項”—bp (t)2,于是有

其中 a＞0,b＞0都是常數,且數值很小。非線性方程 (4)稱為生物群體增長的邏輯率,a,b稱為生命系數。(4)是個變量可分離的方程,加上初始條件 p(t0) =p0,

顯然有

模型 (5)稱為 Logistic模型。利用導數做出函數 (5)的圖像,如圖 2所示它是一條“S”形曲線,可以看到:當總人口數未達到 a/2b時是加速增長時期,過了 a/2b后是減速增長時期,但增長率為正,隨時間的增加而減少,t→+∞,p′→0。

為了計算模型 (5)中的 a,b選擇 t0,t1,t2三年的數據 p0=p(t0),p1=p(t1),p2=p(t2),其中 t1-t0=t2-t1=T,代入模型 (5)有

圖 2 Logistic模型

解得

我們選擇 1991年、1997年、2003年間距相等的三個年份 p(1991) = 6 627 690,p(1997) =6 883 354,p(2003) =7 062 834,計算得 a=0.037 2,b=0.4×10-8。

將 a=0.0372,b=0.4×10-8代入 (5)得到唐山市人口增長的計算公式:

從上可知,唐山市的人口極限約為 a/b=930(萬)。并且由該公式預測出唐山市2006年到2014年的總人口數如表2:

表 2 唐山市 2006年到 2014年的總人口數預測表 (單位:萬人)

三模型的驗證及未來人口預測

將 2005年、2006年的人口預測值與實際統計值之間進行比較,由表 3可以看出,兩種模型的相對誤差都較小,且一正一負,故本文采用兩種預測的平均值作為 2008—2014年總人口數的最終預測結果。

表 3 2005、2006年的人口預測值與實際統計值 (單位:萬人)的誤差

對應計算數據其誤差情況如表 4,相對誤差相對更小,數據也更加精確。

表 4 2005、2006年的平均人口預測值與實際統計值(單位:萬人)的誤差

通過加權平均可以得到未來 8年中人口預測值,如圖 3所示,可以看到,唐山市人口規模呈現較穩定的增長趨勢,“十一五”最后一年 2010年,人口規模估計會達到 737.89萬,而到 “十二五”最后一年 2015年人口規模將達到758.84萬。

人口增長同時受諸多因素的影響,所以,任何一種模型都不可能精確無誤地預測,但本文認為其結果還是具有一定的參考價值。

圖3 唐山市人口數值預測

[1] 邵曉鋒,張克新 .黃岡市人口增長模型的研究 [J].數學的實踐與認識,2008,7(13).

[2] 李紹成 .我國人口增長的數學模型探討 [J].綿陽農專學報,1994,11(1).

[3] 何萬生,等 .數學模型與建模 [M].甘肅教育出版社, 2001.

[4] 唐山統計年鑒 [M].中國統計出版社,2008.

[5] 劉華中 .Logistic模型在人口預測中的應用 [J].江蘇石油化工學院學報,1998,10(1).

[6] 賈曉峰,等 .微積分與數學模型 [M].高等教育出版社, 1999.

Key words:population forecast;malthus population model;logistic population model

Abstract:The article analyzes present situation of Tangshan population development in 1978,chooses the total population statistical data of Tangshan in 1978～2005 year to establish theMalthuspopulation model and the Logistic population model,and tests the model by using 2006～2007 year total population data,it also carries on the forecast on next eight years in Tangshan,which would provide reference to overall plan population development in Tangshan.

Research on the Forecast of Population Value of Tangshan

WU Zhi-yong,HUO Xiao-shu,L IU Jia-shun
(College of Economics andManagement,Hebei Polytechnic University,Tangshan Hebei 063009,China)

C 923

A

1673-2804(2010)05-0019-03

2009-12-17