讓數(shù)學(xué)思想滋潤學(xué)生的心田

李　新

名師檔案

李新，1970年10月出生，中共黨員，中學(xué)高級教師，江蘇省小學(xué)數(shù)學(xué)特級教師，江蘇省教育系統(tǒng)先進(jìn)工作者，蘇州市名教師，吳江市實(shí)驗(yàn)小學(xué)副校長。

他多次參與或承擔(dān)蘇州市與江蘇省級的課題研究，論文在省、國家級刊物上發(fā)表或獲獎的有60多篇。承擔(dān)市、省、全國級的公開課20多次，獲省級評課一等獎，多次應(yīng)邀赴省外講學(xué)。受到好評。2008年暑期擔(dān)任教育部援助西藏中小學(xué)骨干教師培訓(xùn)班講課專家和中西部農(nóng)村中小學(xué)教師國家級遠(yuǎn)程培訓(xùn)主講專家，圓滿完成了任務(wù)。是九年義務(wù)教育課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書小學(xué)《數(shù)學(xué)》(江蘇教育版)教材的編委，全程參與1-12冊教材的編寫工作。熱忱培養(yǎng)青年教師。指導(dǎo)多名青年教師成長為吳江市、蘇州市的骨干教師。

【教學(xué)內(nèi)容】

蘇教版義務(wù)教育課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書《數(shù)學(xué)》六年級(上冊)第1頁例1，并完成“練一練”和練習(xí)一第1～5題。

【教學(xué)目標(biāo)】

1使學(xué)生經(jīng)歷探索運(yùn)用方程解決較復(fù)雜的實(shí)際問題的過程，能將實(shí)際問題抽象成數(shù)學(xué)表達(dá)，并建立形如ax±b=c的方程，進(jìn)而解決問題，初步體會建模思想。

2使學(xué)生經(jīng)歷探索運(yùn)用等式的性質(zhì)解形如ax±b=c的方程的過程，能將形如ax±b=c的方程逐步轉(zhuǎn)化成形如x=a凸的形式。初步體會化歸思想。

【教學(xué)過程】

一、引入

談話：西安是我國的一座歷史文化名城。那里名勝古跡眾多，其中就有聞名遐邇的大雁塔和小雁塔(用課件出示大雁塔和小雁塔的圖片)。這節(jié)課我們就先來研究與這兩座塔有關(guān)的數(shù)學(xué)問題(用課件出示例1的文字部分)。

二、探索

1找數(shù)量間的相等關(guān)系。

(指名讀題)

師：通過讀題。你知道大雁塔和小雁塔的高度之間有什么關(guān)系嗎?

生：大雁塔高64米。比小雁塔高度的2倍少22米。(教師用課件呈現(xiàn)“大雁塔的高度比小雁塔高度的2倍少22米”)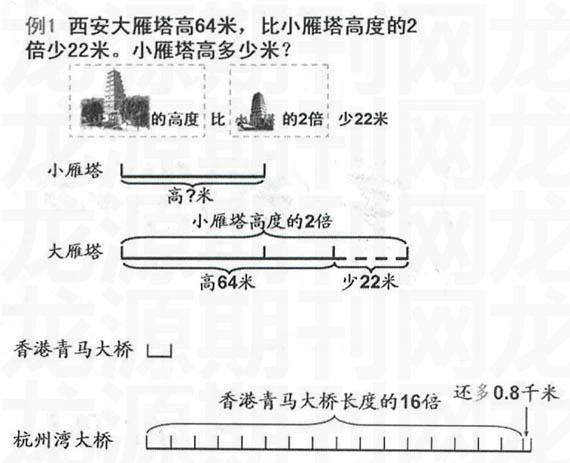

師：如果要用一幅線段圖來表示大雁塔和小雁塔高度之間的關(guān)系。可以怎樣畫?同桌討論一下。

生：我先畫一條線段表示小雁塔的高度。

師：為什么呢?

生：因?yàn)榭梢园研⊙闼母叨瓤醋?份，任意畫一條線段來表示，再畫表示大雁塔高度的線段。

師：(課件演示畫圖的部分過程：先畫一條線段，表示小雁塔的高度，再畫出小雁塔高度的2倍)你們能接著畫下去嗎?請看老師發(fā)給你們的練習(xí)紙，上面已經(jīng)畫好了和銀幕上一樣的圖。請根據(jù)“大雁塔的高度比小雁塔高度的2倍少22米”，接著畫下去。(學(xué)生畫圖，教師巡視)

師：(用實(shí)物投影展示一名學(xué)生畫的圖)你能說說為什么要這樣畫嗎?

生：(邊指圖邊說)這是小雁塔高度的2倍，大雁塔的高度比小雁塔高度的2倍少22米，所以從這里往回畫22米。

師：那么，哪一段表示了大雁塔的高度?

生：(指圖)從這里到這里。

師：和他一樣畫、一樣想的同學(xué)請舉手。(大多數(shù)學(xué)生舉手)

師：請大家看銀幕(銀幕上有如下內(nèi)容)，現(xiàn)在銀幕上有一個問題、一句話、一幅線段圖。根據(jù)這些內(nèi)容，你，能找出大雁塔與小雁塔高度之間的相等關(guān)系嗎?可以先在小組里討論一下。

生1：小雁塔的高度x2-22=大雁塔的高度。

師：(板書這一關(guān)系式)你是怎么想到這個關(guān)系式的?

生1：我是看著圖想的。

師：能說說想的過程嗎?

生1：我看到最下面的線段。“小雁塔高度的2倍”去掉“22米”就是“大雁塔的高度”。

生2：我是看著中間那句話來想的，因?yàn)椤按笱闼母叨缺刃⊙闼叨鹊?倍少22米”。所以就用“小雁塔高度的2倍”減“22米”等于“大雁塔的高度”。

師：兩位同學(xué)的想法都很好。請用其中一種想法再想一遍，并和同桌說一說想的過程。

師：大雁塔與小雁塔高度之間的這種相等關(guān)系。你還能用別的等式來表示嗎?

生：我用大雁塔的高度先加22再除以2。

師：(指線段圖)大家看，“‘大雁塔的高度+22”跟什么是相等的?

生：大雁塔的高度+22-小雁塔的高度×2。

師：(板書這個關(guān)系式)講得非常好!我們找到第二個等式來表示兩座塔高度之間的相等關(guān)系了。還能找到第三個嗎?(學(xué)生都不舉手，多數(shù)臉上有疑惑的表情)那么這樣，老師提示一下，這個等式的一邊是“22米”，大家想，另一邊可以寫上怎樣的式子，能和“22米”相等?

生：小雁塔的高度x2-大雁塔的高度=22。

師：誰能對照線段圖或這句關(guān)鍵的話。分析一下這個關(guān)系式是否正確?

生1：“大雁塔的高度”比“小雁塔高度的2倍”少，所以用“小雁塔高度的2倩”減“大雁塔的高度”。

生2：我看線段圖可以知道，“小雁塔高度的2倍”減“大雁塔的高度”等于22米。

2.列方程。

師：我們先看最先找到的關(guān)系式：小雁塔的高度x2-22=大雁塔的高度。在這個關(guān)系式中，已知“大雁塔的高度”是64米，求“小雁塔的高度”：像這樣的題，適合用什么方法解答?

生：用方程解。

師：怎樣設(shè)未知數(shù)呢?根據(jù)這個等量關(guān)系怎樣列方程呢?同桌討論一下。

生：設(shè)小雁塔高x米。2x-22=64。

師：這個方程的左邊表示什么?右邊呢?

生：左邊的“20x”表示“小雁塔高度的2倍”。減22米后就是“大雁塔的高度”；右邊是“大雁塔的高度”。

師：所以說這個方程左右兩邊表示了同一個數(shù)量。符合題意，是正確的。

3解方程。

師：這個方程和以前學(xué)過的方程有什么不同?

生：以前學(xué)過的方程左邊只有一步。這個方程左邊有兩步。

師：你能聯(lián)系實(shí)際問題，運(yùn)用以前學(xué)習(xí)的知識，想出解這個方程的第一步嗎?請動筆寫一寫。

(學(xué)生嘗試解方程，教師巡視指導(dǎo))

生1：2x-64+22。因?yàn)椤?x”是“小雁塔高度的2倍”。它就等于“大雁塔的高度”加“22米”。

生2：我也認(rèn)為2x=64+22。但我是這樣想的。方程的左邊要先算“2x”，就把“2x”當(dāng)作一個整體，這樣，方程的兩邊同時加22，就得到2x-64+22。

師：其實(shí)，×××(生1)的解法正好說明×××(生2)的解法是正確的。由于“小雁塔高度”未知。“小雁塔高度的2倍”也就未知，就可以把它看作一個整體。這樣。原來的方程就可以看作是“一個整體22=64”。就能運(yùn)用等式的性質(zhì)來解了。請大家把這種想法和同桌說一說，然后把這個方程繼續(xù)解完。

生：2x=86，x＝86÷2，x＝43。

師：這個方程的左邊有兩步，解這個方程時，最關(guān)鍵的步驟有哪些?

生：把2x看作一個整體，方程兩邊同時加22；方程變成2x=86后，兩邊再同時除以2。

師：大家看，方程兩邊同時加22后，方程左邊由兩步變成了一步；方程兩邊再同時除以2后，方程左邊只剩下x，右邊是43，就表示方程解完了。其實(shí)解方程的過程就是不斷運(yùn)用等式的性質(zhì)等知識，把原來比較復(fù)雜的

方程變得越來越簡單，一直簡單到“2x等于幾”的形式。

師：誰能檢驗(yàn)一下，結(jié)果是否正確?

生：把x＝43代入原方程。左邊=2x43-22=86-22＝64，右邊=64，左邊=右邊，所以x=43是原方程的解。

師：一開始我們檢驗(yàn)了所列的方程是正確的。現(xiàn)在檢驗(yàn)了結(jié)果也是正確的。所以，小雁塔高43米。

4小結(jié)。

師：誰能回顧一下，我們剛才用方程解決問題主要經(jīng)歷了哪些驟?

生1：先找到了大雁塔與小雁塔高度之間的相等關(guān)系。

生2：然后設(shè)未知數(shù)為x，并列出方程。

生3：再根據(jù)等式的性質(zhì)解方程，并檢驗(yàn)，最后寫出答案。

師：(結(jié)合學(xué)生口答，板書：找、設(shè)、列、解、驗(yàn)、答)你覺得這些步驟中。最關(guān)鍵的什么呢?

生：找數(shù)量問的相等關(guān)系。

5列不同的方程。

師：對這個問題，開始我們還寫出了另兩種關(guān)系式。請任意選一個關(guān)系式，也設(shè)小雁塔高x米，列出方程，并求出方程的解。

(生列方程、解方程)

生1：2x=-64+22，2x＝-86，x＝86÷2，x＝43。

生2：2x-64=22，2x=22+64，2x~=86，x=-86÷2，x=43。

師：觀察3個解方程的過程，有什么相同的地方?

生：都有2x=86這一步。

師：原來都是比較復(fù)雜的方程。運(yùn)用等式的性質(zhì)或經(jīng)過計(jì)算，都變成相同的簡單方程。所以說，3個方程雖然是依據(jù)不同的等量關(guān)系所列，但實(shí)質(zhì)上還是相同的。相比較而言，哪個方程所依據(jù)的等量關(guān)系思考時更順一些?

生：2x-22=64。

三、練習(xí)

1完成“練一練”。出示一幅線段圖：

師：能用一句話說明線段圖所表示的數(shù)量關(guān)系嗎?

生：杭州灣大橋全長比香港青馬大橋的16倍還多0.8千米。

師：杭州灣大橋已經(jīng)建成。它是目前世界上最長的跨海大橋，全長36千米。你能用方程求出香港青馬大橋的長度嗎?

(生解決問題)

生1：解：設(shè)香港青馬大橋長x千米。16x+0.8=36.16x=36-0.8，16x=35.2。x=2.2。

師：你根據(jù)什么等量關(guān)系列的方程?

生1：香港青馬大橋的長度×16+0.8=杭州灣大橋的長度。

師：誰能說說解這個方程，第一步可以怎樣想?

生2：把“16x”看作一個整體，方程兩邊同時減0.8。

師：結(jié)果是否正確，怎樣檢驗(yàn)?

生3：16×2.2+0.8=35.2+0.8=36。

師：這個“練一練”和例題有什么相同的地方?

生1：都要根據(jù)等量關(guān)系列出方程解答。

生2：列出的方程左邊都有兩步計(jì)算。

師：而且都是“幾x”加或減幾。那么解方程時有什么相同的地方?

生1：都要把“幾x”看作一個整體。

生2：都要兩次運(yùn)用等式的性質(zhì)。

2完成練習(xí)一第1題。

請學(xué)生看書上的題，獨(dú)立完成。教師巡視。請一位學(xué)生將解第(2)題“108+7x=3.9”的過程寫在黑板上，集體評講。

3完成練習(xí)一第2題。

請學(xué)生看書上的題，獨(dú)立完成第(1)題的填空，教師巡視，發(fā)現(xiàn)有些學(xué)生不會填。組織集體講評，課件逐步呈現(xiàn)如下內(nèi)容，指導(dǎo)學(xué)生思考。再讓學(xué)生獨(dú)立完成第(2)題，交流思考過程。

4完成練習(xí)一第3題。學(xué)生看書上的題，獨(dú)立完成。展示學(xué)生的作業(yè)，請學(xué)生說想的過程。

四、作業(yè)與總結(jié)(略)