小學(xué)數(shù)學(xué)綜合復(fù)習(xí)題解析例談

李曉明

新授課的側(cè)重點是知識的形成過程，而復(fù)習(xí)課的側(cè)重點應(yīng)該是培養(yǎng)學(xué)生運用知識解決問題的能力。所以復(fù)習(xí)課中的練習(xí)題必須有一定比例的綜合性練習(xí)題，讓學(xué)生通過練習(xí)對所學(xué)的知識能夠靈活運用，并進一步理解知識之間的聯(lián)系。這類題目一節(jié)課最多兩題為好。下面，我就結(jié)合一節(jié)復(fù)習(xí)課《圓的面積》談?wù)劸C合復(fù)習(xí)題的解析。

復(fù)習(xí)課上，當(dāng)我們復(fù)習(xí)梳理了《圓的面積》的重點知識，完成了基礎(chǔ)訓(xùn)練后，我出示了第一道綜合習(xí)題—“數(shù)學(xué)故事”： 很久以前，有一位英國女王歷盡艱辛來到一個非洲的部落，她向酋長要一塊土地。酋長不答應(yīng)，女王說：“我只要一塊牛皮那么大的土地。”酋長一聽，高興地說：“牛皮那么大的地才多大啊！送給你吧！” 聰明的女王用剪刀把牛皮剪成了細細的長條，并搓成了一條長1884米的繩子。原來，她要的是用牛皮繩圍成的土地。繩子搓好了，但是她應(yīng)該圍成一個正方形呢還是圍成一個圓好，你們幫她出出主意吧。

隨著這個問題的拋出，學(xué)生的思維活躍起來，有的說：“正方形的四個角是尖的，所以正方形面積大，圍成正方形。”也有的說：“圓的面積更大，應(yīng)該圍成圓形。”還有學(xué)生指出：“應(yīng)該計算一下它們的面積。”這時，我組織學(xué)生進行計算。通過計算，學(xué)生發(fā)現(xiàn)確實是圓的土地面積最大。這個結(jié)果讓學(xué)生興奮不已，竟然能解決這么復(fù)雜的問題！他們的自信心在不知不覺中得到了增強。筆者認(rèn)為，通過這樣的練習(xí)，不僅可以鞏固“已知正方形的周長求正方形的邊長，再利用邊長求面積”、“已知圓的周長求圓的半徑，再用半徑求面積”等所學(xué)知識，而且使學(xué)生體驗到了應(yīng)用數(shù)學(xué)知識解決實際問題的成就感。最重要的是通過這道題的解決，使學(xué)生意識到扎實地掌握基礎(chǔ)知識，提高自己綜合運用知識的能力的重要性。學(xué)生通過對這道習(xí)題的解決，還獲得了新的知識“周長相等的正方形和圓比較，圓的面積大。”這也是對所學(xué)知識的深化和升華。

在學(xué)生出色地解決了上面的習(xí)題后，我接著出示第二道習(xí)題：圓的周長是12.56厘米，圓的面積正好等于長方形OABC的面積，陰影部分的面積是多少平方厘米？

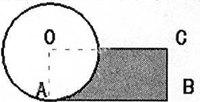
問題出示后，學(xué)生立即拿起筆計算起來。匯報的時候，學(xué)生中出現(xiàn)了不同的解法。

方法一：用圓的周長除以圓周率再除以2就得到半徑的長度，再利用半徑的長度求出圓的面積，然后用長方形的面積也就是圓的面積，減去四分之一圓的面積，最后就能得出陰影部分的面積。

方法二：因為圓的面積正好等于長方形OABC的面積，因此陰影部分的面積就是圓的面積減去四分之一圓的面積，也就是求出四分之三圓的面積就可以了。

顯然第二種方法較一要簡單一些。我請采用這種方法的學(xué)生上臺講解自己的思路，使其他學(xué)生也掌握了這種方法。

通過這道題的解析，不僅培養(yǎng)了學(xué)生綜合應(yīng)用知識的能力，最重要的使學(xué)生在交流與碰撞中思路大開，學(xué)會從不同的角度、用不同的方法分析思考同一問題，有助于發(fā)散思維能力的培養(yǎng)。同時，在比較中又優(yōu)化了計算的方法。

（責(zé)任編輯李 婧）