數學建模試題創編之初探

［摘 要］ 文章嘗試通過深入剖析數學建模的各個環節，探索高中數學建模試題的創編路徑. 該過程緊密依托教材內容，貼近生活實際，嚴格遵循數學教模的命題原則與評價機制. 同時，文章創新性地引入了多樣化的題型設計，包括填空題、選擇題與簡答題，旨在全面而深入地考查學生的數學建模素養.

［關鍵詞］ 數學建模；試題創編；命題

作者簡介：陳駿 （1982—） ，本科學歷，中學高級教師，從事高中數學教學與研究工作.

引言

《普通高中數學課程標準（2017年版2020年修訂）》（下文簡稱新課標）將數學建模活動及數學探究活動設置為一條獨立且顯著的主線，充分體現了對數學建模的重視程度.滬教版新教材將數學建模內容獨立編纂成冊——必修第四冊［1］與選擇性必修第三冊［2］，兩冊教材一共收錄了20個建模案例. 包羅萬象的主題，教師和學生能夠根據自己的興趣與專長進行選擇. 獨立編纂成冊的數學建模教材，憑借它的相對系統性和完整性，可以幫助教師理解數學建模的意義和特點，逐步體會并形成數學建模的教學規范，從而更好地引導學生參與相應的數學建模活動，體驗數學建模的全過程，領悟數學建模的真諦［3］.

如何考查學生的數學建模素養呢？在2022年上海市高三數學適應性測試中，出現了一道別具一格的試題——“探討房屋出租方案的優化決策”. 在給定問題的情況下，要求學生分析相關因素、提出合理假設，并用數學語言給出理由. 本試題分別從數學建模的不同環節過程和不同能力水平，全面考查學生的核心素養. 同時，本試題是數學建模領域的一個里程碑，激發了廣大同仁對建模試題創編的熱情. 筆者將盡力以教材中的案例為藍本，初步探討數學建模試題的創編路徑和形式，旨在激發更多思考與討論，起到拋磚引玉的作用.

考查建模活動中的各個環節

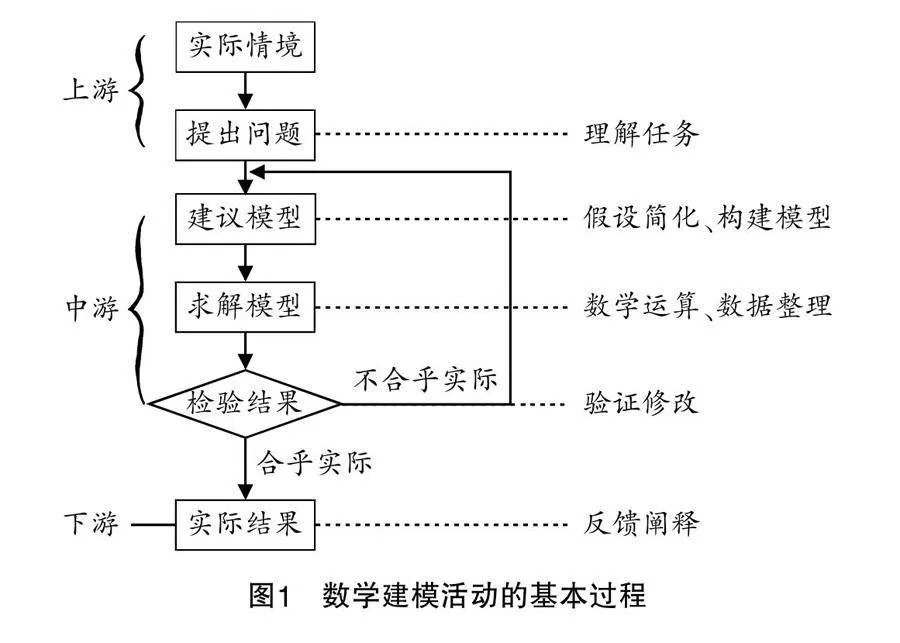
新課標給出了數學建模活動的基本過程，并指出“教學活動包括，對于給出的問題情境，經歷發現數學關聯、提出數學問題、構建數學模型、完善數學模型、得到數學結論、說明結論意義的全過程”［4］. 有學者將此過程分為上游、中游、下游三個階段［5］，筆者將兩者結合，得到如圖1所示的對應關系.

1. 提出問題環節

上游源于“在實際情境中從數學角度發現問題、提出問題”.試題中的問題，通常源于命題人的精心構思. 若鼓勵學生自主提出問題，不僅能夠深刻檢驗學生的分析與理解能力，更能反映學生的邏輯推理素養. 由于上游不涉及模型求解，復雜問題也能在此初步分析，故上游可考查的范圍較廣. 在此環節中，建議采用簡答題的形式來呈現所創編的試題.

例1 同學們如果時常閱讀報紙或瀏覽新聞網站，可能看到過關于大型車輛右轉時引發交通事故的報道.有時事故嚴重，危及了人的生命. 為什么大型車輛轉彎時容易引發事故？細讀一些報道和查閱相關資料后發現，這些事故中很大一部分與“內輪差”有關. 根據上述情境，請提出一個有意義的問題.（本題改編自必修第四冊《車輛轉彎時的安全隱患》）

參考答案 ①為什么“內輪差”會造成傷害事故？②產生“內輪差”的原因是什么？③“內輪差”的大小與哪些因素有關？

例2 同學們會利用假期游覽祖國大好河山，親身感受祖國在社會、經濟、文化等方面的發展.如果你有計劃去世界文化與自然雙重遺產之稱的黃山旅游，那么請你先制作一份游覽規劃吧！根據上述情境，請提出一個有意義的問題.（本題改編自必修第四冊《登山行程設計》）

參考答案 ①如何設計登山行程可以兼顧省時、省力、省錢的需求？②如何設計登山路線可以提高游玩的效率？

評析 上述兩題源于新教材中的案例，與日常生活息息相關，要求學生先用數學眼光觀察世界，理解事物的關聯，再用數學思維思考世界，提出明確的問題. 所謂“有意義的問題”是指值得去研究的問題，可以是現實問題，最好是數學化的問題. 提出一個有意義的問題是本環節的教學難點. 評價此類題目時，可按滿意原則打分.

2. 建立模型環節

中游的主要任務是建立、求解和檢驗模型，是數學建模的核心環節.學生需要注重知識儲備、經驗積累，更需要勇于探索的精神和攻堅克難的毅力，還需要一定的洞察力和想象力. 中游問題可以培養學生的創新精神，磨礪他們的意志，并充分反映他們的數學抽象、數學運算、數據分析等素養.

建立模型環節考查學生能否將現實模型轉化成數學模型，并提出合理的假設來簡化模型. 例如，《紅綠燈管理》案例中可以通過假設車流量均勻，忽略行人來簡化模型；《削菠蘿》案例中將菠蘿眼視作矩形內整齊排列的點陣. 事實上，基于不同的假設有可能得到不同的模型，假設的數量決定著后期求解模型的難易度. 在此環節中，建議采用簡答題或選擇題的形式呈現所創編的試題.

例3 在《雨中行》案例中，為使模型不至于太復雜，請你提出一個有效的假設.

參考答案 ①假設降雨強度保持不變；②將人體視為一個長方體；③假設行人的上半身保持固定的行走姿勢；④假設無風或者風向保持不變.

例4 在《雨中行》案例中，你認為下列哪些因素會對行人淋雨量的大小產生影響？（ ）

A. 風速？搖？搖 B. 風向？搖？搖

C. 降雨強度？搖？搖 D. 室外溫度

E. 行走速度

參考答案 ABCE

評析 上述兩題中，首先，學生要明確該案例的任務——減少在雨中行走時的淋雨量，即回溯上游；其次，考慮與該問題有關的因素和可以簡化模型的假設. 本環節的教學難點在于引導學生辨別各種因素的影響程度，既考驗學生對生活常識的積累，又考查學生的邏輯推理和數學抽象素養.

3. 求解模型環節

求解模型環節考查學生運用所學知識解決數學問題的能力. 學生需要根據具體情況綜合、靈活地運用幾何、代數、三角、統計等數學知識求解數學模型，需要平時的不斷積累和強化訓練. 此環節是現今數學建模過程中考查得最多的環節，即傳統的應用題，建議采用簡答題的形式呈現所創編的試題.例如，2017年高考上海卷第19題——共享單車保有量問題，2018年高考上海卷第19題——人均通勤時間問題，2021年上海卷第19題——企業營業額問題，等等，都以數學建模為載體，數學抽象在先，數學運算在中，邏輯推理在后，直觀想象在暗，綜合考查學生的數學學科核心素養.

4. 檢驗模型環節

檢驗模型環節考查學生能否將數學結果解釋為實際問題的結果或方案，并用實際的現象或數據加以驗證，通過反思模型的不足之處改進模型，從而培養學生的批判性思維. 在本環節中，建議采用填空題或簡答題的形式呈現所創編的試題.

例5 在《水葫蘆的生長》案例中，水葫蘆的生長規律需要按季節分成三段函數來擬合，因此二次函數模型并不能有效地刻畫水葫蘆的生長規律，則可采用______模型.

參考答案 邏輯斯蒂函數.

例6 小明將沙發通過轉角處的移動視為矩形在平面上的平移與旋轉運動，隨后建立相應的三角函數模型，最后算得矩形的較長邊大于轉角處的最大幅度，所以他判斷沙發無法通過該轉角. 而生活實際中，經驗豐富的搬運工卻能巧妙地通過. 你認為小明的建模方法不合理在哪里？應當如何改進？（本題改編自必修第四冊《家具搬運》）

參考答案 在家具搬運過程中，二維平面比三維空間的局限性大，可以考慮添加第三個維度或將沙發的最長邊豎起來搬運.

評析 本環節通過實際結果與模型結論的對比，讓學生找出模型不合理的原因，發現是由于因素考慮不全面，模型假設不合理，導致結論錯誤. 正確合理的數學模型通常不是一蹴而就就能建立的，對模型的檢驗和驗證必不可少，甚至需要多次反思和改進，最終達到理論與實踐的統一. 本環節對學生的觀察力和邏輯推理能力有較高要求，需要學生在日常生活中保持深入觀察和理性思考.

5. 反饋模型環節

下游的特點在于模型構建完成，主要考查模型的實際應用，既可以解釋模型，又可以闡釋結論. 例如，通過《“誘人”的優惠劵》案例可知，并不是物品買得越多，優惠率越高，所以提倡理性消費，制定一個合理的購物方案；通過《剎車距離》案例可知，反應時間是影響剎車距離的重要因素，因此駕車時須集中注意力，杜絕酒駕、疲勞駕駛，嚴格遵守交通規則. 即便是尚未學習過的復雜模型，也可以讓學生應用該模型解釋或解決實際問題，體現數學的應用價值和育人價值. 在本環節中，建議采用填空題或選擇題的形式呈現所創編的試題.

例7 （北京海淀區2021～2022學年高三上學期期中試題）某生物種群數量Q與時間t的關系近似地符合Q（t）=，給出下列四個結論：

①該生物種群的數量不會超過10；

②該生物種群數量的增長速度先逐漸變大后逐漸變小；

③該生物種群數量的增長速度與種群數量成正比；

④該生物種群數量的增長速度最大的時間t∈（2，3）.

依據上述關系式，其中所有正確結論的序號是________.

評析 本題中的關系式源于著名的邏輯斯蒂函數，該函數是描述在資源有限的條件下種群連續增長的一個最佳數學模型，稱為邏輯斯蒂增長. 這是在生物學中應用數學的經典范例，展現了數學的廣泛應用性. 高考數學中曾多次出現以該模型為背景的題目.即便學生沒有學過邏輯斯蒂函數，但依然可以利用該函數的運算結果，推理出各種結論. 本題主要考查學生的邏輯推理和數學運算素養.

結語

數學建模的試題創編可以針對建模過程中的各個環節，也可以針對數學建模的不同素養水平. 知識立足課本，內容貼近生活. 依據試題類型與評價形式的多樣性及靈活性進行編制，以更加契合數學教模的命題原則與評價機制. 上述內容是筆者對數學建模試題編制之若干見解的闡述. 數學建模試題編制工作尚處初探階段，諸多方面亟需深入探索與實踐，這需要廣大數學教育工作者夜以繼日地努力，共同推動試題質量與規模實現質的飛躍.

參考文獻：

［1］ 上海市中小學（幼兒園）課程改革委員會.普通高中數學必修第四冊［M］. 上海：上海教育出版社，2021.

［2］ 上海市中小學（幼兒園）課程改革委員會. 普通高中數學選擇性必修第三冊［M］. 上海：上海教育出版社，2021.

［3］ 上海市中小學（幼兒園）課程改革委員會. 普通高中數學教學參考資料必修第一冊［M］. 上海：上海教育出版社，2020.

［4］ 中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）［M］. 北京：人民教育出版社，2020.

［5］ 倪黎，茹凱，顏寶平. “數學建模”核心素養試題分析與命題探索［J］. 數學教育學報，2022，31（2）：69-76.