2024年高考數學新課標Ⅱ卷試題評價與教學建議

關鍵詞：高考數學；新課標Ⅱ卷；試題評價；教學建議

中圖分類號：G623.56 文獻標識碼：B 文章編號：1673-4289（2024）12-0048-04

一、2024年高考數學新課標Ⅱ卷試題評價

2024年全國高考數學新課標Ⅱ卷（以下簡稱“Ⅱ卷”）試題全面落實《中國高考評價體系》《普通高中數學課程標準（2017年版）》等文件精神，堅持立德樹人原則，改革試卷結構，突出拔尖創新人才選拔。Ⅱ卷有以下特點：①減少題量（首次采用全卷19個題），增加思維量；②基礎性試題比重較大（約60分左右），意在重視考查數學“四基”；③綜合性和應用性試題較多，意在全面考查數學“四能”和數學思想方法；④創新性試題增多，意在考查數學創新能力，并有利于選拔拔尖創新人才；⑤思維性試題明顯增多，提倡為思維而教、為思維而學、為思維而考；⑥突出主干知識考查，如函數與導數約占21%，三角約占16%，排列組合與概率統計約占16%，解析幾何約占13%，立體幾何約占13%，數列約占9%，其他內容（包括集合、簡單邏輯知識、復數、平面向量等）約占12%;⑦試卷的基礎題、中檔題和創新題層次分明、比例合適、區分明顯；⑧反猜題押題、反機械刷題的效果良好，對中學數學教學有良好導向作用。

二、部分“亮題”評析

Ⅱ卷的亮題較多，下面僅對部分亮題做一些探究。

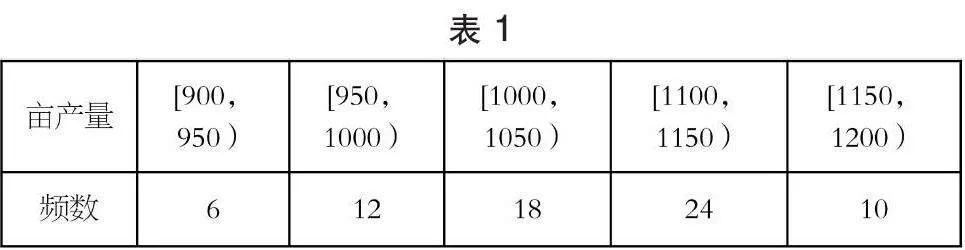
例1 （T4）某農業研究部門在面積相等的100塊稻田上種植一種新型水稻，得到各塊稻田的畝產量（單位：kg）并部分整理見表1。

根據表中數據，下列結論正確的是（ ）。

A.100塊稻田畝產量的中位數小于1050kg

B.100塊稻田中畝產量低于1100kg的稻田所占比例超過80%

C.100塊稻田畝產量的極差介于200kg至300kg之間

D.100塊稻田畝產量的平均值介于900kg至1000kg之間

評析：本題以二次曲線中帕斯卡定理（即二次曲線內接六邊形的其中兩組對邊分別平行，則第三組也相互平行）和遞推數列為背景，考查直線的斜率、雙曲線、等比數列、對稱點、面積等基礎知識，考查數學探究能力、數形結合思想、遞推思想、邏輯推理素養、運算素養和創新素養。

三、面向新高考的教學建議

（一）切實打好數學“四基”

數學“四基”是數學學習的基本目標，也是發展“四能”和生成數學核心素養的必要基礎。個體獲得“四基”的表征是：對數學基礎知識的理解，基本技能（方法）的熟練，基本思想的領悟，在此基礎上獲得具有意義和價值的數學信息即數學活動經驗。打好數學“四基”需要運用不同知識相對應的數學學習方式，即數學知識的學習靠理解，數學方法的掌握主要靠練習，數學思想的學習主要靠覺悟（感悟或領悟），數學經驗的獲得主要靠心力與心智協同操作的體驗。因此，打好數學“四基”的標志是理解數學知識、練習數學技能（方法）、感悟數學思想、積累數學經驗。數學“四基”的落腳點是數學經驗系統。在新課教學時，可經過“情境問題化、問題知識化、知識應用化、應用經驗化”等過程積累數學經驗；在復習教學時，應注意積累分析、探究、解決問題的經驗，也應注意積累數學創新的經驗。

（二）大力實施單元教學

單元教學是2017年版課標倡導的教學方式。單元教學能將零散、不成系統的知識“組織”起來，形成模塊化知識。單元教學把多個知識點集成為某個“單元”的教學，是一種“主題教學”，是學生形成知識模塊化的重要方法。單元教學具有主題明確、結構完整、聚焦問題、節省課時等特點。高考試題的綜合性表現為“知識點集成”，一般會在一道題目中涉及多個知識點及多種思想方法。如第4題考查中位數、極差、平均值等多個知識點；第9題考查三角函數的零點、最值、周期、對稱軸等多個知識點；第11題考查了三次函數的零點、極值、對稱軸、對稱中心等多個知識點。這種“知識點集成式”試題已是新高考命題的一大特色。其教學對策是，新課的章節復習和高三復習教學應以“主干知識模塊”“數學思想方法”“全息性高考真題”為單元或主題，以問題序列（串聯或并聯）為載體，以問題探究為教學范式，以培養和發展數學素養為目標，開展基于學情的單元教學。

（三）強化創新素養培養

逐步加強考查數學創新素養是新高考命題的新特點和新趨勢。對此，應實施數學創新教育和創新學習。學生的創新一般不是指狹義的原創，而是指廣義的創新，如學生提出一個新問題、猜想一個新命題、發現一種新解法、表達一個新觀點等都屬于創新，這些點滴、微小的創新（或改進）可稱為創新的星火，教師應善于點燃、呵護、累積創新的星火，使之逐漸成燎原之勢。創新教育需要時間，可多交度保障創新時間：一是把單元教學節約的時間用于數學探究和研究性學習；二是精選富有思維價值和探究價值的好問題（例題）；三是讓數學探究、研究性學習進入課堂，讓學習即研究成為課堂教學范式；四是鼓勵學生擠時間參加創新活動。實施數學創新教育應在健全創新人格、培養創新意識、學習創新思維、掌握創新方法、提高創新能力等方面下功夫。實施數學創新教育應重視采用知識發現教學法、問題探究教學法、猜想證明教學法、質疑批判教學法等方法。可在數學概念的產生與完善、數學命題的發現與推論、數學問題解決的思路探索與解題方法改進等過程中實施數學創新教育。