基于變異理論的教學(xué)素材設(shè)計(jì)模式

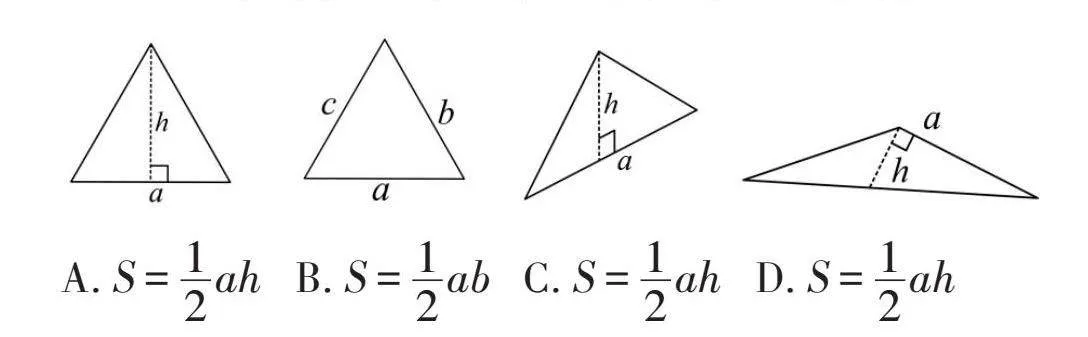
北京師范大學(xué)教育學(xué)部課程與教學(xué)研究院院長(zhǎng)，教授、博士生導(dǎo)師；中國(guó)教育學(xué)會(huì)小學(xué)數(shù)學(xué)教學(xué)專(zhuān)業(yè)委員會(huì)副秘書(shū)長(zhǎng)，中國(guó)教育發(fā)展戰(zhàn)略學(xué)會(huì)教育教學(xué)創(chuàng)新專(zhuān)業(yè)委員會(huì)副理事長(zhǎng)，中國(guó)少數(shù)民族教育學(xué)會(huì)數(shù)學(xué)教育專(zhuān)業(yè)委員會(huì)副理事長(zhǎng)；主持的課題有全國(guó)教育科學(xué)“十一五”規(guī)劃教育部重點(diǎn)課題“新課程小學(xué)數(shù)學(xué)、語(yǔ)文學(xué)科能力評(píng)價(jià)研究”、全國(guó)教育科學(xué)“十二五”規(guī)劃教育部重點(diǎn)課題“讀懂中小學(xué)生數(shù)學(xué)學(xué)習(xí)過(guò)程的方法研究”，以及國(guó)家自然科學(xué)基金面上項(xiàng)目“復(fù)雜情境下學(xué)生數(shù)學(xué)創(chuàng)造性思維的認(rèn)知及腦機(jī)制研究”等；著有《小學(xué)生數(shù)學(xué)能力評(píng)價(jià)研究》《小學(xué)數(shù)學(xué)互動(dòng)式教學(xué)》《學(xué)習(xí)者視角下的學(xué)習(xí)歷程分析》等專(zhuān)著，發(fā)表學(xué)術(shù)論文100余篇。

張春莉

變異理論是教學(xué)論專(zhuān)家、瑞典哥德堡大學(xué)教授馬飛龍（Ference Marton，又譯“馬騰”）創(chuàng)立的教學(xué)理論。該理論認(rèn)為，正是由于變異，我們才能審辨出學(xué)習(xí)內(nèi)容的關(guān)鍵屬性。基于變異理論的小學(xué)數(shù)學(xué)教學(xué)模式通過(guò)引入正反對(duì)比案例、多樣化的正例，為學(xué)生提供具有差異性和多樣性的信息，引導(dǎo)學(xué)生通過(guò)信息的對(duì)比、概括和融合，逐步聚焦概念的關(guān)鍵屬性，解決不同情境中的同類(lèi)問(wèn)題。這種教學(xué)模式有利于培養(yǎng)學(xué)生的批判性思維和問(wèn)題解決能力。本文在闡釋變異理論及其教學(xué)應(yīng)用的基礎(chǔ)上，以人教版數(shù)學(xué)五年級(jí)上冊(cè)“多邊形的面積”單元教學(xué)內(nèi)容為例，探析如何應(yīng)用變異理論設(shè)計(jì)”一題多變”教學(xué)素材，幫助學(xué)生掌握知識(shí)本質(zhì)，達(dá)到舉一反三、觸類(lèi)旁通的目的。

一、變異的三種模式

變異理論認(rèn)為，變異可分為對(duì)比、概括和融合三種模式。“對(duì)比”指在某個(gè)維度上比較兩個(gè)或多個(gè)事物、概念或現(xiàn)象之間的相似之處和差異之處。這種對(duì)比有利于突出事物的關(guān)鍵特征，使其更加明顯和清晰，有助于學(xué)生更好地認(rèn)識(shí)事物的本質(zhì)，加深對(duì)事物關(guān)鍵屬性的理解。這啟示教師，教學(xué)新內(nèi)容時(shí)可采取對(duì)比先行的教學(xué)原則。“概括”指在其他屬性變化的同時(shí)，保持某個(gè)關(guān)鍵屬性不變。這是一種逆向的教學(xué)設(shè)計(jì)思維，旨在引導(dǎo)學(xué)生在變化中找不變，進(jìn)而深刻地理解關(guān)鍵屬性。將不變作為背景，將變化的方面作為對(duì)象進(jìn)行考察，屬于對(duì)比模式；將變化作為背景，將不變的方面作為對(duì)象進(jìn)行考察，則體現(xiàn)了概括模式（祝錢(qián)，《基于“變異理論”的初中化學(xué)解題教學(xué)實(shí)踐——以實(shí)驗(yàn)探究題為例》，《化學(xué)教學(xué)》2020年第4期）。“融合”指向多個(gè)維度的變化，要求學(xué)生辨認(rèn)并考慮這些維度之間的關(guān)系以及它們與學(xué)習(xí)內(nèi)容的關(guān)系。借助融合多個(gè)維度的變化的學(xué)習(xí)素材，學(xué)生能夠更全面地理解和運(yùn)用新知。

二、不同變異模式在課堂教學(xué)中的應(yīng)用

我們可以基于變異的三種模式將變異理論應(yīng)用于小學(xué)數(shù)學(xué)教學(xué)。其具體表現(xiàn)有如下三種。

一是基于對(duì)比模式的正例與反例呈現(xiàn)。在教學(xué)新知識(shí)時(shí)，教師應(yīng)為學(xué)生提供該知識(shí)點(diǎn)所對(duì)應(yīng)的正例和反例，使學(xué)生通過(guò)比較發(fā)現(xiàn)兩個(gè)例子的差異，進(jìn)而把握該知識(shí)點(diǎn)的關(guān)鍵特征。例如，教學(xué)“多邊形的面積”單元中《梯形的面積》時(shí)，教師可將一般的平行四邊形、菱形和普通四邊形作為梯形的反例，幫助學(xué)生快速找到梯形的關(guān)鍵屬性——僅有一組對(duì)邊平行。二是基于概括模式的多樣化正例呈現(xiàn)。在找到關(guān)鍵屬性之后，我們需要固定關(guān)鍵屬性，同時(shí)改變其他屬性。在《梯形的面積》教學(xué)的這一階段，教師可以呈現(xiàn)梯形平行的一組對(duì)邊分別是水平、豎直或傾斜的多樣化情況，也可以從其他屬性出發(fā)，如非平行對(duì)邊的傾斜方向相同或不同的情況，讓學(xué)生通過(guò)多個(gè)實(shí)例進(jìn)一步理解已經(jīng)發(fā)現(xiàn)的關(guān)鍵屬性。三是基于融合模式的更加多樣化的正例呈現(xiàn)。后續(xù)教學(xué)階段，教師可以同步變化剛剛談及的多個(gè)非關(guān)鍵屬性，呈現(xiàn)更加“不規(guī)則”的梯形，讓學(xué)生從多種變化中找到始終不變的本質(zhì)屬性，全面、深入地理解新知。

三、依據(jù)變異理論設(shè)計(jì)“一題多變”教學(xué)素材

探究多邊形的面積計(jì)算，不僅是為了解決實(shí)際問(wèn)題，還有利于增強(qiáng)學(xué)生的空間觀(guān)念和推理意識(shí)。教材中相關(guān)內(nèi)容的編排邏輯是：從長(zhǎng)方形的面積公式探究開(kāi)始，順次安排平行四邊形、三角形、梯形的面積公式探究。這種逐步推進(jìn)的方式有助于學(xué)生建構(gòu)多邊形面積計(jì)算的通理通法，形成整體認(rèn)知：先通過(guò)割補(bǔ)、拆分、拼接等方式將未知面積公式的圖形轉(zhuǎn)化為已知面積公式的圖形，再通過(guò)圖形之間的聯(lián)系推導(dǎo)出新圖形的面積公式。實(shí)際教學(xué)中，學(xué)生常常在圖形面積計(jì)算方面出錯(cuò)，而將變異理論引入教學(xué)是提升教學(xué)效果的有效策略。下面，筆者基于以下教學(xué)路徑，談變異理論指導(dǎo)下的教學(xué)素材設(shè)計(jì)。

1.平行四邊形面積的教學(xué)素材設(shè)計(jì)

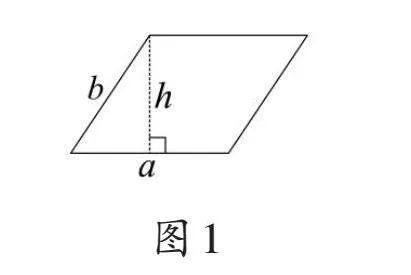
首先，教師應(yīng)采用對(duì)比的模式，通過(guò)提供清晰的正例和反例幫助學(xué)生理解平行四邊形面積計(jì)算的核心原則。如圖1所示，典型的正例可以是用底邊a和高？的乘積計(jì)算平行四邊形的面積，而反例要展示錯(cuò)誤做法，如誤認(rèn)為鄰邊a和b的乘積是面積。這是學(xué)生受長(zhǎng)方形面積公式影響而形成的常見(jiàn)誤區(qū)。學(xué)生結(jié)合長(zhǎng)方形面積計(jì)算的已有認(rèn)知，對(duì)比探析上述正例和反例，就可以明確二者的差異，辨明對(duì)錯(cuò)，進(jìn)而深入理解平行四邊形面積計(jì)算原理。

其次，在概括模式指導(dǎo)下的教學(xué)中，教師可引導(dǎo)學(xué)生從以下兩點(diǎn)出發(fā)，探析平行四邊形的面積計(jì)算方法，形成在不同情境中迅速應(yīng)用相關(guān)知識(shí)解決問(wèn)題的能力。

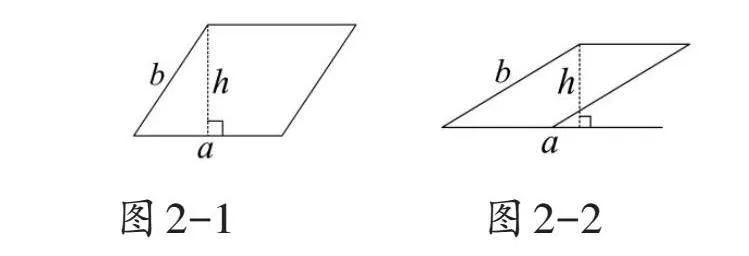
一是改變高的位置。如圖2所示，高無(wú)論是在平行四邊形內(nèi)部（圖2-1），還是在平行四邊形外部（圖2-2），教師都要引導(dǎo)學(xué)生發(fā)現(xiàn)水平底邊a這個(gè)“基準(zhǔn)”，從而正確“配對(duì)”底和高。

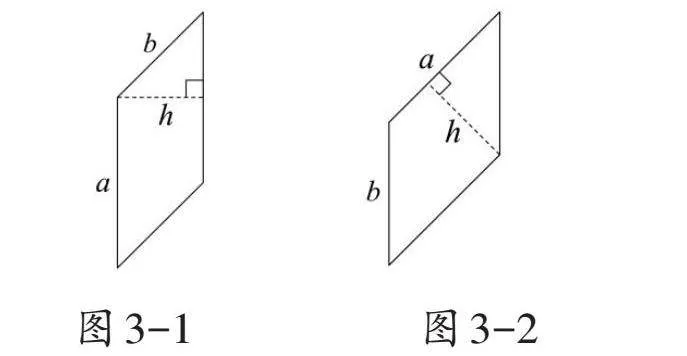
二是考慮底邊a的不同方向性。底邊a無(wú)論是水平、豎直（圖3-1）還是傾斜（圖3-2），教師都要引導(dǎo)學(xué)生找到相應(yīng)的高？，在正確“配對(duì)”的基礎(chǔ)上解決面積問(wèn)題。

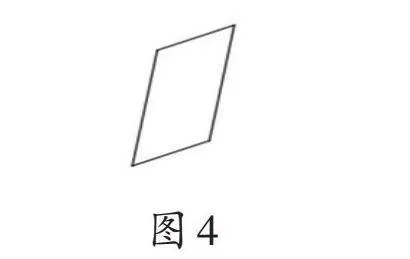
最終，在融合模式指導(dǎo)下，教師要通過(guò)提供具有多個(gè)變異維度的平行四邊形，引導(dǎo)學(xué)生計(jì)算面積并總結(jié)計(jì)算方法，形成更加全面的認(rèn)識(shí)。例如，求圖4所示平行四邊形面積的題目。

該平行四邊形的高需要學(xué)生自己尋找，邊長(zhǎng)需要學(xué)生自己測(cè)量，同時(shí)底邊是傾斜的，這體現(xiàn)了兩個(gè)維度上的變異。這種學(xué)習(xí)素材不僅有助于學(xué)生鞏固測(cè)量技能，還有助于學(xué)生加深對(duì)平行四邊形面積公式的理解，提高解決問(wèn)題的能力。

2.三角形面積和梯形面積的教學(xué)素材設(shè)計(jì)

參照以上變異模式，教師可以用相似的方式設(shè)計(jì)三角形、梯形面積教學(xué)。筆者以《三角形的面積》教學(xué)素材設(shè)計(jì)為例做具體闡述。

首先，教師基于對(duì)比模式設(shè)計(jì)并呈現(xiàn)正反兩種素材，引導(dǎo)學(xué)生精準(zhǔn)找到三角形的高，并合理運(yùn)用面積公式。教學(xué)素材如題目①。

①如圖，請(qǐng)?jiān)谙铝兴姆N求三角形面積的方法中，找出哪些方法是正確的，哪些方法是錯(cuò)誤的。

A.[S=12ah] B.[S=12ab] C.[S=12ah] D.[S=12ah]

然后，教師基于概括模式，確立三種變化屬性：改變?nèi)切蔚男螤睢尸F(xiàn)直角三角形、鈍角三角形、銳角三角形三種情況；改變底邊與水平面的關(guān)系——將作高的底邊傾斜，使之不與水平面平行；改變作高的頂點(diǎn)——過(guò)不同頂點(diǎn)作高，再求面積。這三種變化屬性分別對(duì)應(yīng)的教學(xué)素材是題目②③④。

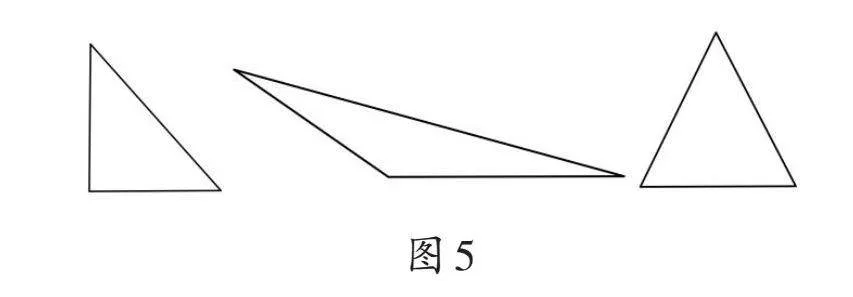
②測(cè)量圖5中三個(gè)三角形的邊長(zhǎng)并求出其面積。其中，第一個(gè)三角形為直角三角形。

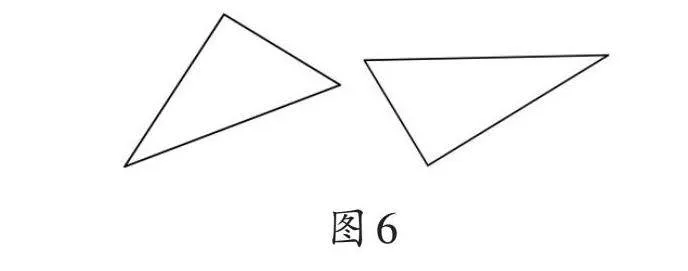
③測(cè)量圖6中兩個(gè)三角形的邊長(zhǎng)并求出其面積。

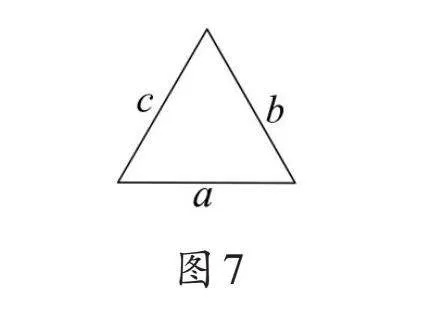
④寫(xiě)出求圖7三角形面積的三種方法。

最后，教師在融合模式指導(dǎo)下同時(shí)改變?nèi)切蔚男螤睢⒌走吪c水平面關(guān)系、作高的頂點(diǎn)，設(shè)計(jì)素材⑤。

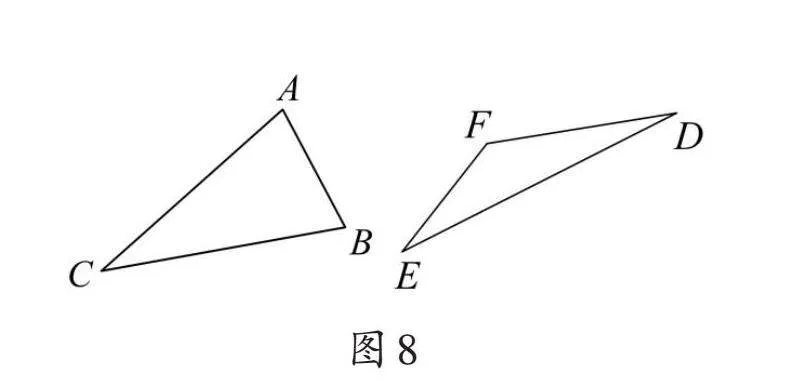
⑤如圖8，請(qǐng)分別以C和D為頂點(diǎn)作高，并通過(guò)測(cè)量高和對(duì)應(yīng)底邊的長(zhǎng)度，分別求出兩個(gè)三角形的面積。

通過(guò)應(yīng)用變異理論，教師滿(mǎn)足學(xué)生不同層次的認(rèn)知需求，促使學(xué)生在面積計(jì)算學(xué)習(xí)中實(shí)現(xiàn)思維進(jìn)階，形成更加牢固的理解，提高遷移與運(yùn)用能力。

四、通過(guò)“一題多變”教學(xué)應(yīng)“萬(wàn)變”

在變異理論指導(dǎo)下，我們引入不同形式和結(jié)構(gòu)的題目，呈現(xiàn)多樣化的問(wèn)題情境，能使學(xué)生在解決問(wèn)題的過(guò)程中經(jīng)歷各種信息的變異，對(duì)概念形成更加深刻、全面的認(rèn)識(shí)，同時(shí)熟悉同一類(lèi)型題目的不同變式。

如，教學(xué)人教版數(shù)學(xué)五年級(jí)下冊(cè)“分?jǐn)?shù)的意義和性質(zhì)”單元時(shí)，我們可以通過(guò)“一題多變”教學(xué)，幫助學(xué)生應(yīng)對(duì)題目的“萬(wàn)變”。在比較分?jǐn)?shù)大小的教學(xué)中，我們可以靈活改變需要比較大小的兩個(gè)分?jǐn)?shù)的形式，例如分別選擇分母相同、分子相同，以及分子、分母都不同的分?jǐn)?shù)進(jìn)行比較；選擇真分?jǐn)?shù)、假分?jǐn)?shù)、帶分?jǐn)?shù)等不同類(lèi)型的分?jǐn)?shù)放在一起比較。通過(guò)體會(huì)題目之間的共性與差異，學(xué)生能夠迅速定位關(guān)鍵信息，辨別題目涉及的核心知識(shí)點(diǎn)，進(jìn)而找到解題的核心要素，即將各種形式的分?jǐn)?shù)化成同分母或同分子的分?jǐn)?shù)后再進(jìn)行比較。這樣教學(xué)有助于學(xué)生形成在不同情境下迅速洞察問(wèn)題的數(shù)學(xué)本質(zhì)的能力，從而準(zhǔn)確地遷移運(yùn)用已有的解決問(wèn)題思路和方法更好地應(yīng)對(duì)各種新情境下的同類(lèi)問(wèn)題。

（楊楠、郭睿系北京師范大學(xué)教育學(xué)部碩士研究生）

責(zé)任編輯 劉佳