中華優秀傳統文化融入高中數學課堂的路徑

隨著全球化的不斷推進和多元文化的交融，中華優秀傳統文化在教育領域中的地位愈發受到重視。高中數學中融入中華優秀傳統文化元素，不僅可以豐富教學內容，還能激發學生對數學文化的興趣，培養學生的民族自豪感和文化認同感。中華優秀傳統文化與高中數學之間并非孤立存在，而是有著千絲萬縷的聯系的，從數學的起源和發展來看，古代中國的數學成就如《九章算術》《周髀算經》等，為世界數學的進步做出了不可磨滅的貢獻。這些寶貴的數學遺產，不僅蘊含著中華民族智慧的結晶，也體現了古人對自然和社會的深刻理解。因此，將中華優秀傳統文化融入高中數學課堂，既是對歷史文化的傳承，也是對數學教育的創新。本文探討如何將中華優秀傳統文化融入高中數學課堂，為培養具有綜合素養的優秀人才貢獻力量。

一、引入歷史背景，揭示三角函數的發展脈絡

在教學“三角函數”這一章節時，直接引入數學公式和定義可能會讓學生感到枯燥和難以理解。為了讓學生更好地吸收這一知識，教師決定以三角函數的歷史背景為引子，帶領學生共同探尋這一古老而重要的數學領域的奧秘。

教師：同學們，你們知道嗎？在大家今天學習的三角函數背后，隱藏著一段古老而精彩的數學史。在古希臘時代，數學家對幾何和代數有著極深的熱愛和追求。他們發現，當我們在一個圓上標記一個角度，并從這個角度的頂點引出兩條射線，這兩條射線與圓的交點之間的距離，與角度的大小之間似乎有著某種神秘的聯系。古希臘數學家經過長期的探索和研究，終于發現這種聯系可以用一組特定的函數來表示，這就是大家今天要學習的三角函數。

有學生迫不及待地問道：那么，三角函數具體是什么呢？

教師：這正是大家要探討的。三角函數描述了角度與邊長之間的定量關系，當大家知道一個角度時，就可以通過三角函數計算出與之相關的邊長；反過來，如果大家知道邊長，也可以利用三角函數計算出對應的角度。

接著，教師繼續講述：當數學的重心從古希臘轉移到阿拉伯時，數學家對三角函數進行了更深入的研究，他們不僅繼承了古希臘的數學知識，還進行了許多創新。例如，他們為三角函數賦予了新的名稱，如正弦、余弦等，這些名稱至今仍在使用。

又有學生好奇地問：老師，這些名稱是怎么來的呢？

教師笑著解釋：這背后有一個有趣的故事，正弦這個名稱來源于阿拉伯語的“jayb”，意為“弓弦”，這是因為正弦函數在幾何上可以理解為單位圓上點的縱坐標，與弓弦的形狀相似。而余弦函數則是正弦函數的補角函數，因此得名。

學生恍然大悟，紛紛點頭表示理解，教師趁機補充道：通過這段歷史，大家可以看到，三角函數并非憑空產生，而是經過幾代數學家的共同努力和探索才逐漸形成和完善起來的。

學生：學習三角函數對我們有什么意義呢？

教師：三角函數不僅在幾何學中有著廣泛的應用，還在物理學、工程學、計算機科學等領域發揮著重要作用。掌握了三角函數，大家就能夠更好地理解和解決這些領域中的實際問題。

通過這段歷史背景的講述，學生不僅對三角函數有了更深入的了解，還激發了對后續學習內容的興趣。學生紛紛表示，要認真學習三角函數，爭取掌握這一重要的數學工具。

二、利用傳統數學典籍，解讀三角函數知識

在上課前，教師向學生展示了《周髀算經》《九章算術》等古代數學典籍的復制品，并講道：同學們，今天大家要一起穿越時空，回到古代的數學世界，從那些古老的數學典籍中解讀三角函數的知識。

學生好奇地圍上來，教師翻開《周髀算經》的一頁，指著上面的文字說：大家看，這里記載了關于勾股定理的詳細闡述。勾股定理，又稱畢達哥拉斯定理，揭示了一個直角三角形三邊之間的關系。但大家知道嗎？這個看似簡單的定理，其實與三角函數有著密不可分的關系。

學生：老師，勾股定理就是a2+b2=c2，但它和三角函數是怎么聯系起來的？

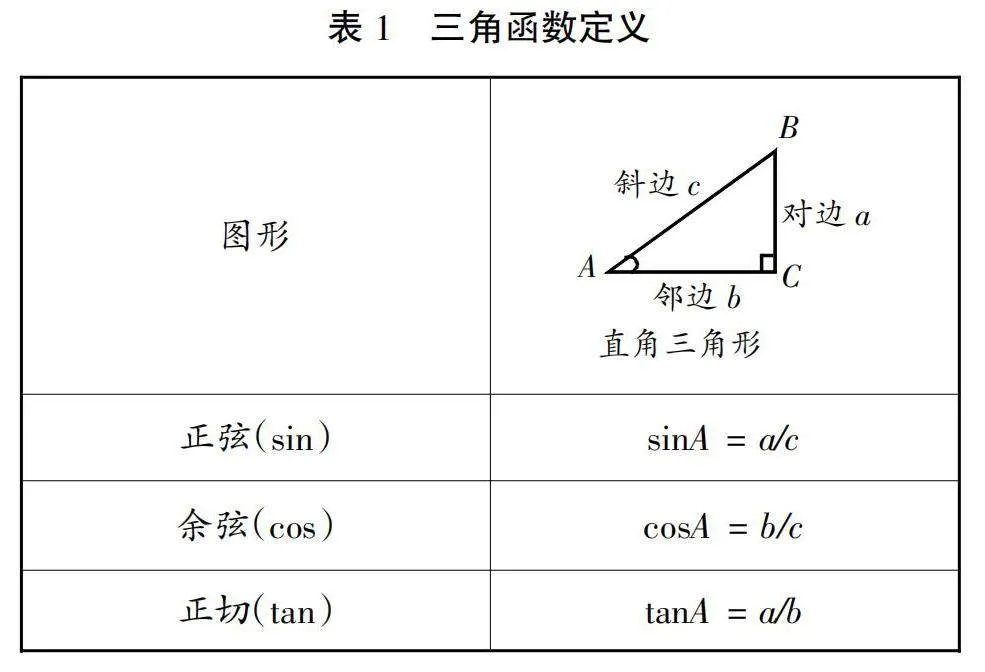
教師：在直角三角形中，如果我們固定一個銳角，比如角A，那么角A的正弦值就是這個角對應邊的長度a與斜邊長度c的比值，即sinA=a/c，這樣，我們就通過勾股定理，將三角函數與直角三角形的邊長關系聯系起來了。

學生紛紛點頭，表示理解。教師繼續講解，并拿起粉筆在黑板上畫了一個直角三角形，標注了各邊的長度，進一步解釋說：比如，有一個直角三角形，直角邊a的長度為3，直角邊b的長度為4，斜邊c的長度為5，那么，角A的正弦值就是3/5。

以此類推，在教師的引導下，學生得出了其他的三角函數定義（如表1）。

學生：老師，那在實際生活中，如何利用三角函數來解決問題呢？

教師：在古代，三角函數被廣泛應用于各個領域。比如，建造房屋時需要確定屋頂的角度，這時就可以利用三角函數來計算；在航海中要確定船只與目的地之間的距離和角度，也需要用到三角函數。它們是連接數學與實際應用的橋梁。

為了讓學生更加直觀地感受三角函數的實用性，教師還準備了一些古代數學家的計算方法和實例，詳細講解了這些方法的原理和應用。學生聽得津津有味，不時發出贊嘆聲。

教師：雖然三角函數是現代數學的一個重要分支，但它的起源和發展都與古代數學密切相關。通過解讀古代數學典籍，我們不僅可以更好地理解三角函數的知識，還能感受到數學的魅力和實用性。希望大家在今后的學習中能夠繼續保持對數學的熱愛和好奇心。

三、融入傳統圖案設計，理解三角函數圖象

三角函數的教學總是帶有一定的抽象性，學生往往難以直觀地理解其圖象的性質。為了打破這一教學困境，教師決定將傳統圖案設計融入課堂，讓學生在欣賞古老文化的同時，深化對數學知識的理解。課堂開始，教師首先展示了太極圖和八卦圖這兩幅在中華優秀傳統文化中具有深厚底蘊的圖案，然后提出問題：同學們，請仔細觀察這兩幅圖，看看你們能否從中發現與三角函數相關的特點。

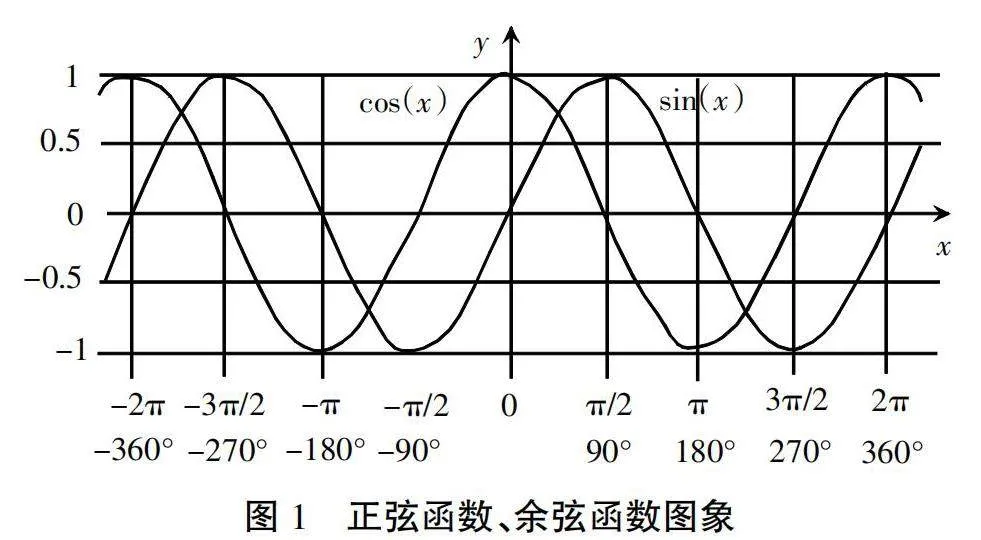
學生紛紛聚精會神地觀察起來。不一會兒，就有學生舉手發言：老師，我覺得太極圖中的陰陽變化與正弦函數的周期性波動非常相似。正弦函數從零開始上升，達到最大值后下降，再回到零。這個過程與太極圖中陰陽的轉換和循環如出一轍。

另一位學生補充道：老師，我發現正弦函數和余弦函數的圖象都是關于y軸對稱的，這與太極圖中兩個相互交錯的魚形圖案的對稱性不謀而合。（如圖1）■

教師：非常好！那大家能否嘗試用三角函數來描述這兩幅圖呢？

學生思考并交流，不一會兒，有學生提出：太極圖中的“S”形分界線，我認為可以看作是正弦函數和余弦函數圖形的結合，當我們把正弦波和余弦波疊加時，就會得到類似于太極圖“S”形的曲線。

教師：你的想法很有創意！確實，三角函數可以描述出太極圖中的“S”形分界線，那么，八卦圖又如何與三角函數建立聯系呢？

在教師的引導下，學生發現八卦中的每一個卦象都可以與特定的角度相對應，例如，乾卦（全陽）對應90度（π/2弧度），坤卦（全陰）對應270度（3π/2弧度），而其他六個卦則分別對應15度（π/12弧度）、45度（π/4弧度）、60度（π/3弧度）、75度（5π/12弧度）、105度（7π/12弧度）和135度（3π/4弧度）等角度。

為了使學生更加深入地理解這種聯系，教師鼓勵學生親自動手繪制這些圖案，并嘗試用三角函數來描述它們。學生在繪制過程中不斷交流、討論，不僅加深了對三角函數圖象的理解，還對傳統圖案設計產生了濃厚的興趣。這堂生動的數學課讓學生感受到數學與文化的交融之美。他們不僅掌握了三角函數圖象的知識，還領略了中華優秀傳統文化的魅力，這種跨學科的教學方式使數學學習變得更加有趣和有意義。

四、通過古詩詞中的描述，感悟三角函數的應用

教師：同學們，你們知道嗎？古詩詞不僅用優美的文字描繪了豐富的情感與意境，還隱藏了許多數學知識，今天，大家就來一起探索古詩詞中的描述，感受三角函數知識的魅力。

教師輕輕點擊多媒體設備，屏幕上緩緩呈現出一幅王羲之的《蘭亭集序》書法作品。教師指向其中一句：“仰觀宇宙之大，俯察品類之盛，所以游目騁懷，足以極視聽之娛，信可樂也。”這句詩描繪了詩人對天地萬物的廣闊感悟。大家有沒有注意到，這里也蘊含著角度的變換呢？

學生：老師，我注意到了。當詩人仰望星空時，他的視線幾乎垂直于地面，這應該是一個接近90度的角，而當他俯視地面時，這是一個接近0度的角。

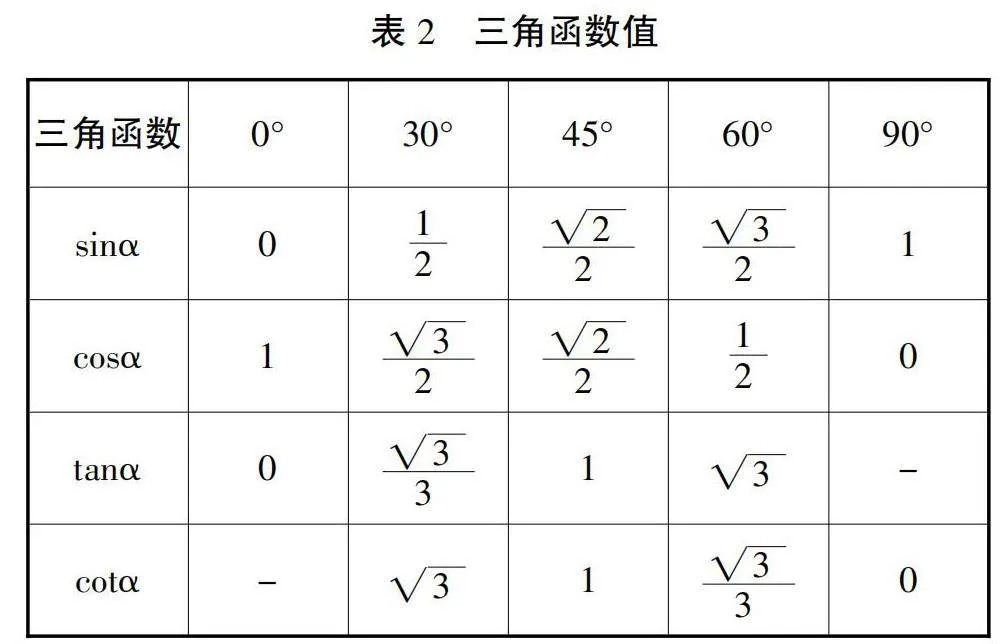
教師：沒錯，這種視角的變化，正是三角函數研究的核心，三角函數是一種研究角度與邊長關系的數學工具。在直角三角形中，當我們知道一個角的大小，就可以通過三角函數求出這個角所對的邊與斜邊的比值，這個比值，就是我們所說的三角函數值，而當我們改變角度時，邊長之間的比值也會發生變化，這就是三角函數的本質。（如表2）

緊接著，教師在黑板上畫了一個直角三角形，并標注了一個30°的銳角，然后提問：假設這個三角形的斜邊長度為2，那么30°角所對的邊長是多少呢？

學生：根據特殊直角三角形的性質，30°角所對的邊長是斜邊長的一半，所以長度是1，那么，sin30°=1/2。

教師：完全正確。接下來，大家再來看一個古詩詞中的例子。李白《黃鶴樓送孟浩然之廣陵》中的名句：“孤帆遠影碧空盡，唯見長江天際流。”這里的“天際”實際上就是一個角度的極限。那么，如果大家知道視線與地平線之間的角度，能否通過三角函數求出視線所能觸及的最遠的距離呢？

學生：我認為可以，如果我們知道視線與地平線之間的角度和觀察點的高度，就可以通過三角函數求出視線所能觸及的最遠距離。

教師：現在，大家來具體計算一下，假設我們站在一座山上，視線與地平線之間的角度為60度，山的高度（h）為100米，那么視線所能觸及的最遠距離（d）是多少呢？

學生拿起筆迅速計算后回答：根據正弦函數的定義，我們有d=h/sin60°，將h=100代入公式，得到d約為115.5米。

教師：通過對古詩詞的研究，大家不僅能夠感受到詩人的情感與意境，還能夠運用數學知識解決實際問題，這就是數學的魅力所在！

五、組織數學文化講座，拓寬三角函數知識視野

為了讓學生更全面地了解三角函數知識及其文化背景，開闊學生的視野，教師決定組織一場數學文化講座。教師特意邀請了一位知名的數學家，希望為學生帶來一場生動且富有啟發的演講。講座開始前，教師向學生介紹：同學們，今天我們有幸邀請到了一位在數學文化領域有著深厚造詣的專家，他將為大家帶來一場關于三角函數的精彩講座。這位專家不僅在數學領域有著卓越的成就，還對三角函數的歷史背景和文化價值有著深入的研究，希望大家能夠珍惜這次機會，認真聆聽。

隨著學生的期待和好奇，專家走上了講臺：同學們，大家好，三角函數的起源可以追溯到古代的天文學和航海學。在古代，天文學家利用三角函數來計算星辰的位置，航海家則依靠它來確定航向，可以說，沒有三角函數，就沒有我們今天的導航系統。而隨著時間的推移，三角函數逐漸發展成為一個獨立的數學分支，并在各個領域得到了廣泛的應用。

專家的話立刻引起了學生的興趣，他們紛紛挺直身體，聚精會神地聽著。為了進一步激發學生的興趣，專家又說道：實際上，三角函數在現代科技中扮演著非常重要的角色，比如，在物理學中，三角函數被用來描述波的傳播和振動；在工程學中，三角函數被用來分析結構的穩定性和強度；在經濟學中，三角函數則被用來研究市場的波動和趨勢。可以說，沒有三角函數，現代科技就無法取得如此輝煌的成就。

一位學生聽后感嘆道：原來三角函數這么有用啊！我以前一直覺得數學只是一堆枯燥無味的公式和定理，現在看來，數學其實是一門非常有趣和實用的學科。

專家微笑著點頭，繼續深入講解：除了實用性之外，三角函數還有著非常重要的文化價值。在古代藝術中，三角函數被用來設計圖案和構圖；在音樂中，三角函數被用來解釋聲音的振動和共鳴現象；在哲學中，三角函數則被用來闡述宇宙的和諧與秩序。

聽到這里，學生紛紛表示受益匪淺，他們不僅了解到三角函數的發展歷程和應用領域，還感受到數學學科的魅力和價值。一位學生感慨地說：通過這次講座，我深刻體會到“數學無處不在”的道理，原來數學并不是一門孤立的學科，而是與我們的生活息息相關的。我要重新審視數學學科，努力學習，掌握它的精髓。

教師看到學生如此投入和興奮，心中感到無比欣慰。他知道這次數學文化講座不僅成功開闊了學生的三角函數知識視野，還激發了學生對數學學科的興趣和熱愛，這將成為學生學習道路上寶貴的財富，引領學生不斷探索數學的奧秘。

六、教學反思

在嘗試將中華優秀傳統文化融入高中數學“三角函數”教學的過程中，通過引入三角函數的歷史背景、解讀傳統數學典籍、利用傳統圖案設計、結合古詩詞描述以及組織數學文化講座，學生不僅掌握了三角函數的基礎知識，還從中體會到數學與文化的緊密聯系。然而，在教學過程中，我們也發現了一些挑戰，例如，如何平衡中華優秀傳統文化的深度與廣度、如何確保數學教學與中華優秀傳統文化融合的自然與流暢等。在今后的教學中，教師仍然需要繼續探索更加有效的融合策略，以更好地培養學生的數學素養和文化自信，同時希望更多的教師能夠關注并嘗試這種融合的教學方式，共同推動數學教學的創新發展。

（作者單位：甘肅省靖遠縣第二中學）

編輯：溫雪蓮