借助圖表解決分段計費問題

《分段計費》是人教版數學五年級上冊的教學內容，學生探究該類問題能夠鞏固小數乘法的知識，積累解決問題的經驗，為后續學習函數做鋪墊。分段計費廣泛應用于生活，如出租車費、水費、手機通話費等，教學中，教師不僅要引導學生掌握解決問題的方法和技能，建構數學模型，還要引導學生感悟其中的數學思想方法，并遷移運用所學知識解決生活中的實際問題。本期，我們精選四篇文章，分別從借助圖表、多元表征、問題驅動等教學策略和作業設計的視角做具體闡述。

學生學習分段計費問題的難點，一是不能正確理解題意，把握其中蘊含的數量關系；二是缺少解決相關問題的生活經驗，認識不到它的社會意義和價值。為幫助學生更加直觀地理解分段計費問題，筆者借助圖表引導學生明確分段計費的收費標準，探究其中的數量關系，構建分段計費模型并正確解答問題，以增強學生解決問題的能力和節約、環保意識。

一、借助發票圖片，初步感知分段計費標準

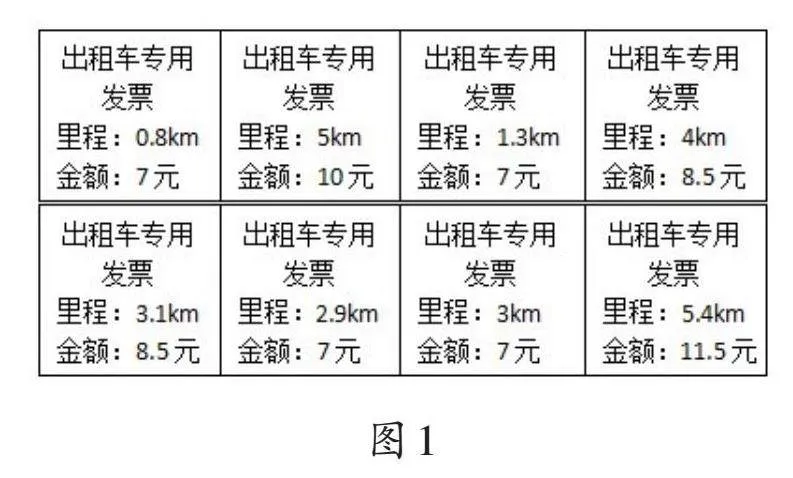
分段計費是典型的問題解決內容。為激發學生探究的欲望，幫助學生初步感知分段計費的標準，筆者出示如圖1所示的8張出租車發票圖，引導學生有序整理圖片，說一說有什么發現。

學生按照里程數從小到大的順序排列發票，發現出租車的收費金額和里程數有關系。一名學生說：里程數為0.8千米、1.3千米、2.9千米和3千米時，收費都是7元。另一名學生質疑：“5千米比4千米多1千米，多收1.5元，而3.1千米比3千米只多0.1千米，也要多收1.5元。這是為什么呢？”筆者引導：“猜一猜，出租車是怎樣收費的？”有的學生猜測：“里程數在3千米及以內的都是收費7元。”有的學生補充：“這說明出租車的起步價是7元。”有的學生推測：“里程數超過3千米時，每多1千米，就多收1.5元。”又有學生補充：“我猜測最后一段不足1千米的部分按1千米計算。”筆者肯定了學生的想法，并梳理出如下出租車收費標準：3千米及以內7元；超過3千米的部分，每千米1.5元（不足1千米按1千米計算）。隨后，筆者出示教材例9：“右面是某地出租車的計價標準。李叔叔乘坐出租車行駛了6.3千米，他應付出租車費多少錢？”學生看到例9中給出的出租車收費標準與他們猜測的一致，興奮不已，躍躍欲試。

以上教學，筆者從乘坐出租車的生活情境入手，引導學生觀察、整理出租車發票圖片，提出疑問，猜測出租車的收費標準，激發了學生的探究興趣。同時，出租車發票為學生感知出租車的收費方式提供了素材，有助于學生發現出租車分段計費的特點。

二、借助畫圖理解題意，探索分段計費問題解法

畫圖等直觀方法能幫助學生理清問題中的數量關系，探索解決問題的思路并預測結果。因此，教師可引導學生利用數形結合思想，通過畫圖理解題意，把握數量關系，學會解決分段計費問題。

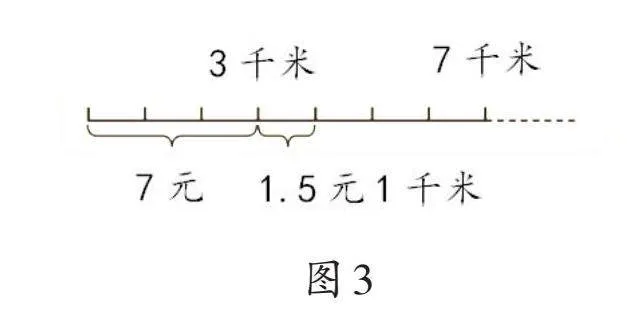
課堂上，筆者出示例9后提出學習任務：“認真閱讀題目，說一說你從中得到了哪些信息。寫一寫或畫一畫，用你喜歡的方式表示這些信息。”學生借助已有經驗想出了不同的方法：有的學生畫簡易關系圖整理關鍵信息（如圖2），有的學生畫線段圖整理關鍵信息（如圖3）。

筆者追問：“你是怎樣畫線段圖的？”學生說：“用線段將路程分為兩段。第一段表示小于等于3千米的路程，第二段表示超過3千米的路程。因為‘不足1千米按1千米計算’，所以我把6.3千米看成7千米，即線段終點表示7千米。”在此基礎上，筆者引導學生對比觀察圖2、圖3的表示方法，學生發現用線段圖表示更形象、直觀。筆者繼續追問：“這兩段分別怎樣計算費用？”學生根據線段圖回答：“第一段只付7元，第二段每多1千米加1.5元。”

筆者提出新任務：“觀察整理的信息，思考有哪些解答方法，并用你喜歡的方法解答。”學生獨立作答后交流匯報。一名學生說：“6.3千米要按7千米計算，所以第二段超出的部分用‘7-3’計算，得出4千米，再用‘4×1.5’計算出收費6元，最后用6元加上第一段的收費7元，得出要付13元。”筆者引導：“你能給這種方法取個名字嗎？說一說理由。”學生稍加思考后說：“分段計算法。這個名字提醒我們要根據不同標準分段計算費用。”另一名學生匯報：“把6.3千米看成7千米，假設7千米都按照每千米1.5元計算，則用“1.5×7”計算出共需支付10.5元。由于前面的3千米也按照每千米1.5元計算，只收了4.5元（1.5×3=4.5），所以應補收2.5元（7-4.5=2.5）。最后用‘10.5+2.5’計算出共付13元。”筆者適時點撥：“我們把這種方法叫做假設法。運用假設法解決問題要注意什么？”學生回答：“要注意補上少算的部分。”筆者小結：“一段里程分成兩段收費，這樣的計費方式在數學上叫做分段計費。”

這樣教學，學生將題目的文字表征轉化為圖示表征，準確把握了“超過”“不足”等關鍵詞，比較直觀地找到了分段的節點，理清了出租車分段計費的原理，最終通過計算解決了問題。

三、表格與圖象相結合，構建分段計費模型

分段計費問題實際上是分段函數的體現，教師要借助分段函數圖象有效地滲透函數思想，使學生發現分段計費問題中的變與不變，更好地理解與構建分段計費模型。

在回顧與反思環節，筆者引導學生自主完成下面的出租車價格表，建立解決這類問題的一般方法。

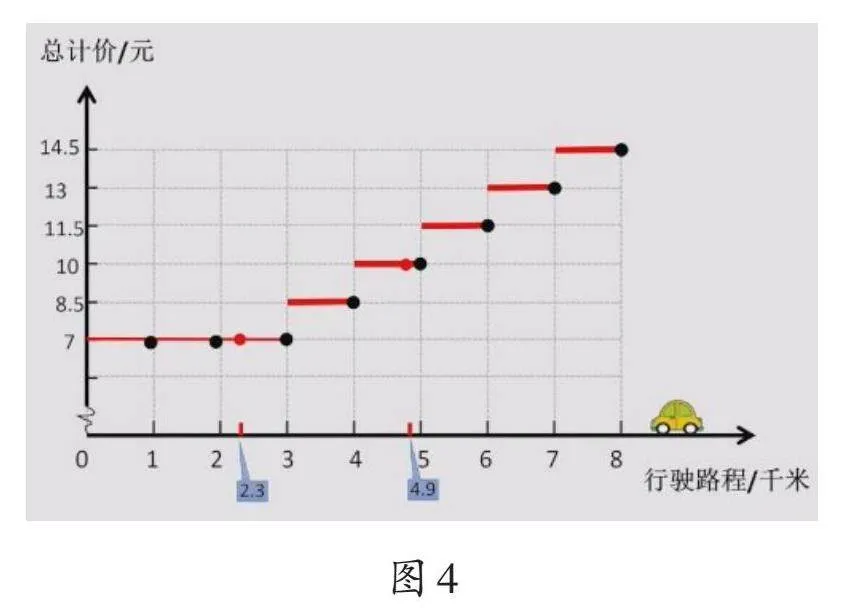
學生根據前面得到的結果填寫出租車價格表后，筆者用動畫呈現出租車行駛里程和相應車費的變化情況，最終呈現出圖4即分段函數圖象。

筆者引導：“圖4中橫著的線叫橫軸，表示行駛里程，豎著的線叫縱軸，表示價格。觀察圖象，你有什么想法？”學生觀察后交流：“長一些的紅線表示3千米及以內的部分，短一些的紅線表示超出的部分。”筆者指著橫軸上的2.3追問：“走這么遠的路程，車費是多少呢？”學生看圖答道：“7元。”筆者再問：“3千米及以內7元是什么意思？”學生回答：“只要車子啟動，不超過3千米就付7元。”筆者指著橫軸上的4.9繼續問：“看短一些的紅線，走這么遠的路程，車費是多少呢？”學生看圖答道：“4.9千米可按5千米計算，5千米比3千米多2千米，要增加2個1.5元，即增加3元，之后用“7+3”計算出應付10元。”筆者引導：“從圖象上看，哪一段每千米價格更高？”學生很快發現第一段每千米價格更高。筆者小結：“分段計費的每一段就像一個階梯，所以又稱為‘階梯收費’。”

這樣教學滲透了函數思想，幫助學生更好地理解與建構了分段計費模型。

（作者單位：老河口市實驗小學）