數(shù)學文化視角下的高中數(shù)學閱讀材料之使用

［摘 要］ 相對于抽象的數(shù)學知識，數(shù)學教材中的閱讀材料更具趣味性. 實踐證明，借助數(shù)學閱讀材料滲透數(shù)學文化具有重要的教學價值，值得每一個教師去研究與思考. 文章以“橢圓的定義”教學為例，以閱讀材料“刁尼秀斯之耳”為主線，從“呈現(xiàn)閱讀材料，引出橢圓”“逐步探索問題，挖掘性質(zhì)”“實踐操作探索，深入理解”“抽象概括總結(jié)，構建概念”四方面展開分析，并有針對性地談一些思考與感悟.

［關鍵詞］ 數(shù)學文化；閱讀材料；橢圓

數(shù)學文化涵蓋數(shù)學思想的演變、方法的應用、觀點的提出，以及數(shù)學史、數(shù)學家、數(shù)學教育、數(shù)學美等人文元素. 《普通高中數(shù)學課程標準（2017年版2020年修訂）》強調(diào)教師在教學中應有意識地結(jié)合教學內(nèi)容的特點滲透數(shù)學文化，讓學生了解數(shù)學在科技與社會發(fā)展中的推動作用，認識數(shù)學的科學價值、應用價值、文化價值和審美價值，從真正意義上提升學生的應用意識、人文精神與科學素養(yǎng).

高中數(shù)學教材中的數(shù)學文化有顯性融入與隱性融入兩種方法，知識本身所攜帶的數(shù)學文化為隱性融入，而以閱讀材料呈現(xiàn)的數(shù)學文化則為顯性融入. 學生通過對學科知識背景的了解，可不斷開闊視野，挖掘潛能. 為此，本文結(jié)合“橢圓的定義”教學具體談一談如何應用顯性閱讀材料，滲透數(shù)學文化，發(fā)展學生的數(shù)學學科核心素養(yǎng).

教學過程

1. 呈現(xiàn)閱讀材料，引出橢圓

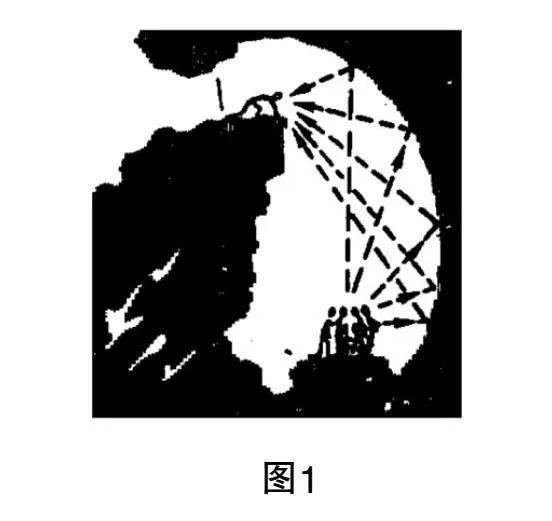
閱讀材料 如圖1所示，此為西西里島的巖洞內(nèi)所關押的犯人與看守者，犯人因無法承受長期孤獨的生活計劃越獄. 每次越獄之前，犯人都會做一套詳細的越獄方案，但每次都以失敗告終，這就導致他們互相猜忌、懷疑，認為犯人中有告密者. 然而，不論怎么排查，都沒有發(fā)現(xiàn)誰是告密者. 一個犯人偶然發(fā)現(xiàn)巖洞的形狀為橢圓形，不論犯人在巖洞內(nèi)多么小聲地交談，聲音都能經(jīng)過巖洞壁反射到洞口被看守者聽到，所以看守者對犯人的一舉一動都了如指掌. 自此，該巖洞被稱為“刁尼秀斯之耳”.

師：這是一個神奇的故事，看守者為何能聽見犯人談話內(nèi)容呢？

生1：犯人發(fā)出的聲音，經(jīng)過巖洞壁的反射，最終匯聚到洞口，被看守者聽到.

師：巖洞壁的曲線形狀是什么呢？

生2：如圖2所示，這是一個橢圓形.

師：這是結(jié)合閱讀材料所獲得的形狀，既然大家都覺得是橢圓形，那么該怎樣完整地形容橢圓呢？說一說它的形成原理.

設計意圖 閱讀材料的展示，一方面刺激學生的感官系統(tǒng)，引發(fā)學生對本節(jié)課的興趣；另一方面，讓學生初步認識該現(xiàn)象形成的原理，為抽象橢圓模型奠定基礎. 根據(jù)學生已有的認知經(jīng)驗構建問題，可有效啟發(fā)學生思維，引導學生明確探索方向.

2. 逐步探索問題，挖掘性質(zhì)

問題1 橢圓的形成因素有哪些？哪些因素決定橢圓的形成？

結(jié)合閱讀材料內(nèi)容，學生稍作思索就發(fā)現(xiàn)看守者與犯人所處的地理位置決定了橢圓形成的要點. 若將巖洞的軸截面理解為一個橢圓，則看守者與犯人所處的位置可理解為橢圓內(nèi)兩個恒定不變的點，聲音傳播可想象為從其中一點發(fā)出的射線撞擊橢圓壁后反射經(jīng)過另一點（如圖3所示）.

問題2 如圖4所示，如果F，F(xiàn)為橢圓內(nèi)的兩個定點，而點P在橢圓上，那么

PF，

PF，

F

F存在怎樣的數(shù)量關系？

生3：連接FP，F(xiàn)P，F(xiàn)F，形成△FFP，則

F

F-

FP<

FP或

F

F+

FP>

FP.

師：不錯，除此之外，三者還有沒有其他數(shù)量關系？

生4：

FP+

FP>

F

F或

FP-

FP<

F

F.

問題3 通過以上探索，可以確定

FP+

FP為固定值嗎？

如圖5所示，借助幾何畫板進行演示，發(fā)現(xiàn)雖然

FP與

FP的值可以自由變化，但是它們的和卻不會因為點P位置的變化而變化，由此明確當F，F(xiàn)為定點時，

FP+

FP的值為固定值.

問題4 橢圓上的任意點與定點F，F(xiàn)之間的距離之和有什么特點？

依然應用幾何畫板進行演示驗證，引導學生自主發(fā)現(xiàn)橢圓上的任意點與定點F，F(xiàn)之間的距離之和恒為常數(shù)2a，且2a>2c（2c為兩定點F，F(xiàn)之間的距離），橢圓的幾何特征浮出水面.

設計意圖 結(jié)合閱讀材料，學生很快就自主發(fā)現(xiàn)并提出橢圓上的點所滿足的數(shù)量關系. 而且，靈活、恰當?shù)貞脦缀萎嫲迥艽偈箤W生在強烈的認知沖突中發(fā)現(xiàn)變化中的不變——P是橢圓上的任意一點，

FP+

FP為定值. 將橢圓的幾何特征挖掘出來，再次有效推動學生數(shù)學學科核心素養(yǎng)的提升.

3. 操作實踐探索，深入理解

師：我們運用幾何畫板探究并驗證了橢圓所具備的幾何性質(zhì)，除此之外，大家還能想到其他驗證方法嗎？

活動要求：如圖6所示，已知F（圓內(nèi)非F的一點）是圓F內(nèi)的一定點，A是位于圓周上的任意點，怎樣借助對折紙片的方法找出線段AF的垂直平分線？

生5：如圖7所示，對折紙片使點A與點F重合，折痕就是線段AF的垂直平分線.

師：很好！如圖8所示，在圓上多處取點A，并不斷重復這個折疊過程，會有什么新的收獲？

生6：通過不斷折疊，發(fā)現(xiàn)無數(shù)條折痕最終圍成了一個橢圓.

師：折痕與橢圓之間有一個怎樣的位置關系？

生7：兩者相切.

師：有什么辦法證明？

生8：先要明確點P是否位于橢圓上. 如圖9所示，若2a為圓的半徑，直線l為折痕所在的直線，AF，AF與直線l分別相交于點P，C. 因為直線l為AF的垂直平分線，所以AC=CF，∠ACP=∠FCP，為直角. 由此不難獲得△CPA≌△CPF，所以PA=

PF. 所以

PF+

PF=

FP+AP=

AF=2a，也就是點P位于橢圓上.

師：根據(jù)以上探索可知，點P不僅位于橢圓上，還是橢圓與直線l的交點，那么，它是橢圓與直線l的切點嗎？

生9：從相交與相切的角度來看，若直線l與橢圓相交，則存在兩個交點，而相切只有一個交點. 若點P是橢圓與直線l的唯一交點，則點P就是切點.

師：有沒有什么辦法可以證明？

生10：如圖10所示，在△ANF中，

FN+AN>

FA. 根據(jù)等量替換法可知

FN+

FN=

FN+AN>

AF=2a.據(jù)此能確定點N并不在橢圓上，也就是說直線l上只有一個點P處于橢圓上，所以點P是橢圓與直線l的切點.

設計意圖 實踐操作不僅能提升學生的探究能力，還能優(yōu)化學生的思維，幫助學生建構良好的認知結(jié)構，使學生從真正意義上領悟折痕與橢圓之間的位置關系.

4. 抽象概括總結(jié)，建構概念

問題5 怎樣結(jié)合橢圓的幾何特征總結(jié)橢圓的概念？怎樣根據(jù)橢圓的概念畫橢圓？

設計意圖 從橢圓的概念出發(fā)，引導學生自主總結(jié)與提煉，不僅能進一步優(yōu)化學生數(shù)學思維，促使學生應用數(shù)形結(jié)合思想體會橢圓概念的本質(zhì)，確定作圖的具體方法，還能讓學生基于多元表征，深化對數(shù)學本質(zhì)的理解，建構完整的認知體系，為應用與創(chuàng)新奠定基礎. 同時令深度學習真實發(fā)生，促進學生數(shù)學直觀想象與邏輯推理素養(yǎng)的發(fā)展.

教學案例分析

本節(jié)課，以閱讀材料為起點引入教學主題，并圍繞閱讀材料提出探究問題，引導學生從折紙活動與幾何畫板的演示中發(fā)展自主探究能力，培育數(shù)學抽象和直觀想象素養(yǎng)，同時滲透數(shù)學文化. 從數(shù)學角度分析折痕與橢圓的位置關系，進一步激活學生的思維，促使學生自主總結(jié)橢圓的概念，幫助學生提煉數(shù)形結(jié)合思想.

在訪談中發(fā)現(xiàn)，學生很喜歡此類探究課，因為閱讀材料讓課堂變得更加豐富，這是將生活與數(shù)學聯(lián)系起來的教學方式. 學生還提出，許多著名建筑均融入了數(shù)學知識，彰顯生活與數(shù)學的緊密聯(lián)系. 數(shù)學是現(xiàn)實社會的抽象表達，通過符號運算、形式推理和模型建構，揭示事物的本質(zhì)、關系和規(guī)律. 這是一節(jié)成功的課堂，學生從中不僅感知到閱讀材料的重要性，還體驗到信息技術的介入使得數(shù)學知識更加直觀易理解.

關于閱讀材料的幾點思考與感悟

1. 用于課后閱讀

教材上的閱讀材料與數(shù)學文化有較大關系，很多內(nèi)容都是知識的形成歷程，這些閱讀材料是對教材正文的補充與拓展. 教師結(jié)合學情與教情利用好閱讀材料，采取恰當?shù)慕虒W策略幫助學生更好地理解與掌握所學知識. 若閱讀材料涉及數(shù)學史、小故事或數(shù)學家，教師可鼓勵學生課后自主閱讀，感受數(shù)學知識的形成與發(fā)展，并撰寫心得進行交流.

2. 用于課堂參考

教材上的閱讀材料往往蘊含豐富的數(shù)學思想方法. 數(shù)學思想方法的形成對學生可持續(xù)發(fā)展至關重要. 課堂上，教師可帶領學生一起解讀閱讀材料，讓學生從中體會知識的來龍去脈，為完善認知結(jié)構奠定基礎.

3. 用于引領閱讀

若課堂時間充裕，教師可根據(jù)實際情況為學生列出學習提綱，鼓勵學生帶問題閱讀材料. 這種任務明確的閱讀方法能為學生指明思考方向，讓學生在交流與總結(jié)中碰撞出智慧的火花. 因此，結(jié)合閱讀材料設計問題，引領學生閱讀，可激活學生的思維，激發(fā)課堂的智慧與活力.

總之，數(shù)學閱讀材料不可或缺，具有獨特價值. 作為教師，應關注閱讀材料在滲透數(shù)學文化方面的重要性，有效利用閱讀材料，促進學生成長.