聚焦數據意識 凸顯平均數統計意義

摘要：數據意識是指對數據的意義和隨機性的感悟。平均數的教學是培養數據意識的重要內容。特級教師徐斌執教“平均數”，圍繞一場比賽中產生的各種數據進行討論，一步步引出平均數意義。課堂上聚焦數據，引導學生在熟悉的情境中理解平均數的代表性、區間性、虛擬性和敏感性。

關鍵詞：數據意識；平均數；移多補少；統計意義

中圖分類號：G623.56 文獻標識碼：B 文章編號：1673-4289（2024）06-0039-05

數據意識是指對數據的意義和隨機性的感悟，平均數的教學離不開數據。如何讓學生對數據感興趣？如何讓學生直觀感悟平均數的統計意義？游戲是一個好的載體。全國知名特級教師徐斌執教四年級“平均數”，課堂上徐老師邀請孩子們擔當套圈游戲裁判，在徐老師激情推動下，孩子們不知不覺“入彀”，在討論交流中聚焦數據意識，在思考辨析中感悟平均數統計意義。

[課堂片段]

師：這節課，我們從套圈游戲開始，徐老師想邀請在座的各位當套圈比賽的裁判，你愿意嗎？請看，是哪些人在進行比賽呢？

生：是四年級第一小組的男生和女生。

師：男生隊出場了！派出了幾個人？為了公平公正，女生隊呢？男生隊先套，每人發15個圈，這4個人套中的一樣多嗎？

生：不一定。

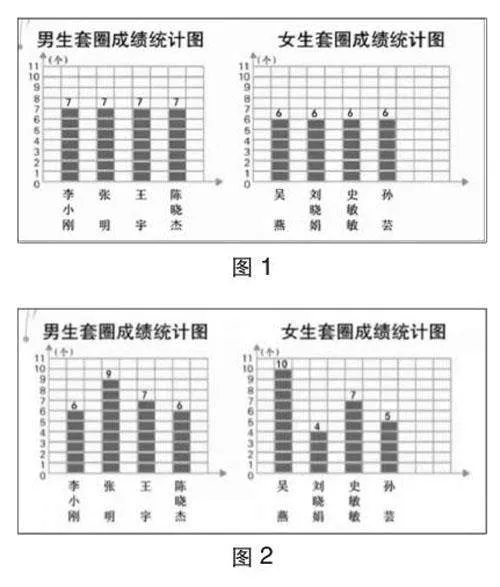
師：不過這次真巧，男生隊每人都套中7個，可以用幾表示男生隊的整體水平？再看女生，整體水平用幾表示？（圖1）哪個隊贏了？

（開展第二輪比賽）

師：輪到女生隊了。哎！有套得多的，也有套得少的。（圖2）第二場比賽哪個隊贏了呢？你們是怎么想的？

生：求平均。

師：求平均？需要那么麻煩嗎？

生：可以把他們一共套中的加起來，然后再比大小。

師：可不可以？大家一起算一算。

生1：男生隊是28個。

師：你是怎么算的？

生1：6+9+7+6等于28個。

生2：女生套中10+4+7+5=26。

師：男生一共套中28個，女生一共套中26個。第二場比賽哪個隊贏了？

[賞析]游戲是迷人的，但比游戲更迷人的是數學思考。徐老師邀請孩子們當套圈游戲的裁判，十分自然地把孩子的注意力由好玩引向對“套中個數”的關注。圖1以條形統計圖為載體，直觀呈現圖形與數據，初步感知平均數特征。第二場比賽各隊還“平均”嗎？作為裁判你是怎么想的？用真實的問題倒逼學生思考，在問題驅動下，孩子們踴躍發言，且能嘗試著用數據說話。

[課堂片段]

師：這時女生隊又提了個要求、說我們再比一場吧！還是男生隊先套，哎！真巧，好像和第一次一樣。

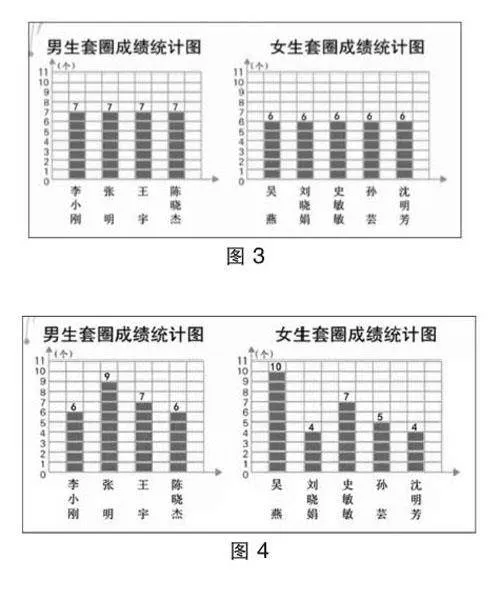
師：輪到女生套了，這時女生弱弱地提了個要求，說我們再派個人吧，男生竟然答應了。于是女生又派了一個人，她也套中了6個（圖3）。

師：第三場比賽結束了，請同桌的兩個裁判，交換一下你們的判斷。認為女生贏的舉手！舉手多就一定對嗎？能不能派個代表說一下你為什么認為女生贏了？

生：因為我們看到，女生的統計圖有5個6，5×6=30，男生是4個7，4×7=28，30比28大。

師：一般人都是這么想的吧。但是我發現你一直沒有舉手，我想請你表達一下，你認為哪個隊贏了？

生：男生。

師：為什么？

生：因為男生的“直條”要高一些。

師：有道理！我們剛才說是男生隊贏還是女生隊贏要比什么？

生：平均每個人的。

師：那叫什么水平？

生：整體水平。

師：大家把手伸出來比畫一下，男生隊的整體水平是幾？女生我也不看你人數，只看整體水平，是幾？

師：同學們眼睛睜大一點，哪個隊整體水平高？

生：男生。

師：對呀，因此第三場比賽其實是哪個隊贏了？

[賞析]當人數不等時比總數還公平嗎？作為裁判你覺得“怎么比”才公平？兒童是天生的學習者，兒童的“直覺”是敏感而細膩的，通過看圖，有孩子發現，男生是“平均”的，女生也是“平均”的，但男生的“直條”要高一些，這是孩子們對“平均”的一種原始的、樸實的、直觀的感覺。當人數變化時，作為裁判的我們不能只盯著總數，而要看他們的整體水平。

[課堂片段]

師：這時女生隊又提了個要求，說我們再來一場決賽吧！好，男生先套，真巧，好像和第二次一樣（圖4）。輪到女生了，已經有5個女生在臺上啦，像這樣只比總和公平嗎？

生：不公平。

師：再看男生套中的有多有少，女生套中的也是有多有少，能像前面那樣一眼看出整體水平嗎？這時候就需要一個新的統計量來幫忙，就是我們今天要學習的，叫做什么呢？

生：平均分。

師：二年級學什么運算的時候學過平均分？

生：除法。

師：不過我們今天不學平均分，今天學習的叫平均數。平均數也有“平均”兩個字，那跟我們已學過的平均分會不會有聯系呢？

生：沒有。

師：不要輕易下結論喲，接下來我們來找平均數。我一看這個9挺可愛的，我想用9代表男生隊的整體水平，你覺得能代表嗎？那我換一個，我換最小的6，6能代表嗎？那你們說，這個代表整體水平的平均數，應該比9要怎么樣？

生：小。

師：比6要怎么樣？

生：大。

師：你們是說平均數是有范圍的。它在最大和最小之間。眼力好的人估計已經找到了，誰找到了？

生：是7。

師：你是怎么找到的？

生：因為7比9要小，7又比6要大。

師：那為什么不找8呢？

生：沒有8。

師：哈哈真可愛，請坐，有沒有哪個說得更清楚一點？

[賞析]游戲是把“學”更好地寓于“玩”中，通過“玩”實現更好地“學”。第四場比賽，人數不同，每個人套中的個數電不同，這時如何比輸贏？在看似“山窮水盡”時引入一個新的統計量“平均數”讓課堂再次“柳暗花明”。誰能代表這個平均數呢？在詼諧幽默的對話中，孩子們不僅知道平均數可以用來代表小組的整體水平，而且知曉平均數是有“區間”范圍的。

[課堂片段]

師：如果9上面這兩個方格能夠移動的話會怎么樣？誰來說說？這位女生，對！就是你。

生：就是把9上面兩個格子一個放到前面6的上面，另一個放到后面6的上面。

師：大家看，9拿一個格給前面的6，再拿一個格給后面的6，現在所有人看上去都是幾了（圖5）？

生：7。

師：對，7就是什么數？

生：平均數。

師：這種方法挺好的，把多的移過來補給少的，可以叫什么？

生：移多補少。

師：這是眼力好的人能看出來的。誰能根據剛才第一步算的結果，再進一步算出平均數？

師：這位同學算出來的平均數是幾啊？

生：7。

師：我有問題，這28和4是哪里來的？

生：28是6+9+7+6加出來的，這個4就是那4個男生。

師：為什么要用除法？

生：因為它是求平均數。

師：我還不明白為什么要除以47誰能說得更清楚些？

生：因為28是加起來的總個數，他們有4個人，所以要把它平均分成4份。

師：掌聲送給這位同學！請坐！大家有沒有注意他剛才用了一個詞啊？對，就是把28平均分給4個人，這樣得到了平均數7。

師：平均數跟以前學過的平均分有沒有聯系啊？是有聯系的，先求出它們的和，簡稱“求和”，然后再除，這種方法連起來就叫“求和平分”。

[賞析]將條形統計圖置于方格圖中，直觀的視覺沖擊讓學生有一種通過移多補少“勻一勻”的沖動。將所有的個數“勻一勻”，勻成一樣多后再進行比較，這個“一樣多”的數叫平均數，最能代表男、女生的整體水平，用其進行比較更合理。“為什么要除以4”不僅回應了“平均數”與“平均”的聯系，而且揭示了求平均數的算術方法。

[課堂片段]

師：男生隊算出來了，該算哪個隊了？用什么方法呢？

生：移多補少。

師：大家說平均數是幾？哪個同學愿意介紹一下你是怎么想的？

生：從10里拿出4個，分兩個給4，再分兩個給另外一個4，這樣兩個4都變成了6。

師：而5和7還不是一樣大呀。

生：我再把7分一個給5，這樣所有的數就都是6了（圖6）。

師：同意吧？這種方法叫什么？

生：移多補少法。

師：是不是有點復雜呀？有些同學是用“求和平分”算出來的。誰來說說看？

生：先用10+4+7+5+4算出30，30除以5，算出6。

師：課上到現在，咱們簡要回顧一下，今天我們認識了一個新的統計量，叫做什么？

生：平均數。

師：哪個同學說說看，你覺得平均數是個什么樣的數？

生：每隊的平均量。

師：平均量。原來不一定平均，最后平均了。說得不錯！還有誰要補充？

生：一組數的平均值。

師：嗯，平均值，有道理。有女生套中6個嗎？

生：沒有。

師：那為什么女生套中個數的平均數可以用6表示？大家可以討論討論。

生1：平均數表示的是這一組數據的集中趨勢，它更接近于一個中間的數。

生2：平均數有可能是一個“虛數”，小組中既可能有這樣“數”，也可能沒有這樣的“數”。

生3：平均數是一個平均值，猶如我們班級的平均成績可能帶小數，而實際上我們每個人的成績都是整數。

[賞析]數學不僅是運算和推理的工具，還是表達和交流的語言。“平均數是個什么樣的數？”孩子們用自己的語言表征對平均數的理解，平均量、平均值、集中趨勢、接近于一個中間的數、“虛數”等，這些“原生態”的描述說明孩子們對平均數的理解既感性又理性，既直觀又深刻。“6能作為女生套中個數的平均數嗎？”問題引導學生討論平均數的實際意義，進一步理解平均數的“代表性、虛擬性”，明確它可能“在”也可能“不在”這一組數據中。

[課堂片段]

師：剛才大家在求平均數的時候想出了兩種方法，一種方法叫什么？另一種方法叫什么？

生：移多補少，求和平分。

師：徐老師就在想啊，以后讓我求平均數，什么時候用移多補少法，什么時候用求和平分法呢？我們來看一個實際問題。這里有三個筆筒，鉛筆分別是幾支？（圖6）

生：6支、7支、5支。

師：這三個數的平均數你能很快得到嗎？用什么方法特別快？

生：移多補少。

師：“變、變、變”，我把條形圖變成3條絲帶，大家看看哪一條最長？

生：藍色。

師：哪一條最短？

生：粉紅色。

師：我現在用剪刀把它剪下來，移多補少，使他們最后變成一樣長，哪位同學愿意來指揮徐老師？

（請了好多學生，又是說，又是比畫，但誰也說不清楚，誰也說服不了誰。漸漸地問題變得聚焦，這個剪去或添上“一點點”，“一點點”是多少啊？）

師：誰有辦法？

生：可以把它們畫成一些格子，這樣就知道他們有多少個格子。

師：不錯，這個辦法已經比剛才先進一點了，有沒有更先進一點的想法？

生：先算出粉色加藍色加黃色的總長，再除以3。

師：要總長，你得有什么呀？

生：數據。

師：對，沒有數據是不行的。

師：掌聲先送給這位同學。他覺得剛才為什么不清楚，得有什么呀？

生：數據。

師：為什么一開始怎么都說不清楚？現在我們能說清楚，誰幫了我們的忙？

師：對，數據。數據是有力量的。

[賞析]在大數據時代，用數據來分析和解決現實問題應成為一種習慣、一種觀念、一種素養，這是學生終身學習和可持續發展的基本途徑，是培養創新意識和實踐能力的基礎載體。“分彩帶”是徐老師的一個創舉。無論孩子們怎么想、怎么比畫，反正就是無法平均分，其實這不是學生的原因，而是題目本身沒有數據支撐，進而讓我們理解了“數據”在統計中的價值。

[課堂片段]

師：同學們用過數據嗎？用數據算過平均數嗎？在生活當中你經常用平均數嗎？接下來我請所有同學都來用一次，徐老師想邀請在座的所有同學當一回隊長。什么隊呢？

師：請看，籃球隊一共有隊員幾人？

生：5個。

師：隊長有時候會優先獲得數據，如果說我們籃球隊5個人的平均身高是160厘米，徐老師看了看說，怎么有一個人的身高只有150多厘米啊？哪個隊長能解釋一下，有可能嗎？

生：有可能。因為每個人的身高都是不一樣的，況且上面還說的是平均。

師：你們覺得解釋得有沒有道理？

生：有道理。平均數是在最高身高和最小身高之間。

師：是的。現在籃球隊又來了1人，這個人加入后現在變成了幾個人？（圖7）

生：6個人。

師：我把6個人身高的總和除以6，得到一個新的平均數，得出后我嚇了一跳，因為得到的這個新的平均身高比較大。你們估計誰來了？

生：姚明。

師：姚明有多高啊？226厘米，大家用計算器重新來算一算，這6個人的平均身高是多少？（171厘米）這個171厘米是幾個人的平均身高？

生：6個。

師：我們來看看這5個小朋友，有沒有哪個的身高達到這個平均數？（沒有）那這個時候這個平均數還平均嗎？

生1：不平均。

生2：平均。

師：一會不平均一會平均，看來問題有點復雜，主要是誰造成的？下課之后大家去研究一下，遇到這種情況該怎么辦。

[賞析]平均數是“敏感”的，每一名隊員的身高都會對平均數產生影響，增加（減少）隊員，平均數亦隨之發生變化。通過對“虛擬球隊”平均身高的測算，體會極端數據對平均數的影響，讓學生初步感悟統計結論沒有“對錯”之分，只有“好不好”“合理不合理”之分。平均數看上去很合理，可有時又覺得不太合理，因為平均數的大小極易受極端數據的影響。

（作者單位：江蘇省海安市明道小學教育集團，江蘇，海安226600）