函數圖象的幾個考向

廖浩偉

函數圖象是表示函數的方法之一，也是中考命題的熱點，結合幾則例題，探討函數圖象的幾個考向，即根據具體問題畫出函數圖象，根據函數圖象獲取信息解決問題，以及動點問題的函數圖象，以幫助學生掌握函數圖象的處理方法，突破函數圖象難點.

1 根據具體問題畫出函數圖象

根據具體問題畫函數圖象，首先要找出函數圖象的起點、拐點、終點，它們決定了函數圖象的范圍與方向；其次要找出每兩“點”之間的函數關系屬于一次函數、二次函數還是反比例函數，它決定了函數圖象的形狀；最后用平滑的曲線按自變量由小到大的順序，將關鍵點連接起來.

例1體育課上老師布置學生練習往返跑，小剛去時以4 m/s的平均速度跑完，回來時以6 m/s的平均速度跑回起點，速度與時間的變化關系如圖1.

（1）從起點到終點的路程是多少？

（2）在圖2中畫出小剛跑步中，離終點距離s（單位：m）與時間t（單位：s）之間的大致圖象.

解析：（1）從橫坐標可以看出，小剛去時所用時間為12 s，這段時間小剛的速度為4 m/s，所以從起點到終點的路程為4×12=48（m）；

（2）小剛奔跑時間為0時，離終點距離為48 m，此時點的坐標為（0，48）;

當小剛到達終點時，奔跑時間為12 s，離終點距離為0 m，此時點的坐標為（12，0）;當小剛回到起點時，奔跑時間為20 s，與終點的距離為48 m，此時點的坐標為（20，48）.所畫圖象如圖3所示.

評注：本題中畫出了兩個函數圖象，第一個圖象反映的是奔跑速度與時間之間的關系，第二個圖象反映的是小剛到終點距離和時間之間的關系，雖然所講的都是小剛練習往返跑的事情，但是因為變量不同，函數圖象也截然不同，所以畫函數圖象時指明橫、縱坐標表示的量很重要.

2 獲取函數圖象信息解決問題

對于函數圖象，一方面要抓住函數圖象的起點、拐點、終點及兩函數圖象的交點，兩函數圖象交點說明此時函數值相等，在同一坐標系內，在上方的函數圖象，函數值較大，在下方的函數圖象函數值較小；另一方面要弄清楚坐標系中橫、縱坐標表示的量，這樣才能與題中的文字敘述銜接起來.

例2某車間的甲、乙兩名工人分別同時生產同種零件，在開始生產的前2個小時為生產磨合期，2個小時后有一人停工一段時間對設備進行改良升級，以提升生產效率，另一人進入正常的生產模式.他們每人生產的零件總數y（單位：個）與生產時間t（單位：h）的關系如圖4所示.根據圖象回答：

（1）在生產過程中，哪位工人對設備進行改良升級，停止生產多長時間？

（2）當t為多少時，甲、乙所生產的零件個數第一次相等？甲、乙中，誰先完成一天的生產任務？

（3）設備改良升級后每小時生產零件的個數是多少？與另一工人的正常生產速度相比每小時多生產幾個？

解析：（1）由圖象可知，甲有一段圖象是水平的，表示在這段時間內生產的零件沒有增加，所以在生產的過程中，甲進行了改良，停止生產的時間5-2=3（h）.

（2）由圖象可知，當t=3時，甲與乙的函數圖象第一次相交于一點，所以當t=3時，甲和乙第一次生產零件的個數相同，均為10個.由圖象可知，甲完成任務用時7 h，乙完成任務用時8 h，所以甲、乙中，甲先完成一天的生產任務.

（3）由圖象可知，設備改良升級后，甲共生產的零件數為40-10=30（個），所用時間為7-5=2（h），所以設備改良升級后甲每小時生產零件的個數是30÷2=15（個）；乙進入正常生產后，共生產了36個零件，所用時間為8-2=6（h），所以每小時生產零件的個數是36÷6=6（個）.因此，改良后，甲每小時比乙多生產15-6=9（個）.

評注：對于函數圖象，水平線表示自變量增加而函數值沒變;從左往右看，上升線表示函數值隨自變量的增大而增大；下降線表示函數值隨自變量的增大而減小.

3 動點問題的函數圖象

動點問題首先要確定動點的運動路徑和運動方向，其次要弄清運動速度，一般以運動時間為自變量，以某條線段的長或圖形的面積為因變量，根據因變量的變化情況，常以拐點為分界點，動點的運動路徑可分為幾個階段，在不同的階段自變量與因變量會呈現不同的函數關系，也就是在不同的自變量范圍內，函數圖象在變化.

例3如圖5所示，△ABC中，AC=6 cm，AB=BC=5 cm，點P從點B處出發，沿B→C→A路徑以1 cm/s的速度勻速運動至點A，設BP長度為y cm，運動時間為x s.校數學研究小組嘗試進行函數y隨自變量x的變化而變化的規律的探究.以下是數學研究小組的探究過程，請補充完整：

（1）通過取點，畫圖，測量，得到以下y與x的幾組數值，如表1所示：

要求：填充表格中空白處的數值（結果保留一位小數）；

（2）在平面直角坐標系中，描出以補全后的表中各組對應值為坐標的點，在圖6中畫出該函數的圖象；

（3）基于作出的函數圖象，解決如下問題：當x約為時，BP=CP.

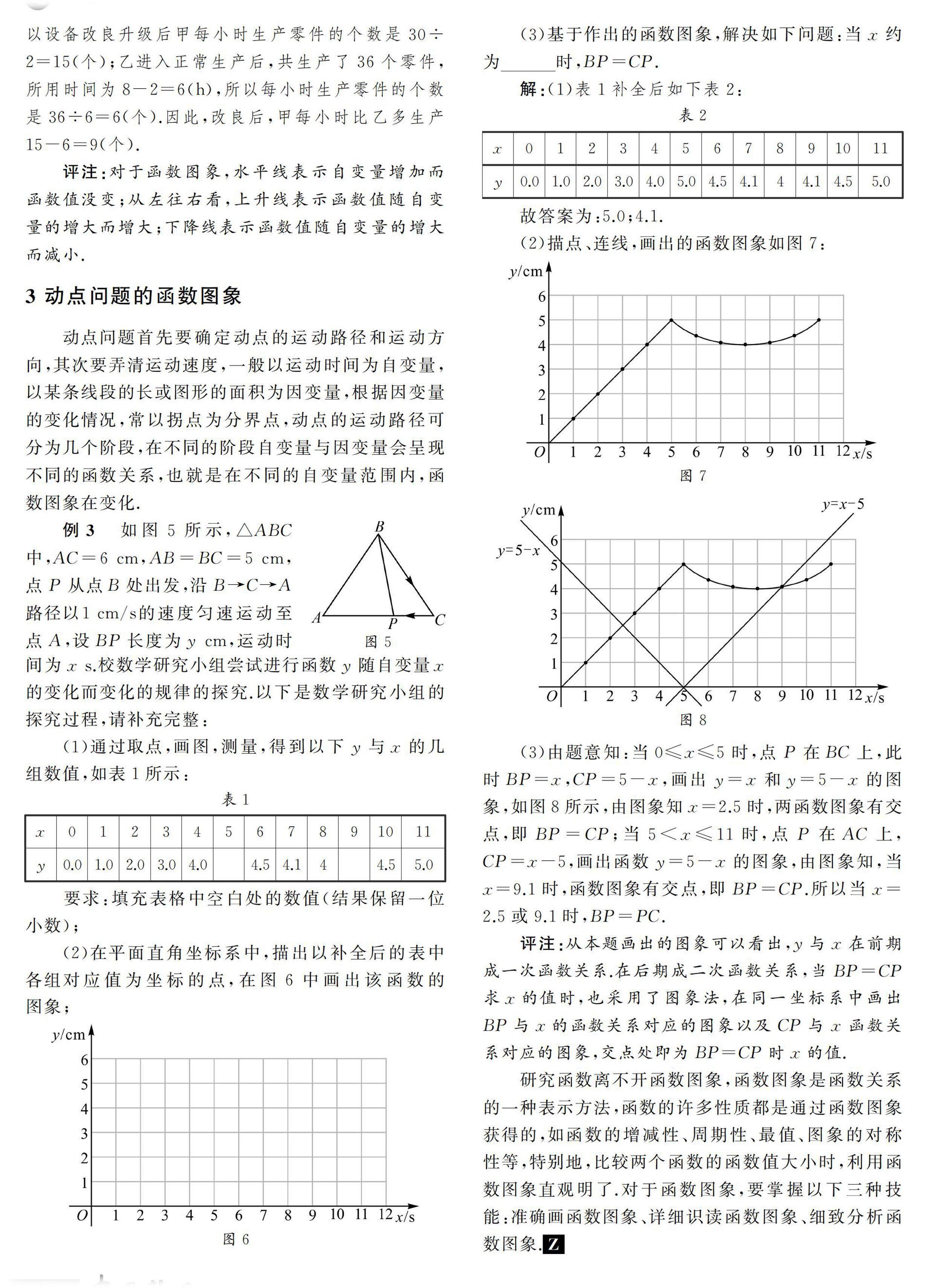
解：（1）表1補全后如下表2：

故答案為：5.0；4.1.

（2）描點、連線，畫出的函數圖象如圖7：

（3）由題意知：當0≤x≤5時，點P在BC上，此時BP=x，CP=5-x，畫出y=x和y=5-x的圖象，如圖8所示，由圖象知x=2.5時，兩函數圖象有交點，即BP=CP；當5＜x≤11時，點P在AC上，CP=x-5，畫出函數y=5-x的圖象，由圖象知，當x=9.1時，函數圖象有交點，即BP=CP.所以當x=2.5或9.1時，BP=PC.

評注：從本題畫出的圖象可以看出，y與x在前期成一次函數關系.在后期成二次函數關系，當BP=CP求x的值時，也采用了圖象法，在同一坐標系中畫出BP與x的函數關系對應的圖象以及CP與x函數關系對應的圖象，交點處即為BP=CP時x的值.

研究函數離不開函數圖象，函數圖象是函數關系的一種表示方法，函數的許多性質都是通過函數圖象獲得的，如函數的增減性、周期性、最值、圖象的對稱性等，特別地，比較兩個函數的函數值大小時，利用函數圖象直觀明了.對于函數圖象，要掌握以下三種技能：準確畫函數圖象、詳細識讀函數圖象、細致分析函數圖象.