“教-學-評”一體化學習進程設計與實施

李雪萊

學習進程指學生達成學習目標需要經歷的學習過程。學習進程設計可以指向整個學段教學過程的規劃，可以指向整個單元教學主題活動的規劃，還可以指向某個課時教學環節的規劃。本文以《擺一擺，想一想》數學綜合實踐活動課為例，探究“教-學-評”一體化的學習進程設計與實施。

一、明晰教學目標

《擺一擺，想一想》是綜合與實踐學習領域的內容，旨在引導學生通過把一定數量的圓片分別擺在數位表的十位和個位上，得到不同的數的活動過程，進一步鞏固100以內數的認識，體悟“位值制”思想。一年級學生剛接觸100以內的數，認識了數位順序和數的組成，有較好的知識基礎與學習經驗。但學生處在初步體驗位值制思想的階段，有序思考能力不強，在擺一擺的過程中會出現遺漏的情況；缺少數學基本活動經驗，不能準確表達和記錄活動結果；自主探究規律的意識不強。這些是本節課教學要面臨的困難。

課程標準明確指出，綜合與實踐主題活動的目標表述應該向學生傳達清楚具體的活動要求，便于學生明確所要完成的任務及任務涉及的各方面指標，進而在清晰的目標下制訂方案，開展解決問題的系列活動。

綜合《擺一擺，想一想》的課程目標、學段目標和單元目標，筆者確定了“①通過在數位表上擺圓片的活動，加深對100以內數的認識，進一步鞏固數位和位值的概念；②通過探究圓片個數與所擺出的數的個數之間的關系，學會發現規律；③能用發現的規律解決一些簡單的實際問題，培養初步的歸納能力；④在自主探索中體會有序思考的重要性，在合作交流中養成傾聽、有條理地表達想法的習慣和意識，體會數學與現實生活的聯系”的課時教學目標，并明確了“在活動中鞏固數位和位值思想，加深對100以內數的認識”的教學重點和“在活動中感受有序思考的價值，初步培養歸納能力、形象思維能力和抽象思維能力”的教學難點。

二、匹配評價方案

筆者將教學目標與表現性評價任務、終結性評價水平劃分相匹配，明確評價方案。例如，教學目標①對應的表現性評價目標是“學生在擺圓片的活動中，小組交流合作，根據自己擺的結果完成簡單表格的記錄”，相應的終結性評價水平處于理解層次。教學目標④對應的表現性評價目標是“學生經歷完整的發現、提出、分析、解決問題的過程，并能將有序思考的數學思想應用到其他數學問題中”，相應的終結性評價水平處于體驗、應用層次。

在學習進程的設計與實施過程中，評價伴隨始終，在活動過程中，教師要進行多維、多元、多樣化的評價：活動過程評價與學習成果評價并重，自評與互評并行，操作表現的評價和傾聽表現的評價并舉。

三、設計學習活動

專題學習活動1：玩中生成問題

對一年級學生來說，感受數學的樂趣非常重要，因此，筆者設計了“摸圓片，比大小”的游戲，讓學生在游戲中產生“同樣多的圓片怎樣擺出不同的數”的疑問，從而復習了數位與位值的概念。學生發現同一個圓片擺在不同的數位上表示的數不同，并且理解了數位表的用途。

專題學習活動2：擺中引發思考

筆者引導學生嘗試用圓片在數位表上擺出不同的數，把結果記錄在簡單的統計表中，進行有序思考。

第一次，嘗試擺，運用知識。學生在筆者指導下用數位和數值的知識擺出2個圓片的所有組數情況，并將結果完整記錄在表格內。

第二次，探究擺，展示發現。學生通過用3個圓片擺出并讀出不同的數，發現可以通過思考數的組成，不重復、不遺漏地擺出所有答案，便于按順序記錄結果。小組內學生在逐個移動圓片的過程中初步體會了有序思考，認識到擺數可以從大到小擺，也可以從小到大擺。

第三次，運用擺，感悟規律。借助第二次擺發現的竅門，學生用4個、5個圓片分別擺出不同的數，有的學生甚至能直接記錄擺的結果。通過靜心觀察，學生發現、總結其中蘊含的規律：擺出的不同的數的個數比圓片的個數多1。

第四次，不用擺，遷移規律。最后，學生不必擺圓片，就綜合運用所發現的規律，直接說出用6，7，8，9個圓片能擺出哪些數。

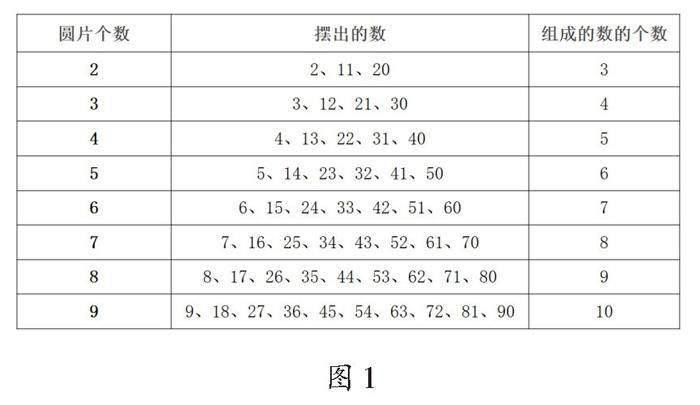
活動過程中，學生從依托學具操作到逐步擺脫學具，他們在觀察、比較、分析中習得了學習方法，提升了抽象思維水平，得到了數學規律：把一定數量的圓片分別擺在數位表的十位和個位上，組成的數的個數比圓片的個數多1（如圖1所示）。

專題學習活動3：辨中積累經驗

筆者通過教材中的形象小機器人聰聰設置闖關游戲情境，讓學生在學中玩，在玩中學，積極主動地運用規律解決問題。

闖關1：由形到數驗證規律。“小芳用6個圓片擺出了下面這些數，你們讀一讀，想一想，說一說，她擺得對嗎？你們有什么發現？”學生發現6個圓片應該擺出7個數字，小芳只擺出了6個數字（60，51， 42， 24， 15， 6），還差數字33。

闖關2：由數到形應用規律。“老師給大家一些數，8，17，26，35，44，53，62，71，80，你們知道這些數是通過擺幾個圓片表示出來的嗎？你們是怎么知道的？”學生發現9個數字，需要8個圓片才能擺出來，并進行了操作驗證。

闖關3：數形結合拓展規律。筆者出示□、□、□、□、□、□、□、□，并引導：“現在一個數都不提供，用一個□表示一個數，那么方框中的這些數是用幾個圓片表示出來的？其中最大的數是多少？最小的數是多少？”學生發現這些數是用7個圓片表示出來的，最大的數是70，最小的數是7，并得出規律：用了幾個圓片，最大的數就是幾十，最小的數就是幾。

專題學習活動4：聯中拓展能力

在本節課的最后，筆者出示百數表，使教學重新回到數的組成與認識中。筆者引導學生思考：當圓片的個數繼續增多時，所擺出來的數還有這樣的規律嗎？10個圓片是什么情況？11個、12個圓片呢？請你結合記錄表和百數表（如圖2所示）思考。

學生通過擺圓片以及觀察百數表，發現圓片數量超過10個時，規律已經不同。以10個圓片為例，會出現個位上或十位上擺10個圓片的情況，這樣的數是擺不出來也讀不出來的，因為個位和十位上的數都必須小于10。斜著看百數表，學生發現能得到所有“個位和十位上數字相加之和是10”的兩位數，這才是可以用10個圓片擺出的數。這一學習活動溝通了百數表與所擺出的數之間的關系，讓學生直觀理解了100以內數的特點。

（作者單位：武漢市漢陽區墨水湖小學）

（本文為“教-學-評”一體化主題征文獲獎作品）

責任編輯 ?孫愛蓉