逆向教學思維下的小學數學“教—學—評”一體化教學設計

作者簡介：袁芳（1974—），女，漢族，甘肅蘭州人，大專，副高級職稱，研究方向：小學數學教育教學。

常規教學思維下的小學數學教學關注教學任務、教學活動的設計，忽視學生發展需求和教學評價的重要性，在一定程度上影響學生對自身學習情況的客觀認識，繼而影響教學效果。教師教學、學生學習、教學評價三項教學工作是不可分割的，教師只有認識到這一點，并根據具體教學需要設計教學方案，才能保證學生在教學中取得豐富收獲。教師有必要逆轉教學思維，基于實際教學情況反思教學要達到怎樣的目的、怎樣判斷學生是否實現了教學目標、如何引導學生實現教學目標等，并基于逆向教學思維設計“教—學—評”一體化教學方案，使教師教學、學生學習、教學評價三者成為一個有機的整體，為提高學生的數學課程學習效果創造良好的教學環境。為此，本文以四年級下冊“三角形”單元教學為例，探究逆向教學思維下的小學數學“教—學—評”一體化教學設計策略。

一、目標設計

為了實現小學數學“教—學—評”一體化，教學目標必須有以下特點：（1）可以確定學生應當學習哪些內容；（2）可以確定學生對教學內容的接受程度；（3）所整理的教學內容是可以傳授給學生的；（4）教學目標具有確定性，可以作為評價任務的設計參考。由此，在“三角形”單元教學目標設計階段，教師應做好課程標準、教材內容、學生學情分析工作，并綜合分析結果設定教學目標。

（一）分析課程標準

《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）針對“三角形”的學業要求有：（1）能直觀描述三角形的特征；（2）知道三角形任意兩邊之和大于第三邊；（3）會根據角的特征對三角形分類，認識直角三角形、銳角三角形和鈍角三角形；（4）能根據邊的相等關系，認識等腰三角形和等邊三角形；（5）知道三角形的內角和是180°；（6）探索并掌握多邊形的內角和公式。

基于新課標的分析結果，教師可以明確學生在“三角形”教學中應當學習的具體內容。

（二）教材分析

“三角形”單元學習內容的編排建立在“平行四邊形和梯形”等內容基礎上，對三角形的穩定性、三角形三邊關系、三角形分類、三角形內角和及多邊形內角和展開介紹，一方面用文字、數學符號概述有關三角形的數學規律，另一方面借助圖形、案例進行說明，為學生后續學習“多邊形的面積”“長方體與正方體”等單元內容奠定基礎。

基于教材內容分析結果，教師整理出可以傳授給學生的重要知識點。

（三）學情分析

四年級學生經過兩個學段的學習，對三角形已經有了直觀認識，能夠從平面圖形中分辨出三角形，且掌握了角度測量、邊長測量、數學計算的方法與技巧。但是，此階段的學生對三角形的分類、三角形內角和規律缺乏認識。

基于學情分析結果，教師可以確定學生能夠接受圖形的觀察、圖形規律的探究等教學內容，有能力基于已掌握的圖形觀察、測量、研究方法探究三角形的性質、三邊關系等。

（四）教學目標

1.明確三角形的穩定性，知道三角形兩邊之和大于第三邊，知道三角形內角和為180°。

2.學會根據角的特點區分銳角三角形、直角三角形、鈍角三角形；學會根據邊的特點區分等腰三角形、等邊三角形。

3.學會應用拼擺、猜想、設計等方法探究三角形特征，并由此總結出圖形研究的通性通法，提高觀察圖形與動手操作能力。

二、評價任務設計

逆向教學思維下的“教—學—評”一體化教學設計中，教師在明確學生應達成怎樣的學習目標以后，還應設計判斷學生是否達成學習目標的評價任務，確定學生的發展情況，并根據評價結果調整教學細節，改進教師教學與學生學習的方式。評價任務的設計要參考教學目標，還要聯系評價方法、評價結果呈現與反饋等要素。逆向教學思維下的評價任務設計思路如下（見表1）。

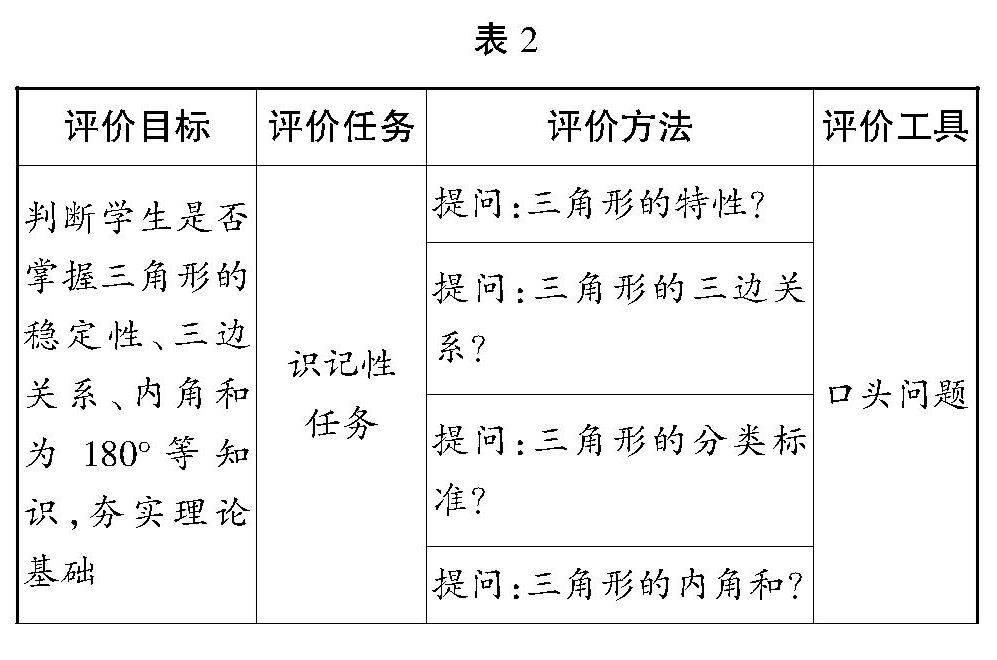
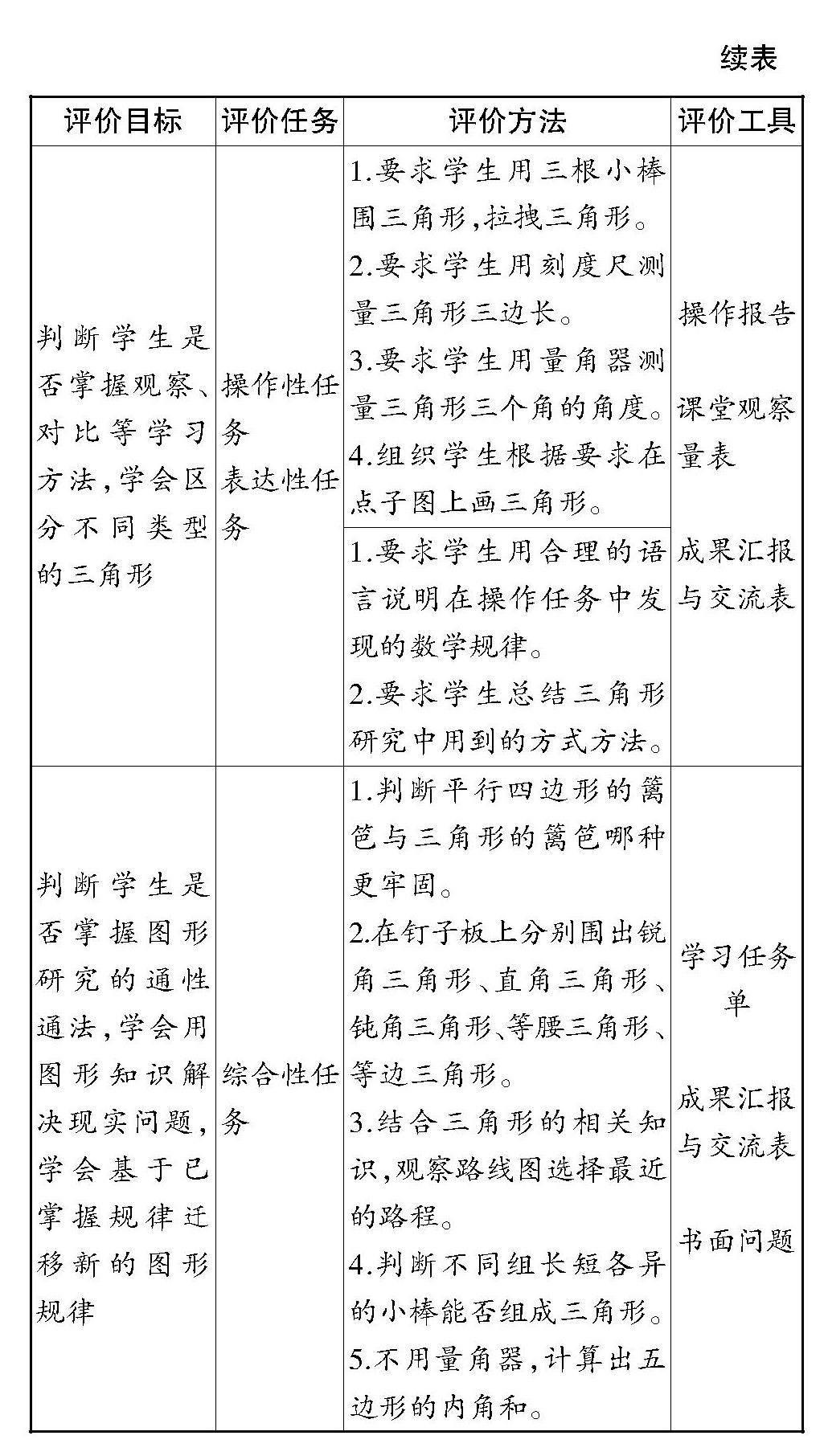
以四年級下冊“三角形”單元教學評價任務設計為例，教師可設計如下評價任務（見表2）。

三、教學活動設計

逆向教學思維下的“教—學—評”一體化教學設計中，教師需要思考如下問題：哪些學習體驗和教學能夠使學生達到預期的學習目標？哪種方式可以使學生對教學內容產生興趣？怎樣教學可以驅動學生分享自身的學習觀點？什么樣的活動可以使學生自主參與到數學規律的探究過程中？基于上述問題，教師再結合教學目標、評價任務設計，能夠使學生達成學習目標的教學活動，確保教師教學、學生學習與評價反饋成為有機的整體。

以四年級下冊“三角形”單元教學為例，教師可以先后設計對比、討論、分類、操作、練習教學活動，并將教學評價應用到各活動當中，及時與學生交流、反饋，指導學生先了解三角形具有穩定性、三角形的三邊關系、三角形的內角和等知識，促進學生內化、吸收，提高單元教學效果。具體設計內容如下所示。

（一）對比活動

結合教材，組織學生對比觀察圖片內容（見圖1），引導學生初步認識三角形。

教師指導學生觀察空調外機、塔吊、電線桿上的三角形，引導其分析：三角形在這些事物中起到什么作用，如果將三角形換成平行四邊形，是否還可起支撐、穩定作用？經觀察對比，學生明確：三角形具有穩定性。在此期間，教師觀察學生是否積極參與到圖片觀察、對比活動當中，能否快速辨別圖片中的三角形，是否能基于“平行四邊形不穩定性”遷移“三角形具有穩定性”這一知識點，判斷學生是否掌握三角形的性質，是否可以開展后續教學活動。

（二）討論活動

圍繞“三角形任意兩邊的和大于第三邊”這一重點知識，教師可結合生活案例出示圖片（見圖2），提出問題，組織討論，引導學生探究。

師：小明由家至商場共有三條路，哪條路最近？

生：最中間的那條路最近，因為兩點之間，線段最短。

師：觀察圖形，你能推斷出什么？

生：三角形的兩邊之和一定大于第三邊。

教師圍繞圖片組織討論，激活學生的直觀思維，使其在觀察的過程中發現幾何規律，完成對“三角形”教學重點的初步探索。在此活動中，教師觀察學生是否主動參與討論，是否采取畫草圖、用刻度尺測量等探究學習行為，是否在對比數據的過程中總結數學規律等，及時做出評價反饋，端正學生的探究行為，使其學會基于直觀現象、客觀數據分析幾何圖形特征，形成數學探究能力。

（三）分類活動

為使學生明確三角形的種類，認識到銳角三角形、直角三角形、鈍角三角形與三角形的從屬關系，教師可設計分類活動，為學生提供多種類型的三角形，指導其確定分類依據并進行分類。

1.從邊的角度出發，發現無法根據邊的特征分類。

2.從角的角度出發，發現有的三角形三個角都是銳角，有的三角形有一個鈍角，兩個銳角；有的三角形有一個直角，兩個銳角，得出以下結論：

（1）三個角都是銳角的三角形叫作銳角三角形；

（2）有一個角是直角的三角形叫作直角三角形；

（3）有一個角是鈍角的三角形叫作鈍角三角形。

3.將所有三角形視作一個整體，銳角、直角、鈍角三角形是三角形的一部分。

教師觀察學生的分類過程，對其分類行為、結果作出評價，判斷學生是否明確三角形的分類依據，指出學生分類學習表現得優異之處及不足，鞏固教學成果。

（四）操作活動

教師布置操作任務，同時將教學內容蘊藏于任務當中，指導學生在完成任務的同時探索數學規律。如：應用量角器測量三角形三個內角，將數據記錄下來，總結規律。

1.直角三角形：1個角為90°，另外兩個角為40°、50°，三個角度之和為180°。

2.鈍角三角形：1個角為100°，另外兩個角為25°、55°，三個角度之和為180°。

3.銳角三角形：三個角分別為45°、75°、60°，三個角度之和為180°。

結論：三角形內角和為180°。

教師布置操作任務，驅動學生參與數學探究，使其在測量角度、計算角度之和的過程中發現三角形內角和為180°的規律，鍛煉學生操作能力的同時培養其數學觀念。教師可在此過程中觀察學生是否主動對各數據進行計算、分析，能否獨立抽象數學規律等，并給出教學評價，指導學生調整操作學習行為。

綜上所述，逆向教學思維下，教師重點圍繞“學生應在學習中達成怎樣的目標”“怎樣判斷學生是否達成學習目標”“怎樣使學生達成學習目標”等問題梳理教學思路，并根據實際教學需要設計具體評價任務及教學活動，確保教師教學、學生學習、教學評價反饋三項工作有機結合。

（作者單位：甘肅省永登縣仁愛光彩小學）

編輯：陳鮮艷