考慮周期折減的結構彈性時程分析調整方法

吳克川 陶忠 潘文 蘭香 余文正 張龍飛

摘要：針對結構彈性時程分析時無法考慮周期折減的問題展開研究，通過對比結構時程分析的過程中，地震波的選取是否考慮周期折減的差異，提出采用增大系數放大時程分析法輸入地震波有效峰值加速度以及地震響應；考慮彈性時程分析過程中，周期折減對結構地震作用的增大效應。理論分析增大系數取值的影響因素，并基于單自由度體系對比兩種調整方法的效果及差異，采用實際算例以驗證所提出彈性時程分析中考慮周期折減調整方法的有效性。結果表明：增大系數的取值與周期折減系數、結構自振周期及場地特征周期等因素有關;對于單自由度體系，兩種調整方法具有完全相同的調整效果;按文章提出方法考慮周期折減的算例結構，彈性時程分析所得各樓層地震剪力及層間位移角與考慮周期折減的反應譜（CQC）計算結果均較為接近。

關鍵詞：彈性時程分析; 周期折減; 增大系數; 反應譜; 地震波調整

中圖分類號： TU352.1;P315.97????? 文獻標志碼：A?? 文章編號： 1000-0844（2024）03-0548-10

DOI：10.20000/j.1000-0844.20220529002

Adjustment method for elastic time-history analysis of structures considering period reduction

WU Kechuan1， TAO Zhong2， PAN Wen2， LAN Xiang1， YU Wenzheng1， ZHANG Longfei1

（1. College of Architecture and Civil Engineering， Kunming University， Kunming 650214， Yunnan， China;2. Institute of Civil Engineering， Kunming University of Science and Technology， Kunming 650500， Yunnan， China）

Abstract：?The problem that the period reduction cannot be considered in a structural time-history analysis was studied. Structural time-history analyses considering and neglecting the period reduction were compared， and then the amplification coefficient was proposed to amplify the effective peak acceleration of the input ground motion and the seismic response in time-history analysis to consider the amplification effect of period reduction on the structural seismic response in elastic time-history analysis. The influences of involved parameters on the amplification coefficient were studied theoretically. Then， the adjustment effects and differences between the two adjustment methods were compared on the basis of the single-degree-of-freedom system. Moreover， an engineering example was used to verify the effectiveness of the proposed methods considering period reduction in the elastic time-history analysis. The results show that the value of the amplification coefficient is related to the period reduction coefficient， the natural vibration period of the structure， and the characteristic period of the site. For the single-degree-of-freedom system， the two adjustment methods have identical adjustment effects. The seismic shear force and story drift ratio of each floor of the example structure obtained using the elastic time-history analysis are near those calculated by the response spectrum considering the period reduction.

Keywords：elastic time-history analysis; period reduction; amplification coefficient; response spectrum; seismic wave adjustment

0 引言

振型分解反應譜法［1］目前廣泛應用于建筑結構地震作用的計算，該方法是一種基于彈性理論的“偽動力”方法。時程分析法［2］可計算結構在任一時刻的地震反應，并能對結構構件的損傷過程進行詳細的數值模擬。許多地震多發國家及地區已將時程分析法納入抗震設計規范，并將該方法作為不規則復雜結構、超限高層結構以及特殊重要結構靜力計算的必要補充［3］。自1989年起，我國《建筑抗震設計規范（GBJ 11—1989）》［4］開始將時程分析法作為振型分解反應譜法的補充計算手段，并對時程分析輸入地震波的選取要求作出了明確規定：彈性時程分析時，選取的每條時程曲線計算得到的結構基底剪力不應小于振型分解反應譜法計算結果的65％，各時程曲線計算得到的結構基底剪力的平均值不應小于振型分解反應譜法計算結果的80％。

由于當前國內的主流結構設計軟件PKPM及YJK等在建立結構計算模型時并未真實建立非承重墻單元，而是通過折減結構基本自振周期的方式考慮其剛度貢獻，即采用振型分解反應譜法計算出的地震力為結構周期折減后的地震力；且目前的商用結構設計和分析軟件（SAP2000、ETABS、Midas等）在彈性時程分析的過程中，由于時程分析自身算法的原因而無法考慮結構周期折減這一因素［5-6］，并且規范要求用于時程分析的地震波計算所得基底剪力與反應譜計算得到的基底剪力需滿足相應的誤差要求，兩者間存在并非同一自振周期對應地震動進行比較的矛盾，即在選取地震波的過程中是否考慮目標反應譜周期折減的問題。

目前，國內外關于彈性時程分析過程中如何考慮結構周期折減的研究較少［7-8］，已有的少數研究也僅指出采用時程分析法計算結構地震作用效應時，應當考慮非承重墻的剛度貢獻［9］，但并未給出具體的考慮周期折減的方法。基于此，本文對選波過程中是否考慮目標反應譜周期折減的差異進行了對比，基于對比分析結果給出考慮相應周期折減的結構彈性時程分析調整方法，并采用工程案例驗證分析所提出調整方法的有效性，以供工程設計參考。

1 目標反應譜周期是否折減的差異

1.1 目標反應譜考慮周期折減

在選取地震波的過程中，當考慮結構非承重墻的剛度貢獻，即考慮結構周期折減系數的影響時，由前文分析可知，由于基于地震波的彈性時程分析法無法考慮該因素，因此，選波時將結構折減后周期T1對應的規范反應譜地震影響系數α1［圖1（a）中C點］與結構折減前周期T0對應的地震波反應譜地震影響系數α0［圖1（a）中B點］進行比較，當α1與α0的取值較為接近時，則可通過比較結構的基底剪力得到滿足規范要求的地震波。但此時注意到，地震波反應譜曲線相較于規范反應譜曲線有向右“漂移”的趨勢，這是因為在比較地震影響系數時，采用不同周期點（周期折減前與折減后）對應值進行比較，這將導致所選取的地震波與規范反應譜的頻譜成分有較大差異［如圖1（a）］，即所選取的地震波雖然計算得到的基底剪力與振型分解反應譜法的結果接近，但并不符合地震波選取的本質條件，也就是說，考慮目標反應譜周期折減后選取得到的地震波在場地類別以及地震分組等方面并不能很好地與規范要求進行匹配。圖1為按照上述方法選取的地震波對應的加速度反應譜、位移反應譜、速度反應譜與相應的規范反應譜曲線的對比。從圖1中可以看出，各類譜曲線與規范反應譜均有較大的差異，這也在一定程度上說明考慮目標反應譜周期折減的選波方法雖能較好地反映非承重墻對結構地震作用的增大效應，但其合理性也有待商榷［10］。

1.2 目標反應譜不考慮周期折減

如果在選取地震波的過程中不考慮結構周期折減系數的影響，即地震影響系數采用同一周期（T0）對應值進行比較，此時選取得到的地震波反應譜曲線與規范反應譜曲線擬合程度較高，如圖2所示。從圖中也不難看出，由于未對結構自振周期進行折減，采用上述方法選取的地震波進行結構時程分析時，將低估結構的地震需求，從而使結構在地震作用下的各項性能指標驗算結果不夠可靠［11］，這主要是由于結構自振周期的折減與否對地震影響系數的取值有較大的影響。因此，按不考慮目標反應譜周期折減的方法選擇的地震波雖在頻譜特性及有效峰值等方面能較好地與規范反應譜進行匹配，但并不能真實地估計和考慮非承重墻對結構地震需求的增大作用。

2 考慮周期折減的時程分析調整方法

通過前文結構時程分析選波過程中是否考慮周期折減的差異性對比容易看出，既要滿足《建筑抗震設計規范（GB 50011—2010）》（簡稱《抗規》）的選波要求，又要能夠考慮填充墻對結構地震需求的影響，可通過選取與目標反應譜頻譜特性相匹配的地震波，并采用相應的方法合理調整地震波輸入強度或調整時程分析輸出結果。基于該原則，提出調整地震波有效峰值加速度及調整時程分析計算所得地震反應力的方法來考慮周期折減對結構抗震需求的增大作用，即：（1）根據周期折減系數的取值調整輸入地震波的有效峰值加速度;（2）根據周期折減系數的取值調整彈性時程分析計算結果。周期折減系數的具體取值可根據結構所采用的結構體系及填充墻類型（參考文獻［12-14］）進行確定。

2.1 調整地震波有效峰值加速度（方法1）

結構自振周期的折減程度將直接影響反應譜曲線的地震影響系數取值［15］，也即影響結構地震反應力計算結果的大小。為考慮周期折減對結構地震需求的增大作用，文中建議在時程分析過程中，根據周期折減系數R的取值調整頻譜特性與目標反應譜匹配的地震波的有效峰值加速度，即將《抗規》中規定的時程分析有效峰值加速度EPA乘以增大系數β后再進行彈性時程分析。不難看出，β取值的合理性決定著調整結果的合理性。本文建議β的取值為目標反應譜折減后周期T1對應地震影響系數α1與折減前周期T0對應地震影響系數α0之比：

β=α1α0 （1）

將《抗規》中各周期范圍內地震影響系數計算公式代入式（1）可得出：

β=1，T1∈［0.1，Tg］，T0∈［0.1，Tg］T0Tgγ，T1∈［0.1，Tg］，T0∈［Tg，5Tg］1Rγ，T1∈［Tg，5Tg］，T0∈［Tg，5Tg］（Tg）γη2（R·T0）γ［η20.2γ-η1（T0-5Tg）］，T1∈［Tg，5Tg］，T0∈［5Tg，6］［η20.2γ-η1（RT0-5Tg）］［η20.2γ-η1（T0-5Tg）］，T1∈［5Tg，6］，T0∈［5Tg，6］ （2）

式中：Tg為結構所在場地特征周期;η1為規范反應譜下降斜率調整系數;η2為阻尼調整系數;γ為衰減指數。

圖3為式（2）中結構折減前周期與折減后周期處于不同范圍時，增大系數β與周期折減系數R的關系曲線。從圖3中可以看出：（1）當周期折減系數R取值相同的情況下，T0及T1處于［Tg，5Tg］時，增大系數β取得最大值;（2）當T1處于［0.1，Tg］，T0處于［0.1，Tg］或處于［Tg，5Tg］時，增大系數β的取值不隨折減系數R的變化而改變，為常數值;（3）當T0及T1處于［Tg，6］時，增大系數β的取值隨折減系數R的增加而減小。

圖4為式（2）中周期折減系數R取定值時，增大系數β隨結構自振周期T0的變化關系。從圖中可以看出：（1）當T0及T1處于［0.1，Tg］或T0及T1處于［Tg，5Tg］時，增大系數β的取值不隨結構自振周期的變化而改變;（2）當T0處于［Tg，5Tg］，T1處于［0.1，Tg］或T0及T1處于［5Tg，6］時，增大系數β的取值隨結構自振周期的增加而增大;（3）當T0處于［5Tg，6］，T1處于［Tg，5Tg］時，增大系數β的取值隨結構自振周期的增加而減小。

值得注意的是，對于多自由度結構體系，上述增大系數β應考慮結構滿足有效參與質量系數所要求的前n階振型所對應自振周期的影響，即應考慮結構各主要周期的折減對增大系數β的貢獻，且應考慮各振型的參與程度對增大系數β的取值影響。參考結構振型組合方法［16-17］，多自由度體系的等效增大系數βe建議按下式計算：

βe=∑ni=1γiγtα1iα0i2 （3）

式中：α1i ，α0i分別為結構第i階折減后周期與折減前周期對應地震影響系數（i=1～n，γi為結構第i階振型的參與系數）；γt為結構前n階振型的總參與系數。

2.2 直接調整時程分析計算結果（方法2）

文中建議的另一種考慮周期折減對結構地震需求增大作用的方法為：根據結構各階周期對應計算所得增大系數βi調整彈性時程分析中相應振型的加速度響應，即將彈性時程分析計算所得結構各階振型地震力乘以相應的增大系數βi，列于式（4），從而實現調整結構時程分析中各地震波作用下結構的總地震力。

（Fij）r=βiFij （4）

式中：（Fij）r為考慮周期折減調整后的結構第i振型第j層地震力;Fij為未經調整的結構彈性時程分析計算所得結構第i振型第j層地震力。

3 調整方法的對比

3.1 對比分析概況

上述兩種考慮自振周期折減對結構地震需求增大效應的方法有所差異：方法1通過調整彈性時程分析輸入地震波有效峰值加速度的方式間接增大結構的地震力;方法2通過直接調整彈性時程分析計算所得結構各階振型加速度的方式增大結構的地震力。兩調整方法的原理不盡相同，因此，對兩方法在不同周期折減系數取值下的調整結果進行對比分析。為便于揭示一般性規律，采用具有不同自振周期的單自由度體系（SDOF）對比兩調整方法的差異，各單自由度結構體系基本參數如表1所列。基于MATLAB編制單自由度體系彈性時程分析程序［18］，各體系分別選擇符合規范要求的7條地震波（5條天然波+2條人工波）進行地震力計算，各體系所選地震波反應譜曲線與目標反應譜曲線的對比如圖5所示。從圖5中可以看出，各地震波反應譜曲線頻譜特性與目標反應譜頻譜特性匹配程度較高，可用于驗證兩種調整方法的差異。

3.2 對比結果分析

圖6為單自由度體系SODF1、SODF2、SODF3在周期折減系數R不同取值下，增大系數β的分布情況。從圖6中可以看出，增大系數β的取值與周期折減系數、結構基本自振周期及場地特征周期等因素有關，其取值的變化規律與前文2.1節分析結果一致。

圖7為單自由度體系SODF1、SODF2、SODF3在不同周期折減系數取值下，采用調整方法1和調整方法2得到的彈性時程分析地震剪力V（地震剪力取各地震波計算結果的平均值）與考慮周期折減的反應譜計算結果的對比。從圖中可以看出：（1）對于各單自由度體系，兩調整方法計算得到的地震剪力完全一致，即采用增大地震波有效峰值加速度的方法和直接放大時程分析計算所得振型地震力的方法具有相同的調整結果;（2）各體系經過調整后的地震反應力與考慮周期折減的反應譜結果較為接近。SDOF1在周期折減系數R取值為［0.6、0.65、0.7、0.75、0.8］時，調整后結果與反應譜計算結果誤差最大，為2.5%;SDOF2在周期折減系數R取值為［0.6、0.65］時，調整后結果與反應譜計算結果誤差最大，為2.35%;SDOF3在周期折減系數R取值為［0.65、0.7］時，調整后結果與反應譜計算結果誤差最大，為0.52%，說明兩調整方法均具有較好的調整效果，且能通過調整后的結果有效反映周期折減對結構地震作用的增大效應。

4 工程實例驗證分析

4.1 工程概況

為驗證文中所提出考慮周期折減的彈性時程分析調整方法的有效性，采用某實際工程案例進行驗證分析。某鋼筋混凝土框架結構共4層，底層層高5.1 m，標準層層高3.9 m，結構總高度16.8 m，結構抗震設防烈度為7度，基本設計加速度為0.15g，地震分組為第二組，場地類別為Ⅱ類，場地特征周期Tg=0.4 s，結構固有阻尼比為5%。采用YJK（4.0版本）軟件建立上述工程案例計算模型，其中框架梁柱構件采用桿單元模擬，樓板采用彈性樓板6（殼單元）模擬，并在梁和板上施加荷載，計算模型如圖8所示，結構的動力特性如表2所列。

從表2中可以看出，結構一階振型為Y向平動，二階振型為X向平動，三階振型為豎向扭轉，當結構計算振型總階數n（結構各方向振型數量之和）≥4時，結構兩主軸方向的有效振型參與質量系數均滿足規范不小于90%的要求。

4.2 兩方法調整結果與反應譜（CQC）結果對比

基于有效峰值加速度、地震波持時以及頻譜特性，選擇符合規范要求［19］的5條天然波和2條人工波對以上結構進行多遇地震作用下的彈性時程分析，所選地震波反應譜曲線如圖9所示。主要對比分析結構在不同周期折減系數取值下以及不同計算振型總階數下兩調整方法的有效性，并與反應譜（CQC）計算結果進行比較。表3為根據式（2）計算得到的結構在不同周期折減系數取值下，各階振型對應增大系數βi分布情況，以及按式（3）計算的不同計算振型總階數n取值下，多自由度結構體系等效增大系數βe的取值情況。由表3可知，增大系數的分布規律與前文的理論分析結果一致，即增大系數的取值主要與結構周期折減系數R、結構自振周期及場地特征周期等參數有關;等效增大系數βe隨結構計算振型總階數n的增大而減小，這主要是由于結構的高階振型往往具有較小的自振周期，其范圍主要位于設計反應譜的直線上升段和平臺段，對應的增大系數取值范圍≤1。但采用方法1調整地震作用時，主要調整輸入地震波的有效峰值加速度EPA，這相當于各階振型的地震力都相應地進行了放大，然而，等效增大系數βe在較大計算振型總階數下取值更小，這也相當于“調和”了結構各階振型地震力的放大效應，后文將進一步驗證采用式（3）計算等效增大系數βe的有效性。

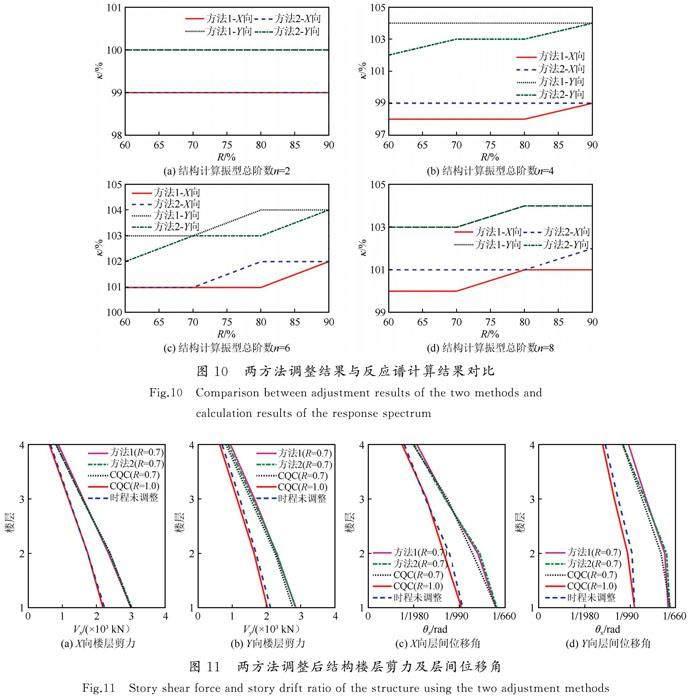
根據表3中等效增大系數βe取值及結構各階周期對應增大系數βi取值，采用方法1調整結構在不同計算振型總階數（結構各方向振型數量之和）下輸入地震波的有效峰值加速度EPA的大小，即將EPA乘以表3中相應周期折減系數及相應計算振型總階數對應的等效增大系數βe后進行彈性時程分析;采用方法2調整結構在不同計算振型總階數下彈性時程分析輸出的各階振型地震力，即將結構分析軟件計算所得第i階振型地震力乘以相應的增大系數βi后再進行振型組合。將兩調整方法得到的結構底部剪力V（取7條地震波的平均值）與相應的考慮周期折減的反應譜（CQC）計算結果進行對比，對比結果如圖10所示，采用式（5）表達對比結果：

κ=VVc （5）

式中：V為采用方法1或方法2調整后的結構底部剪力時程結果平均值;Vc為相應考慮周期折減的反應譜（CQC）計算所得底部剪力。κ的取值越接近1，相應的調整方法則具有較高的調整精度。

從圖10中可以看出，不同計算振型總階數及不同周期折減系數取值下，兩方法調整結果與反應譜（CQC）結果均較為接近，最大誤差值小于4%，這表明兩方法均具有較高的調整精度，能在彈性時程分析過程中有效考慮周期折減對結構地震作用的增大效應。特別的，當計算振型總階數n=2時，兩方法調整得到的結構兩主軸方向的底部剪力完全一致，這與前文基于單自由度體系分析得到的結論相同，當n=2時，相當于時程分析僅計算了結構在兩主軸方向的一階振型地震力，此時兩方法具有相同的調整精度，與單自由度體系分析結論一致。

4.3 兩方法調整后結構樓層剪力及位移角對比

圖11為結構計算振型總階數n=8，周期折減系數R=0.7時，采用方法1及方法2調整彈性時程分析后結構的樓層剪力（取7條地震波的平均值）及層間位移角（取7條地震波的平均值）分布情況。從圖中可以看出，采用方法1調整后，結構X向及Y向的底部剪力分別為3 010 kN、2 856 kN，最大層間位移角分別為1/715、1/704;采用方法2調整后，結構X向及Y向的底部剪力分別為3 027 kN、2 849 kN，最大層間位移角分別為1/709、1/696;考慮周期折減的反應譜（CQC）工況下，結構X向及Y向的底部剪力分別為2 998 kN、2 765 kN，最大層間位移角分別為1/693、1/712。方法1、方法2 X向及Y向底部剪力與反應譜（CQC）計算結果的誤差分別為0.41%、0.98%和3.29%、3.02%，這表明通過兩方法調整后，結構各樓層地震剪力、層間位移角與考慮周期折減的反應譜（CQC）計算結果均較為接近，也說明采用文中兩調整方法均能較好地解決目前商用結構分析軟件彈性時程分析過程中不能考慮周期折減的問題。圖11中藍色虛線為通常情況下結構分析軟件在時程分析過程中無法考慮周期折減計算得到的樓層剪力及層間位移角，X向及Y向的結果分別為2 229 kN、2 115 kN和1/966、1/951。不難看出，未考慮周期折減影響的時程計算結果不能較為真實地反映結構的地震需求［兩主軸方向底部剪力與考慮周期折減的反應譜（CQC）計算結果誤差分別為25.66%、23.52%］，從而降低了結構在地震作用下各項抗震性能指標驗算結果的可靠性，因此，建議在結構彈性時程分析過程中采用合理方法考慮周期折減對結構地震作用的增大效應。

5 結論

本文對選波過程中是否考慮目標反應譜周期折減的差異進行了對比，提出考慮周期折減的結構彈性時程分析調整方法，并運用工程算例以驗證分析所提出調整方法的有效性，得到以下結論：

（1） 時程分析選波過程中不考慮周期折減將低估結構的地震需求，考慮周期折減則所選地震波頻譜特性與目標反應譜頻譜特性匹配程度較低。

（2） 在進行結構彈性時程分析時，周期折減對地震作用的放大效應可通過文中提出的增大輸入地震波有效峰值加速度或增大輸出振型地震力的方法考慮。

（3） 增大系數β的取值與結構自振周期、周期折減系數及場地特征周期等因素有關，具體可按文中式（2）、式（3）計算。

（4） 對于單自由度體系，文中提出的兩種時程分析過程中考慮周期折減的調整方法具有相同的調整精度。

（5） 工程算例分析表明，采用方法1及方法2調整后的結構各樓層地震剪力及層間位移角與考慮周期折減的反應譜（CQC）計算結果均較為接近，最大誤差為3.29%。

參考文獻（References）

［1］ 王亞勇，程民憲，劉小弟.結構抗震時程分析法輸入地震記錄的選擇方法及其應用［J］.建筑結構，1992，22（5）：3-7.

WANG Yayong，CHENG Minxian，LIU Xiaodi.Selection method of seismic records input by structural seismic time history analysis method and its application［J］.Building Structure，1992，22（5）：3-7.

［2］ 楊溥，李英民，賴明.結構時程分析法輸入地震波的選擇控制指標［J］.土木工程學報，2000，33（6）：33-37.

YANG Pu，LI Yingmin，LAI Ming.A new method for selecting inputting waves for time-history analysis［J］.China Civil Engineering Journal，2000，33（6）：33-37.

［3］ 吳小峰，孫啟國，狄杰建，等.抗震分析反應譜法和時程分析法數值仿真比較［J］.西北地震學報，2011，33（3）：275-278，304.

WU Xiaofeng，SUN Qiguo，DI Jiejian，et al.A numerical simulation comparison between response spectrum analysis and time history analysis［J］.Northwestern Seismological Journal，2011，33（3）：275-278，304.

［4］ 國家標準抗震規范管理組.建筑抗震設計規范：GBJ 11—1989［S］.北京：中國建筑工業出版社，1989.

National Standard Seismic Code Management Group.Specifications for antiseismic construction design：GBJ 11—1989［S］.Beijing：China Architecture & Building Press，1989.

［5］ 張耀庭，劉勇，沈杰，等.結構動力時程分析的地震動選擇方法研究［J］.湖南大學學報（自然科學版），2020，47（7）：29-39.

ZHANG Yaoting，LIU Yong，SHEN Jie，et al.Research on ground motion selection method for time-history analysis of structure［J］.Journal of Hunan University （Natural Sciences），2020，47（7）：29-39.

［6］ 張銳，李宏男，王東升，等.結構時程分析中強震記錄選取研究綜述［J］.工程力學，2019，36（2）：1-16.

ZHANG Rui，LI Hongnan，WANG Dongsheng，et al.Selection and scaling of real accelerograms as input to time-history analysis of structures：a state-of-the-art review［J］.Engineering Mechanics，2019，36（2）：1-16.

［7］ 張元偉.關于彈性時程分析的一點建議［J］.建筑結構，2015，45（增刊1）：435-437.

ZHANG Yuanwei.Suggestion about the elastic time-history analysis［J］.Building Structure，2015，45（Suppl01）：435-437.

［8］ MARASCO S，CIMELLARO G P.A new energetic based ground motion selection and modification algorithm［C］//Proceedings of the 16th World Conference on Earthquake Engineering.Santiago，Chile：[s.n.]，2017.

［9］ 董銀峰，梁文舉，姚鶴彬，等.雙向地震動輸入方法對結構時程分析反應的影響［J］.建筑結構學報，2018，39（增刊1）：168-174.

DONG Yinfeng，LIANG Wenju，YAO Hebin，et al.Influence of bidirectional ground motion input method on structural time history analysis response［J］.Journal of Building Structures，2018，39（Suppl01）：168-174.

［10］ 楊志勇，黃吉鋒，邵弘.彈性與彈塑性動力時程分析方法中若干問題探討［J］.建筑結構學報，2009，30（增刊1）：213-217.

YANG Zhiyong，HUANG Jifeng，SHAO Hong.Discussion on some problems in elastic and elastic-plastic dynamic time-history analysis methods［J］.Journal of Building Structures，2009，30（Suppl01）：213-217.

［11］ KATSANOS E I，SEXTOS A G，MANOLIS G D.Selection of earthquake ground motion records：a state-of-the-art review from a structural engineering perspective［J］.Soil Dynamics and Earthquake Engineering，2010，30（4）：157-169.

［12］ 中華人民共和國住房和城鄉建設部.高層建筑混凝土結構技術規程：JGJ 3—2010［S］.北京：中國建筑工業出版社，2011.

Ministry of Housing and Urban-Rural Development of the People's Republic of China.Technical specification for concrete structures of tall building：JGJ 3—2010［S］.Beijing：China Architecture & Building Press，2011.

［13］ 陳婷婷，張敬書，金德保，等.不同種類填充墻周期折減系數取值的分析［J］.工程抗震與加固改造，2013，35（4）：48-53.

CHEN Tingting，ZHANG Jingshu，JIN Debao，et al.Analysis of period shortening factor on different infilled walls［J］.Earthquake Resistant Engineering and Retrofitting，2013，35（4）：48-53.

［14］ 蔡鳳維，金燦國.輕質填充墻對框架結構計算分析影響探討［J］.廣東土木與建筑，2020，27（6）：17-21.

CAI Fengwei，JIN Canguo.Discussion on the influence of light infiled wal on the calculation and analysis of frame structure［J］.Guangdong Architecture Civil Engineering，2020，27（6）：17-21.

［15］ BAKER J W，LEE C.An improved algorithm for selecting ground motions to match a conditional spectrum［J］.Journal of Earthquake Engineering，2018，22（4）：708-723.

［16］ 孫攀旭，楊紅.基于等效黏性阻尼模型的非比例阻尼體系反應譜CCQC法［J］.工程力學，2021，38（10）：160-172，180.

SUN Panxu，YANG Hong.A response spectrum CCQC method for non-proportionally damped systems based on equivalent viscous damping model［J］.Engineering Mechanics，2021，38（10）：160-172，180.

［17］ KURAMA Y C，FARROW K T.Ground motion scaling methods for different site conditions and structure characteristics［J］.Earthquake Engineering& Structural Dynamics，2003，32（15）：2425-2450.

［18］ KOTTKE A，RATHJE E M.A semi-automated procedure for selecting and scaling recorded earthquake motions for dynamic analysis［J］.Earthquake Spectra，2008，24（4）：911-932.

［19］ 徐天妮，杜永峰，馬守才.基于易損性的基礎隔震結構地震動選取方法研究［J］.地震工程學報，2022，44（1）：46-53.

XU Tianni，DU Yongfeng，MA Shoucai.A method of ground motion selection for base-isolated structures based on vulne-rability analysis［J］.China Earthquake Engineering Journal，2022，44（1）：46-53.

（本文編輯：任 棟）

基金項目：云南省地方高校基礎研究聯合專項項目（202101BA070001-176）;國家自然科學基金項目（52368019）;昆明學院人才引進項目（YJL19011）

第一作者簡介：吳克川（1988-），男，博士，講師，主要從事工程結構減震控制研究。E-mail：452969980@qq.com。

吳克川，陶忠，潘文，等.考慮周期折減的結構彈性時程分析調整方法［J］.地震工程學報，2024，46（3）：548-556.DOI：10.20000/j.1000-0844.20220529002

WU Kechuan，TAO Zhong，PAN Wen，et al.Adjustment method for elastic time-history analysis of structures considering period reduction［J］.China Earthquake Engineering Journal，2024，46（3）：548-556.DOI：10.20000/j.1000-0844.20220529002