增強組合差分乘積形態學濾波的軸承故障特征提取方法

徐先峰 趙衛峰 鄒浩泉 宋亞囡

收稿日期：2021-12-01

網絡出版日期：2022-04-27

基金項目：陜西省自然科學基礎研究計劃資助項目（2019JQ-678）；陜西省重點研發計劃資助項目（2021GY-098）；西安市智慧高速公路信息融合與控制重點實驗室資助項目（ZD13CG46）；長安大學中央高校基本科研業務費專項資金資助項目（300102321504，300102321501，300102321503）。

作者簡介：徐先峰（1982—），男，副教授，博士，主要從事信號處理、深度學習理論及應用和智能電網研究，（E-mail）xxf_chd@163.com。

摘要：針對滾動軸承故障信號的非線性、非平穩、強噪聲特性導致的常規時頻域特征提取方法受限問題，提出一種增強組合差分乘積形態學濾波的軸承故障特征提取方法。在分析數學形態學4種基本運算的正、負沖擊脈沖提取特性的基礎上，運用級聯、差分、乘積構造的一種新的組合差分乘積算子（combination difference multiply operator， CDMO）具備了同時提取正、負沖擊脈沖的能力，并發揮梯度乘積運算對脈沖提取更敏感的優勢，實現故障信息的充分提取。引入故障特征頻率比指標優化CDMO結構元素參數，修正待處理信號的幾何特征，提取與結構元素相匹配的信號特征信息。在CDMO濾波的基礎上，借助三階累積量切片譜技術能夠抑制高斯噪聲、突出二次耦合分量的優勢，準確提取故障特征頻率及其倍頻，增強軸承故障特征提取能力并抑制噪聲干擾。依托2種不同來源的工程實際信號并與經典故障特征提取方法對比分析，驗證了所提方法的有效性。

關鍵詞：滾動軸承；形態學濾波；三階累積量切片譜；特征提取

中圖分類號：TH113 ?????????文獻標志碼：A ?????? 文章編號：1000-582X（2024）03-096-11

滾動軸承作為機械設備的易損核心部件，對整個機械設備的穩定運行起決定性作用，研究其故障診斷方法對實際工程意義重大^[1]。滾動軸承原始振動信號具有非線性、非平穩以及噪聲干擾強的特點，且噪聲信號多呈現高斯特性^[2]，從中提取微弱故障特征是滾動軸承故障診斷的關鍵^[3]。

短時傅里葉變換、小波變換、經驗模態分解等時頻域方法可以實現軸承故障特征提取^[4-6]。何強等^[4]對軸承振動信號進行短時傅里葉變換，輸入語義卷積神經網絡（semantic convolutional neural network，SeCNN）進行故障分類，針對小樣本數據獲得了準確有效的實驗結果。但是，短時傅里葉變換無法同時對高頻和低頻信號進行有效分析。范春旸等^[5]提出一種基于小波變換結合隨機森林的故障分析模型，能選擇出對故障狀態較為重要的特征，但是，選取恰當的基函數存在困難。經驗模態分解方法也存在模式混疊、對噪聲敏感等不足^[6]。

數學形態學是一種適合于非線性、非平穩過程的抗噪聲信號處理方法，通過結構元素（structuring element，SE）修正待處理信號的幾何特征，降噪能力好，計算簡單^[7]，近年來在機械故障診斷領域得到了廣泛應用。目前，關于形態學濾波方法的研究多集中于決定故障特征提取效果的形態學算子構造與結構元素參數確定兩方面。Li等^[8]提出加權多尺度形態學梯度濾波（weighted multi-scale morphology gadient，WMMG），改進了傳統多尺度形態學濾波的特征提取能力，但其權重系數配比不易尋優，在一定程度上弱化了個別尺度作用較強的結果所包含的特征信息。Lv等^[9]將4種基本形態學算子進行平均組合差分以突出故障特征的周期性脈沖，但平均組合差分效果不及乘積運算。Li等^[10]提出一種形態學梯度乘積算子，并結合高階譜分析方法—三階累積量切片譜提取軸承故障特征，獲得了良好的效果，但僅采用開閉2種算子組合，限制了其特征提取與噪聲抑制能力。實際軸承運行工況愈加復雜，導致原始振動信號中涵蓋大量噪聲信號，因此，需要進一步增強軸承故障特征的提取能力。

為了充分利用數學形態學針對非線性、非平穩過程的抗噪聲處理能力，避免多尺度形態學濾波權重系數配比不易尋優的缺點，有效發揮形態學算子乘積組合比平均組合更能突出故障信號周期性脈沖特征的優勢，提出了一種增強組合差分乘積形態學濾波（enhanced combination difference multiply morphological filter，ECDMMF）的軸承故障特征提取方法。在充分研究了4種基本形態學算子對正負脈沖提取性能的基礎上，通過對同類算子級聯、差分、乘積，進而構造一種新的組合差分乘積算子（combination difference multiply operation，CDMO），以獲取更多的脈沖信息，結合故障特征頻率比（characteristic frequency radio，CFR），優化乘積算子的SE參數，從而提取與SE相匹配的信號特征信息。在此基礎上，借助三階累積量切片譜技術（third-order cumulant slice spectrum，TOCSS）能夠有效抑制高斯噪聲、突出二次耦合成分的優點，提取軸承故障數據特征頻率及倍頻，進一步增強故障特征提取能力。

1增強組合差分乘積形態學濾波方法

1.1新形態算子構造

1.1.1 基本形態學算子定義及其特性分析

基本的形態學算子有4種：膨脹、腐蝕、閉合、打開。假定代表定義域為的一維離散信號函數，代表定義域為的結構元素離散函數，其中。基本算子膨脹（dilation）與腐蝕（erosion）定義如下：

軸承故障一維振動信號包含周期性沖擊脈沖特征，以上4種基本形態學算子都可以用于提取脈沖特征，但其表現出不同的脈沖特征提取性能^[11]，如表1所示。

由表1可知，利用腐蝕與打開運算可以提取軸承故障信號中的負沖擊特征，利用膨脹與閉合運算可以提取正沖擊特征；4種基本算子根據對沖擊特征的提取性能可分為2類：提取正沖擊的膨脹與閉合運算，提取負沖擊的腐蝕與打開運算。對同類形態算子進行級聯、組合能夠進一步提升其沖擊特征提取能力，同時保證特征提取的完整性。

1.1.2 組合差分乘積算子

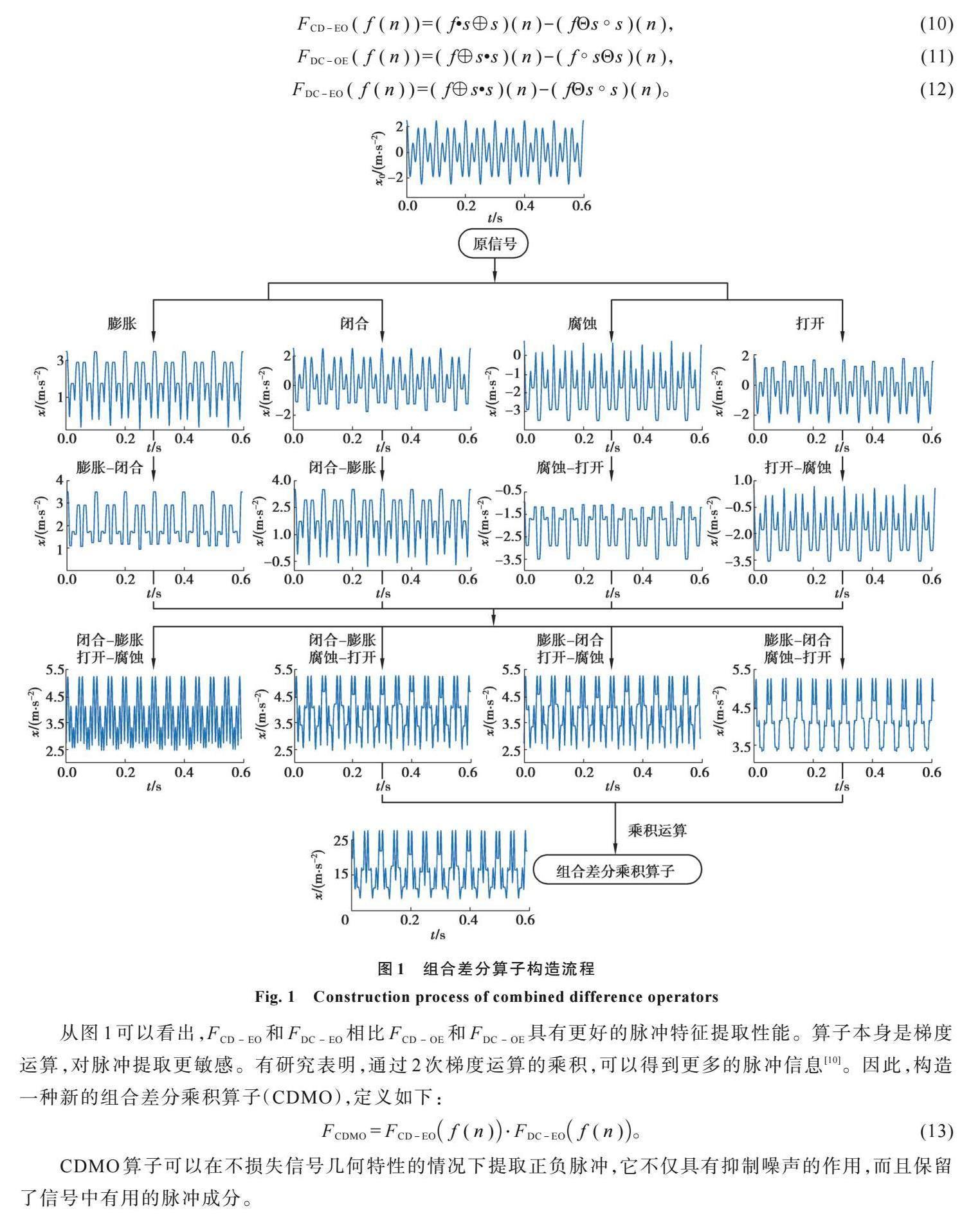
圖1是根據4種基本算子構造組合差分乘積算子的流程，利用仿真信號說明了該算子對脈沖提取效果的有效性，其中t為時間，x₀為輸入原信號。

從圖1可以看出，膨脹運算消除了負脈沖，使正脈沖更加平滑，腐蝕運算消除了正脈沖，使負脈沖更加平滑，而閉合運算保留了正脈沖，消除了負脈沖，打開運算消除了正脈沖，保留了負脈沖。

CDMO算子可以在不損失信號幾何特性的情況下提取正負脈沖，它不僅具有抑制噪聲的作用，而且保留了信號中有用的脈沖成分。

1.2三階累積量對角切片譜

高斯噪聲是軸承故障信號中最常見的噪聲之一，任何周期性和準周期性信號都可以被認為是非高斯信號，也可以被認為是滾動軸承自發產生的信號^[2]。因此，發生故障的軸承的振動信號基本上是非高斯信號，但因為運行環境的影響，還包含干擾信號分量，即高斯信號。高斯信號的高階譜為零，通過高階累積量變換可以去除，進而去除軸承振動信號中的噪聲干擾。

典型高階累積量變換技術——三階累積量切片譜可用于抑制高斯噪聲，同時具有抑制非二次相位耦合成分、計算量小的特點^[12]。通過該方法提取軸承故障數據特征頻率及其倍頻，能夠突出特征，增強故障特征提取能力，其基本原理如下。

1.3基于CFR指標的結構元素參數優化

在形態學濾波中，結構元素SE的設置對形態學濾波器的有效性有顯著的影響。SE參數由形狀、高度和長度3個要素決定，形狀對濾波效果的影響不大，為了減少計算量并提高計算效率，選擇與一維軸承振動信號形狀相似的零高度直線型結構元素，主要考慮SE長度對形態算子濾波性能的影響。

故障特征頻率比（CFR）是一種評價周期性脈沖提取效果的新指標，對軸承局部故障產生的特征信號比較敏感^[14]。因此，選取CFR作為衡量不同下，ECDMMF方法濾波性能的標準。CFR指標值定義如下：

1.4ECDMMF方法實現流程

增強組合差分乘積形態學濾波（ECDMMF）的軸承故障特征提取方法將新的形態學算子CDMO與TOCSS技術結合處理軸承故障原始信號。該方法實現流程如圖3所示。

根據流程圖，該方法實現步驟如下。

2實驗結果與分析

2.1軸承故障信號實驗

實際工程應用中信號運行環境更加復雜，所采集振動信號噪聲干擾更強，本研究中基于外圈故障（outer-race fault，OF）及內圈故障（inner-race fault，IF）信號實測數據驗證所提方法有效性。

2.2軸承外圈故障實驗

2.2.1 IMS軸承全壽命周期數據

利用辛辛那提大學智能維護系統（IMS）的軸承數據驗證本節方法^[16]。軸承故障實驗裝置如圖4所示。在全壽命周期數據采集過程中，每個軸承上通過2個PCB353B33加速度器記錄其轉動中的加速度，每10 min記錄1次，共984組數據。實驗完成后，發現軸承1出現了外圈故障。

實驗中所使用軸承的相關參數如表2所示。實驗載荷恒定為26.6 kN，電機轉速為2 000 r/min，采樣頻率為20 kHz。根據式（18）計算外圈故障特征頻率理論值可得=236.4 Hz。

2.2.2 ECDMMF方法實驗結果

根據2.2.1節介紹，選取IMS第541組數據進行分析，數據長度為8 192，提取其外圈故障的特征頻率。軸承早期故障原始信號的分析結果如圖6所示，包括時域波形、頻譜以及包絡譜，其中為幅值。

從圖6（b）頻譜圖中可以看出，外圈故障特征頻率很大程度上被噪聲分量掩蓋，無法提取236 Hz的頻率分量。圖6（c）的包絡譜中存在明顯的幾個頻率分量，但其均為轉頻33 Hz的倍頻，與外圈故障特征頻率無關；包絡譜中雖然可觀察到故障特征頻率分量，但與其他頻率分量幅值相比，其在包絡譜中并不突出。因此，僅依靠頻譜或者包絡譜無法提取由外圈故障導致的微弱脈沖特征，難以準確判斷軸承的故障類型。

利用ECDMMF方法處理IMS軸承故障信號，根據外圈故障特征頻率理論計算值以及采樣頻率，設定范圍為。各參數下ECDMMF方法濾波結果的CFR指標值如圖7（a）所示；在為3時，CFR指標最大，認為此時的濾波結果最佳，其TOCSS如圖7（b）所示。

從圖中可以看出4組幅值最突出的頻率分量為230 Hz及其倍頻。230 Hz與外圈故障特征頻率理論值236 Hz非常接近，誤差可能是由于一些濾波過程中的計算誤差引起，在可接受的范圍之內。ECDMMF方法分析處理IMS軸承故障信號后，抑制了噪聲干擾，準確提取出外圈故障的微弱脈沖，使其在其他頻率分量中具有較高的幅值。由此可以判斷該軸承的故障類型為外圈故障。

2.3軸承內圈故障實驗

2.3.1 XJTU-SY軸承全壽命周期數據

由于IMS軸承數據集僅有一種工況下的實驗，數據樣本比較單一，為了避免單一數據樣本無法全面驗證ECDMMF方法有效性的情況，采用西安交通大學的軸承全壽命周期數據（XJTU-SY）驗證ECDMMF方法的有效性。實驗所用的軸承加速壽命測試平臺（圖8）由交流電機、轉速控制器、轉軸等組成，通過液壓加載系統和轉速控制器調節徑向力和轉速，以實現不同工況的模擬。該實驗共設計了3種工況，每種工況下有5個軸承^[17]。

實驗中所用軸承為LDK UER滾動軸承，其相關參數如表3所示。選取徑向力為10 kN、電機轉速為2?400 r/min工況條件下第3個軸承的一段內圈故障信號進行研究，信號由水平方向加速度傳感器采集，采樣頻率為25.6 kHz。根據軸承相關參數由式（19）計算可得內圈故障特征頻率理論值=196.67 Hz。

所選取工況下的軸承共采集了371組樣本，每組樣本采樣時長為1.28 s，樣本間的采樣間隔為1 min。

類似IMS數據集中關于軸承全生命周期的劃分，計算371組樣本的，如圖9所示。選取最早出現波動的第341組數據研究，此時可能已經發生早期故障。

2.3.2 ECDMMF方法實驗結果

采用XJTU-SY軸承數據，選取第341組水平方向加速度信號進行分析，數據長度為8 192，圖10所示為原始數據時域波形、頻譜及包絡譜。從圖10（b）中能夠發現，頻率分量集中在1 000 Hz處，并且低頻段噪聲干擾多，無法從頻譜圖中提取。從圖10（c）中可以得到197 Hz的頻率分量，接近內圈故障頻率196.67 Hz，但其幅值非常小，并且在200 Hz前出現很多幅值較高的無法解釋來源的頻率分量。因此，僅通過頻譜或者包絡譜分析無法進行故障診斷。

利用ECDMMF方法處理XJTU-SY軸承故障原始信號，根據其采樣頻率以及內圈故障理論頻率值計算優化范圍為。各對應ECDMMF濾波結果的指標值如圖11（a）所示，最優形態學濾波結果的TOCSS如圖11（b）所示。

從圖中可以看出，L_SE=16時，CFR指標值最大，此時將獲得最優濾波結果。最優濾波結果的TOCSS所對應的0～600 Hz頻率區間內包含很多明顯的脈沖，其對應的數值都接近于轉頻=40 Hz以及內圈故障頻率=196.67 Hz的組合頻率。ECDMMF方法有效地提取了轉頻以及內圈故障頻率的一倍頻、二倍頻及三倍頻，并且濾波結果中包含的噪聲干擾分量非常少。由此可以判斷該軸承發生了內圈故障。

2.4對比分析

為了說明所提算法的有效性，將其與經典的WMMG方法^[8]以及近年來新提出的增強形態梯度乘積濾波（enhanced morphology gradient product filter， EMGPF）方法^[10]進行對比。

按照文獻[8]所述WMMG方法形態學算子以及多尺度加權方法，處理IMS外圈以及XJTU-SY內圈故障信號，其濾波結果如圖12所示。

從圖12（a）中可以得出，WMMG方法能夠準確提取轉頻及外圈故障信號的故障特征頻率，這2個頻率分量幅值最高。但是在分量附近仍然包含比較明顯的干擾分量脈沖，未提取出故障特征頻率的倍頻脈沖分量，且100 Hz以后并無有價值的脈沖分量，未體現軸承周期性沖擊性脈沖特征。從圖12（b）中可以得出，WMMG方法能夠提取轉頻及其二倍頻、內圈故障特征頻率，并且幅值最高。但是，內圈故障特征頻率倍頻的提取效果不佳，從頻譜中無法得出倍頻的脈沖分量。

相較于經典WMMG方法，本文所提ECDMMF方法不僅避免了多尺度加權方法的尋優問題，同時準確提取了軸承故障特征及其倍頻分量，最大程度抑制噪聲分量，為故障診斷提供了依據。

按照文獻[10]所述EMGPF方法實現細節處理IMS外圈以及XJTU-SY內圈故障信號，其濾波結果如圖13所示。

從圖13（a）可知，該方法能提取IMS信號的一倍頻、二倍頻及三倍頻，但其二倍頻及三倍頻脈沖幅值較低。ECDMMF方法不僅可以提取較突出及高幅值的二倍頻、三倍頻脈沖，而且可以提取四倍頻脈沖。相較于EMGPF方法，ECDMMF方法抑制噪聲的能力更好，尤其在頻段Hz處。

從圖13（b）可知，EMGPF方法同樣能提取XJTU-SY信號的以及的組合頻率分量，只有個別組合分量有差異。例如EMGPF未提取出的頻率分量，并且ECDMMF方法提取脈沖的幅值更高，尤其是在眾多有用分量中，內圈故障特征頻率分量及其倍頻更加突出。此外，ECDMMF濾波結果中噪聲干擾分量的毛刺更少，幅值更低，而EMGPF濾波結果在0～300 Hz處存在更多毛刺。

根據2種方法的原理，兩者的不同之處在于形態學算子的不同。可見，經過4種基本運算中同類算子級聯、差分組合之后比僅根據開閉算子組合具有更強的特征提取與抑制噪聲的能力。

3結束語

為確保準確提取軸承信號故障特征頻率，進一步增強故障特征提取能力，提出了ECDMMF方法。基于數值實驗并依托工程應用案例與經典的多尺度形態學濾波方法WMMG對比研究，結果表明ECDMMF方法能夠更加準確地提取軸承故障特征頻率及倍頻，所提取的與故障特征頻率相關的分量更完整，并且與噪聲干擾分量相比幅值更高，更易進行故障類別判斷。通過與EMGPF形態學濾波方法對比研究，表明新的組合差分乘積算子比僅根據2種形態運算構造的乘積算子的故障特征提取效果更好。

參考文獻

［1］??Li H， Liu T， Wu X， et al. Enhanced frequency band entropy method for fault feature extraction of rolling element bearings[J]. IEEE Transactions on Industrial Informatics， 2020， 16（9）： 5780-5791.

［2］??Li Y F， Liang X H， Zuo M J. Diagonal slice spectrum assisted optimal scale morphological filter for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing， 2017， 85： 146-161.

［3］??Lv C， Zhang P L， Wu D H， et al. Bearing fault signal analysis based on an adaptive multiscale combined morphological filter[J]. International Journal of Rotating Machinery， 2020， 2020（10）： 1-8.

［4］??何強， 唐向紅， 李傳江， 等. 負載不平衡下小樣本數據的軸承故障診斷[J]. 中國機械工程， 2021， 32（10）： 1164-1171， 1180.

He Q， Tang X H， Li C J， et al. Bearing fault diagnosis method based on small sample data under unbalanced loads[J]. China Mechanical Engineering， 2021， 32（10）： 1164-1171， 1180.（in Chinese）

［5］??范春旸， 吳守鵬， 劉曉文， 等. 基于小波包變換與隨機森林的滾動軸承故障特征分析方法[J]. 機械設計與制造， 2020（10）： 59-63， 70.

Fan C Y， Wu S P， Liu X W， et al. Fault feature analysis method of rolling bearing based on wavelet packet transform and random forest[J]. Machinery Design & Manufacture， 2020（10）： 59-63， 70.（in Chinese）

［6］??Gao S Z， Wang Q， Zhang Y M. Rolling bearing fault diagnosis based on CEEMDAN and refined composite multiscale fuzzy entropy[J]. IEEE Transactions on Instrumentation and Measurement， 2021， 70： 1-8.

［7］??Meng L J， Xiang J W， Wang Y X， et al. A hybrid fault diagnosis method using morphological filter-translation invariant wavelet and improved ensemble empirical mode decomposition[J]. Mechanical Systems and Signal Processing， 2015， 50/51： 101-115.

［8］??Li B， Zhang P L， Wang Z J， et al. A weighted multi-scale morphological gradient filter for rolling element bearing fault detection[J]. ISA Transactions， 2011， 50（4）： 599-608.

［9］??Lv J X， Yu J B. Average combination difference morphological filters for fault feature extraction of bearing[J]. Mechanical Systems and Signal Processing， 2018， 100： 827-845.

［10］??Li Y F， Zuo M J， Chen Y J， et al. An enhanced morphology gradient product filter for bearing fault detection[J]. Mechanical Systems and Signal Processing， 2018， 109： 166-184.

［11］??臧懷剛， 劉子豪， 李玉奎. 基于形態濾波和Laplace小波的軸承故障診斷[J]. 中國機械工程， 2016， 27（9）： 1198-1203.

Zang H G， Liu Z H， Li Y K. Fault diagnosis of bearings based on morphological filter and Laplace wavelet[J]. China Mechanical Engineering， 2016， 27（9）： 1198-1203.（in Chinese）

［12］??Jie B A， Huo C Q， Yu J J. Fault feature detection of rolling bearing based on LMD and third-order cumulant diagonal slice spectrum[J]. Applied Mechanics and Materials， 2016， 851： 333-339.

［13］??Nikias C L， Mendel J M. Signal processing with higher-order spectra[J]. IEEE Signal Processing Magazine， 1993， 10（3）： 10-37.

［14］??Wu D Y， Wang J W， Wang H， et al. An automatic bearing fault diagnosis method based on characteristics frequency ratio[J]. Sensors， 2020， 20（5）： 1519.

［15］??Dong Y B， Liao M F， Zhang X L， et al. Faults diagnosis of rolling element bearings based on modified morphological method[J]. Mechanical Systems and Signal Processing， 2011， 25（4）： 1276-1286.

［16］??The National Aeronautics and Space Administration. IMS data set [DS/OL]. [2021-08-07]. https：//ti.arc.nasa.gov/project/prognostic-data-repository.

［17］??雷亞國， 韓天宇， 王彪， 等. XJTU-SY滾動軸承加速壽命試驗數據集解讀[J]. 機械工程學報， 2019， 55（16）： 1-6.

Lei Y G， Han T Y， Wang B， et al. XJTU-SY rolling element bearing accelerated life test datasets： a tutorial[J]. Journal of Mechanical Engineering， 2019， 55（16）： 1-6.（in Chinese）

（編輯??呂建斌）