基于多模型自適應方法的智能汽車路徑跟蹤控制

梁藝瀟 李以農 Amir Khajepour 鄭玲 余穎弘 張紫微

收稿日期：2021-11-16

網絡出版日期：2022-04-13

基金項目：國家自然科學基金資助項目（51875061）。Foundation：Supported by National Natural Science Foundation of China （51875061）.

作者簡介：梁藝瀟（1993—），男，博士，主要研究方向為智能車輛規控技術，（E-mail） liangyixiao1119@foxmail.com。

通信作者：李以農，男，博士，教授，博士生導師，（E-mail）ynli@cqu.edu.cn。

摘要：路徑跟蹤控制是智能汽車的一項核心技術，跟蹤效果的精確性和在各種路面附著條件下的魯棒性是該技術的兩大關鍵要素。但汽車動力學模型的不確定性，尤其是輪胎側偏剛度的攝動使這兩者難以同時得到滿足。針對這一問題，將多模型自適應理論引入到智能汽車運動控制中處理不確定性系統的控制。首先，推導了多模型自適應控制律，提出了凸包構架下各個頂點的子模型對真實模型的自適應逼近律，并通過李雅普諾夫函數證明了所提出自適應律的收斂能力。在此基礎上建立了汽車動力學模型和車輛-路徑聯合模型，并由多個頂點子模型構建可覆蓋汽車輪胎側偏剛度攝動范圍的凸多面體，利用汽車動力學模型求解自適應率，通過車輛-路徑聯合模型，基于線性二次型方法（linear quadratic regulator， LQR）求解各個頂點的子模型處的反饋控制律，并通過所得出的自適應權重進行加權。基于Carsim/Simulink的聯合仿真結果表明，所提出的多模型自適應路徑跟蹤控制器在保證魯棒性的同時克服了傳統魯棒控制方法的保守性問題，與基于名義模型的LQR控制器和魯棒保性能控制器相比，在高附著路面和低附著路面上都可以取得更好的控制效果，很好地解決了路徑跟蹤控制中精確性與魯棒性之間的兩難問題。最后，通過快速原型測試平臺對算法進行了進一步的實驗驗證。結果表明，所提出的多模型自適應算法實時性良好，具有較好的工程應用潛力。

關鍵詞：智能汽車；車輛動力學；路徑跟蹤控制；模型不確定性；多模型自適應控制

中圖分類號：U27 ?????????文獻標志碼：A ???????????文章編號：1000-582X（2024）03-001-15

近年來，具有自動駕駛能力的智能汽車成了業界的研究熱點^[1-2]。路徑跟蹤控制是智能汽車的關鍵核心技術之一，旨在設計控制律使汽車完成對給定路徑的跟蹤。針對該問題，國內外學者展開了廣泛的研究，提出了包括比例-積分-微分（proportion， integral， and differential， PID）^[3]、模糊控制^[4]、滑模控制^[5]、最優控制^[6]和模型預測控制^[7-9]在內的多種路徑跟蹤算法。這些算法大致可分為2類：第1類的算法^[3-4]不需要建立參考模型，將汽車的動力學特征視為一個“黑箱”，其轉向控制的輸出僅僅取決于路徑跟蹤的偏差，這類算法往往需要大量的參數標定，且在理論上無法驗證控制器的可靠性；第2類算法^[5-9]需要建立汽車運動學/動力學模型，并基于控制理論對模型進行推導或迭代，以求解出可以使跟蹤偏差收斂的轉角控制量。第2類算法與第1類算法相比在可靠性上有顯著的提升，其中基于運動學模型的控制器，在中低車速和曲率較小的工況下可取得不錯的控制效果。但是，第2類算法由于忽略了汽車的側偏問題，不適用于車速較高以及會產生較大側向加速度的工況，相比之下，基于動力學模型的控制器在智能汽車路徑跟蹤控制中效果更佳^[5]。

然而，從系統動力學的角度來看，汽車是高度復雜的耦合的非線性系統，其動力學模型具有明顯的不確定性^[10]，對于智能汽車路徑跟蹤控制來說，輪胎側偏剛度的攝動是模型不確定性的主要來源，該值會隨路面附著系數、載荷、輪胎側偏角等參數的變化而變化^[11]。這類不確定性問題嚴重制約了智能汽車路徑跟蹤控制在不同工況下的魯棒性和精確性。為了解決這一問題，文獻^[12-16]中提出了魯棒控制的方案，通過不確定性參數的上下界對動力學模型進行擴維分析，設計控制器使智能汽車即使在輪胎側偏剛度偏離其標定名義值較多的惡劣工況下仍然能保證對跟蹤偏差的收斂能力。該類方法有效地提升了智能汽車路徑跟蹤控制的魯棒性，保證了智能汽車在低附著等條件下的控制性能。可是，由于魯棒控制方法往往基于最惡劣的條件展開研究，所設計的控制器為了保證魯棒性，在控制精確性上做了妥協，往往具有較強的保守性。在高速公路、城市道路等路面附著條件較好時，其控制精確性往往不如基于名義模型所設計的控制器。

考慮以上因素，筆者基于多模型自適應理論^[17]處理動力學模型不確定性系統的控制問題，解決路徑跟蹤控制中精確性與魯棒性之間難以權衡的難題，設計智能汽車的路徑跟蹤控制器，通過建立多個已知參數的汽車動力學頂點模型組成可包含各個工況條件下側偏剛度攝動的凸多面體，提出并證明具有偏差收斂能力的權值自適應律，建立車輛-路徑的聯合模型，在各個頂點處，基于線性二次型方法（linear quadratic regulator ，LQR）求解出反饋控制器，并進行相應的加權，實現多模型自適應的路徑跟蹤控制。由于凸多面體內任意一點都可以被各個頂點線性化地表示，所提出的控制器在保證魯棒性的同時也不受魯棒控制方法的保守性影響。Carsim-Simulink聯合仿真的結果驗證了本研究中提出方法的有效性和優越性。

1多模型自適應律推導

帶有不確定參數的多輸入多輸出（multiple-input multiple-output，MIMO）線性系統可表示為

式中：t為時間；λ為系統中具有不確定性的參數；A_p（λ）和B_p（λ）是帶有不確定性的狀態空間方程矩陣，其不確定性取決于參數；x_p（t）和u（t）分別代表系統的狀態量和輸入，二者都是可測的。

對于式（1）所述的系統，若存在N個已知的系統矩陣組合A_i和B_i（i=1，2，…，N），在N的數值、A_i和B_i的取值滿足一定條件的基礎上，對于任意可能的參數λ，不確定性矩陣可表示為^[17]

式中，Co{·}代表一組矩陣集合的凸包，在幾何上也可將其表示為一個凸多面體。

對于凸包中的每一個頂點i∈{1，2，…，N}，其定參數動力學模型為

那么，由式（2）表示的矩陣集合的凸包含性質可以導出相應的自適應律。根據式（3），式（2）可被重新表示為

式中，w_i（t）表示在t時刻每個頂點處子模型的權值，應滿足以下條件：

式（5）中對于任意給定的λ，w_i的值在線性時不變（linear time-invariant，LTI）系統中也是恒定的。

由于頂點處子模型的參數矩陣A_i和B_i是已知的，對未知的不確定性矩陣A_p（λ）和B_p（λ）的辨識可以等價于對未知權值w_i的估計，這樣就實現了問題的轉化。針對系統的在線辨識問題，引入線性參數模型將式（2）寫為^[18]

式中：s表示微分算子；γ是恒定的正數；為推導計算中的算子。式（4）中的N個恒定頂點參數矩陣也可以類似地參數化：

式中。那么，各個頂點處子模型的估計偏差為

由式（4）和（5）可得

式（9）可用下面的矩陣表示：

基于式（5）和式（10）得到頂點處子模型中的最后一項，即第N項的權重為。因此，通過在式（10）的兩端同時減去第N項模型的偏差ε_N（t），得到如下關系式：

該式的導出為凸面體的權重辨識自適應律奠定了基礎。將式（11）第一項中等式右端的項移到左端，并與E_R（t）的轉置相乘，可得

基于梯度下降法^[17]，設計如下權重估計的自適應律：

式中，Γ是用于調整收斂速率的對稱正定矩陣。

此處，假設各個頂點的實際權重為，那么估計誤差可表示為。將其代入式（11）中的第一項，可得

為了證明所提出的自適應律的收斂能力，定義李雅普諾夫函數

結合式（13）和式（14）得如下關系式：

對式（15）中的李雅普諾夫函數求導，并代入式（16）得

由此，自適應律（13）的收斂能力得到了證明。

需要注意的是，雖然該自適應律可以使偏差收斂，并滿足式（5）中的第一項條件，但其并不能保證滿足式（5）中的第二項條件，即w_i（t）≥0，i=1，2，…，N。為了保證滿足該條件，在自適應律中引入梯度投影法。首先，將式（5）中的約束表示為

為了使式（18）具有式（5）的約束能力，函數g定義為

式中。

將S⁰和?S分別定義為S集的內部和邊界，應用梯度投影法后，自適應律（13）可通過以下算法表示：

2智能汽車路徑跟蹤多模型自適應控制

2.1模型建立

在控制器的設計中，采用圖1所示的二自由度簡化車輛單軌動力學模型，該模型忽略了側傾、俯仰、垂向運動和懸架的作用，在車輛動力學與控制領域中得到了廣泛應用。其狀態空間方程為^[15]

式中：狀態量，這里的v_y和r分別是汽車的側向速度和橫擺角速度；輸入，這里的δ_f為前輪轉角；狀態空間矩陣

式中：v_x是汽車的縱向速度；m和I_z分別是汽車的質量和繞質心處垂向軸的轉動慣量；l_f和l_r分別是汽車質心到前軸和后軸的距離；c_f和c_r分別表示前輪和后輪的側偏剛度，其數值隨路面附著系數、載荷、輪胎側偏角等參數的變化而攝動，在一些較為極限的工況下，其真實值與名義值之間有極大的差異。對于汽車橫向控制來說，側偏剛度的攝動是模型不確定性的最顯著體現。圖1中X和Y是大地坐標系的坐標軸，F_yf和F_yr分別為前輪和后輪的側偏力，α_f和α_r分別為前輪和后輪的側偏角。

車輛實際位置與參考路徑之間的相對關系如圖2所示，圖中e_y是汽車的質心與參考路徑上最近點d之間的橫向偏差，S是沿參考路徑的弧長，Ψ_d和Ψ分別是參考路徑上的期望航向角與汽車的實際航向角，因而汽車的航向角偏差定義為ΔΨ=Ψ-Ψ_d。基于Serret-Frenet坐標系，通過小角度假設進行線性化，可得

將式（22）與式（23）結合得到由狀態空間表示的車輛-路徑聯合模型的動力學方程（24），其中，狀態量x_c=[e_yΔψv_yr]^T，控制輸入量，擾動為k=[0v_xρ 0 0]^T。此外，基于狀態量都可以準確測量/估計的假設，控制器將采用全狀態反饋的方案。

2.2自適應控制律

采用了如圖3所示的4組側偏剛度（c_f1，c_r1） （c_f2，c_r2） （c_f3，c_r3） （c_f4，c_r4）作為多模型自適應中頂點模型的側偏剛度，取值自Carsim中的魔術輪胎模型，（c_fn，c_rn）代表前后軸側偏剛度的真實值。其中，（c_f1，c_r1）和（c_f2，c_r2）分別是在附著系數為1時的高附著路面下和輪胎側偏角僅為0.5°時的側偏剛度，其取值的差異是由于選擇了不同的前后軸垂向載荷分布（汽車加/減速會影響前后軸的垂向載荷，進而影響前后軸輪胎側偏剛度）；（c_f3，c_r3）和（c_f4，c_r4）則分別為汽車在附著系數為0.2的低附著路面下和有較大輪胎側偏角時的側偏剛度。可以看出，這4組側偏剛度組成的區域（圖3中的陰影部分）可涵蓋汽車在不同負載和不同路面附著等條件下的絕大多數情形，且區域內任何一個點都可以用4個頂點線性表示，由此實現了對不確定模型的凸包含。

整體的控制架構如圖4所示。基于式（22）中的動力學模型來求解各個頂點的實時自適應權重，并以此對各個頂點對應車輛-路徑聯合模型（24）求得的狀態反饋控制增益進行加權，實現多模型的自適應控制。

對各個頂點的車輛-路徑聯合模型，基于LQR方法設計控制器，使循跡偏差最小化，以保證汽車的動力學穩定性，其性能泛函為

式中：Q是半正定的狀態量權重矩陣；R是正定的輸入量權重。

相應地，最優反饋控制量表示為

式中：K_i為所計算的反饋增益；P_i是式（27）中Riccati方程的正定解。

因此，智能汽車多模型自適應路徑跟蹤控制的輸入為

3仿真與分析

采用Simulink-CarSim聯合仿真的方法對所提控制算法的效果進行驗證。在Simulink中搭建控制算法，選取Carsim中的E型轎車作為仿真模型，其模型參數如表1所示。

選擇常見的雙移線工況對所提出控制算法進行驗證，其曲率如圖5所示。

在仿真中，汽車以60 km/h的速度分別在路面附著系數為0.85的高附著路面和路面附著系數為0.35的低附著路面完成雙移線操作。為了更好地描述控制器的效果，引入了其他2組控制器進行對比：對比控制器1基于名義模型，采用LQR方法設計控制器，在仿真圖表中簡稱為LQR；對比控制器2引入了文獻[13]中采用的魯棒保性能（robust-guaranteed-cost，RGC）控制器，該控制器在最優控制器架構的基礎上，基于線性矩陣不等式方法（linear-matrix-inequality，LMI）對輪胎側偏剛度攝動的上下界進行擴維，由此求解出最優的反饋增益，在圖表中簡寫為RGC。本研究中所設計的多模型自適應控制器簡寫為MMAC。為了實現更客觀的對比，對3組控制器采用了同樣的權重矩陣Q和R。此外，仿真中的多模型自適應控制所采用的4個頂點模型的前后軸輪胎剛度分別為：（140?000，110 000） （110 000，140 000） （30 000，20 000） （20 000，30?000），單位為N/rad。

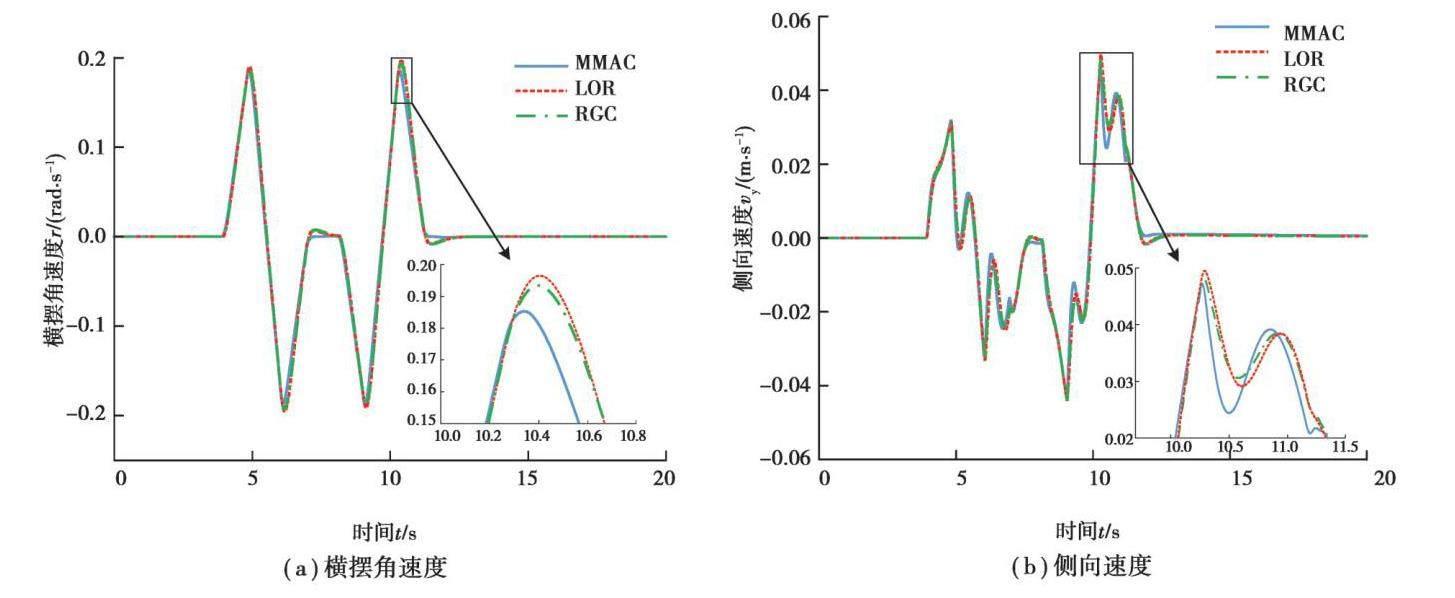
在第1組仿真中，智能汽車在高附著路面（μ=0.85）以60 km/h的速度完成對給定雙移線路徑的跟蹤，其路徑跟蹤情況如圖6所示。從圖6（a）中可以看出，雖然3組控制器在高附著路面下都能完成較精確的路徑跟蹤，但MMAC的偏差明顯小于其他2種方法，這也說明即使在高附著路面上，基于理想狀況標定出的名義側偏剛度仍然和汽車面臨的實際情況有一定差異。基于名義模型的LQR控制器的跟蹤效果略好于魯棒保性能控制器，這也反映了上文中所提到的魯棒控制器在正常工況下的保守性，同樣的現象也可以從圖6（b）中的航向角偏差看出。圖6（c）中的全局路徑顯示，3組控制器都可以很好地完成對給定雙移線路徑的跟蹤，但多模型自適應控制器的完成質量明顯好于2組對比控制器。

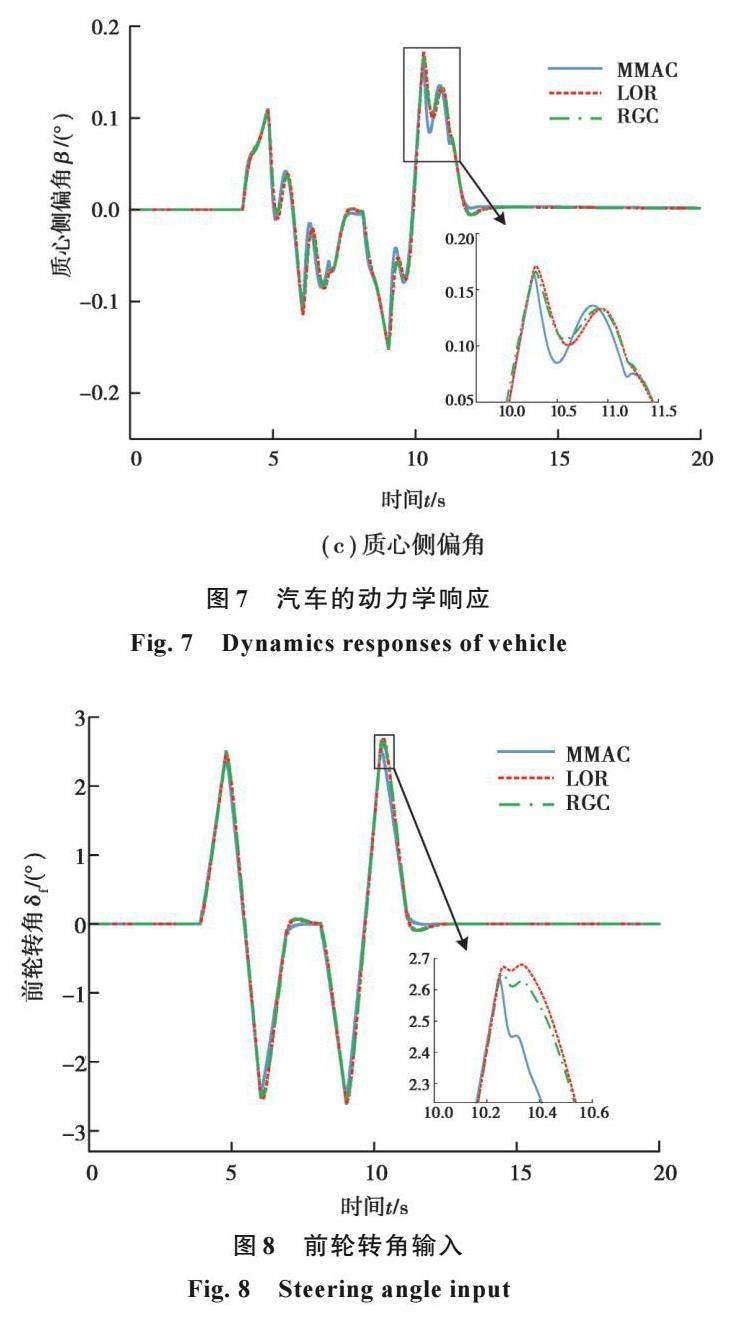
在此工況下，仿真計算得到汽車的動力學響應如圖7所示。可以看出，3種控制器的動力學響應基本一致。但是MMAC的側向速度和質心側偏角的峰值仍然略小于另2組控制器，這也反映了其在保證汽車的動力學穩定性和可控性上有更強的能力。圖8是汽車的前輪轉角，從中可知，3組控制器輸出的控制量都在合理的范圍內。

3.2低附著路面仿真

為了進一步驗證所提出的方法，第2組仿真實驗中，將路面附著系數調整為0.35，該類附著系數常見于雨雪后的濕滑路面，在這類路面上，輪胎側偏剛度往往相對其名義值有較大的偏差。在該路面條件下，智能汽車仍以60 km/h的時速完成上述的雙移線路徑跟蹤，以測試控制器的魯棒性。圖9為汽車的路徑跟蹤情況，從中可以看出，所提出的控制器在低附著工況下仍然具有最好的跟蹤的性能，而此時基于名義模型的LQR控制器的性能已明顯不如魯棒保性能控制器。而且，從圖9（b）中可以發現，基于名義模型LQR控制器的航向角偏差在完成雙移線第2個換道時出現了嚴重的超調，這從圖9（c）的全局路徑中也能看出，相比于多模型自適應控制器和魯棒保性能控制器，該控制器在經過反復調整后，才消除了變換回原車道后的超調偏差。這些結果表明，在低附著工況下，基于名義模型的控制器開始出現明顯的不足，而魯棒控制和本文中提出的多模型自適應控制方法仍然可以保證較好的控制效果。

對低附著路面工況，仿真計算得到汽車的動力學響應如圖10所示。可以發現，多模型自適應控制器和魯棒保性能控制器在低附著路面上仍然可以較好地保證汽車的動力學性能，而基于名義模型的LQR控制器的動力學響應出現了明顯的異常，其各參數在第2次換道時均出現明顯的超調和振蕩，這對汽車的動力學穩定性十分不利。相似的情況也出現在圖11的前輪轉角輸入中，基于名義模型的LQR控制器的輸入在第2次換道一開始就出現了異常的情況，而多模型自適應控制器和魯棒控制器的輸入響應都在合理的范圍內，這也進一步驗證了所提出方法的優越性。

3.3定量分析

為了更加深入地分析仿真結果，計算了汽車的路徑跟蹤橫向偏差和航向角偏差的均方根值和最大值（表2）以及汽車質心側偏角的均方根值和最大值（表3）來定量分析控制器的路徑跟蹤性能和汽車的動力學穩定性，在高附著和低附著路面下的均方根值的相對比值越高，說明控制器的性能保持能力越強。對表中的數據進行定量分析可以看出，基于名義模型的LQR控制器在低附著路面上的性能與高附著路面相比明顯下降，而魯棒保性能控制器（RGC）在低附著路面上的性能與高附著路面比較接近，這也體現了魯棒控制方法的特點。本研究中提出的多模型自適應控制器（MMAPC），雖然在路面附著變化下的性能保持能力不如魯棒控制方法，但由于其相比于魯棒控制方法較低的保守性，在高附著和低附著路面上都取得了最佳的控制效果。

3.4快速原型驗證

前面的對比研究分析證明了所提出多模型自適應算法在智能汽車運動控制中的優越性。但是，由于仿真分析的目的是通過對比研究對普通控制方法、魯棒控制方法及所提出的多模型自適應控制方法在不同路面條件下的特征進行分析，因此所使用的車速不高。為了更加充分地驗證所提出的多模型自適應控制器的適用性，本節將在更高的速度下對其進行測試。

實車試驗在汽車動力學與控制的相關研究中具有最強的說服力，但是由于中高速工況下智能汽車運動控制和輔助駕駛控制的實車驗證較危險及開展試驗的相關條件不夠成熟，目前對于相關控制策略的實車驗證集中在低速工況（0～40 km/h）^[19-20]。基于對安全性及設備條件的考慮，已報道的相關研究主要選擇硬件在環或快速原型試驗臺對算法進行初步試驗驗證^[21-22]。因此，為更好地驗證所提出算法，選擇了快速原型測試的方案對控制算法進行實物在環測試，并對其實時性進行驗證。在所設計的方案中，仿真驗證的車輛模型仍然使用Carsim中的動力學模型，并在設計控制器的Simulink中加入實時內核。試驗測試時，控制信號通過CAN卡和轉換器傳給電機驅動，進而對轉向電機進行實時控制。圖12為根據所采用的快速原型測試方案搭建的平臺，該平臺由計算機、CAN卡、轉換器、電機驅動、轉向電機和顯示界面等組成。

快速原型測試中仍然使用對比分析中采用的雙移線路徑。設定車速為90 km/h，路面附著系數μ=0.65，該值處于對比研究分析中的高附著條件和低附著條件之間，屬于中等附著的路面條件。測試結果如圖13所示。

多模型控制算法在速度較高的工況下仍能準確地跟蹤參考路徑（圖13（a）～（c）），其橫向偏差和航向角偏差的最大值分別僅為0.133 3 m和2.690 7°。車輛的橫擺角速度變化平穩，并且其側向速度和質心側偏角都在合理的范圍內（圖13（d）～（f）），這表明在整個運動過程中，車輛的操縱性和穩定性保持良好。控制器計算出的參考值和CAN卡傳遞的轉向信號（圖13（g））能夠精確同步。算法的單步求解耗時基本維持在0.001～0.004?s之間（圖13（h）），遠小于所設置的采樣時間0.01 s，證明了所提出自適應算法求解的實時性。對比研究分析和快速原型試驗都表明所提出的多模型自適應算法在智能汽車運動控制中能夠很好地處理當前各種控制算法在精確性與魯棒性之間的兩難問題。

為進一步論述所提出的控制器在高速工況下的性能，在快速原型驗證的工況條件下對MMAC、LQR和RGC這3組控制器進行對比分析（圖14）。需要說明的是，由于本研究中所選擇的雙移線路徑曲率較大，在速度較高時，若附著較低，很容易超越汽車的物理附著極限。快速原型驗證中選擇的工況已經接近物理附著極限，故該工況可以充分證明所提出的方法在高速下的性能。可以看出在高速工況下，3組控制器都能夠完成軌跡跟蹤的控制目標，而MMAC控制的效果明顯好于LQR和RGC。值得一提的是，LQR控制和RGC控制都是比較有代表性的控制算法，在自動駕駛汽車軌跡跟蹤控制的研究中已經有了很多應用，其有效性已經得到了廣泛的認同，通過與這二者進行對比，多模型自適應算法MMAC的有效性和優越性都得到了充分證明。

4結??論

1） 針對智能汽車路徑跟蹤控制中輪胎側偏剛度攝動導致的模型不確定性問題，提出了一種不同于傳統魯棒控制方法的多模型自適應控制方法。

2） 研究證明，所提出的多模型自適應路徑跟蹤控制器在不同路面附著條件下都能保證良好的性能。在高附著路面上可以實現最精確的路徑跟蹤控制，而在低附著路面上對模型不確定性的控制問題也具有良好的魯棒性。

3） 在對比研究分析的基礎上進行了快速原型試驗，進一步驗證了多模型自適應算法的有效性和適用性。結果顯示多模型自適應算法可以很好地保證實時性，具有良好的工程應用潛力。

4） 多模型自適應控制方法在保證魯棒性的同時克服了傳統的魯棒控制方法保守性較強的問題，無需在控制性能與魯棒性能之間進行妥協，為不確定性系統的控制器設計引入了新的思路。

后續的研究將在自適應算法中把車輛信號的噪聲考慮進來，研究在信號噪聲的干擾下如何保證控制器的精確性和魯棒性。

參考文獻

［1］??《中國公路學報》編輯部. 中國汽車工程學術研究綜述·2017[J]. 中國公路學報， 2017， 30（6）： 1-197.

Editorial Department of China Journal of Highway and Transport. Review on Chinas automotive engineering research progress： 2017[J]. China Journal of Highway and Transport， 2017， 30（6）： 1-197. （in Chinese）

［2］??Levinson J， Askeland J， Becker J， et al. Towards fully autonomous driving： systems and algorithms[C]//2011 IEEE Intelligent Vehicles Symposium （IV）， June 5-9， 2011， Baden-Baden， Germany. IEEE， 2011： 163-168.

［3］??Marino R， Scalzi S， Netto M. Nested PID steering control for lane keeping in autonomous vehicles[J]. Control Engineering Practice， 2011， 19（12）： 1459-1467.

［4］??汪偉， 趙又群， 許健雄， 等. 基于模糊控制的汽車路徑跟蹤研究[J]. 中國機械工程， 2014， 25（18）： 2532-2538.

Wang W， Zhao Y Q， Xu J X， et al. Research on vehicle path tracking based on fuzzy control[J]. China Mechanical Engineering， 2014， 25（18）： 2532-2538. （in Chinese）

［5］??Hu C， Qin Y C， Cao H T， et al. Lane keeping of autonomous vehicles based on differential steering with adaptive multivariable super-twisting control[J]. Mechanical Systems and Signal Processing， 2019， 125： 330-346.

［6］??郭應時， 蔣拯民， 白艷， 等. 無人駕駛汽車路徑跟蹤控制方法擬人程度研究[J]. 中國公路學報， 2018， 31（8）： 189-196.

Guo Y S， Jiang Z M， Bai Y， et al. Investigation of humanoid level of path tracking methods based on autonomous vehicles[J]. China Journal of Highway and Transport， 2018， 31（8）： 189-196. （in Chinese）

［7］??汪選要， 程義， 程煜， 等. 低附著系數路面車道保持模型預測控制及汽車穩定性控制[J]. 中國機械工程， 2019， 30（9）： 1018-1025.

Wang X Y， Cheng Y， Cheng Y， et al. Lane keeping model prediction control and vehicle stability control on low adhesion coefficient roads[J]. China Mechanical Engineering， 2019， 30（9）： 1018-1025. （in Chinese）

［8］??Ji J， Khajepour A， Melek W W， et al. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints[J]. IEEE Transactions on Vehicular Technology， 2017， 66（2）： 952-964.

［9］??李軍， 唐爽， 黃志祥， 等. 融合穩定性的高速無人駕駛車輛縱橫向協調控制方法[J]. 交通運輸工程學報， 2020， 20（2）： 205-218.

Li J， Tang S， Huang Z X， et al. A coordinated control method for high speed unmanned vehicle with integrated stability[J]. Journal of Traffic and Transportation Engineering， 2020， 20（2）： 205-218. （in Chinese）

［10］??李亮， 賈鋼， 宋健， 等. 汽車動力學穩定性控制研究進展[J]. 機械工程學報， 2013， 49（24）： 95-107.

Li L， Jia G， Song J， et al. Progress on vehicle dynamics stability control system[J]. Journal of Mechanical Engineering， 2013， 49（24）： 95-107. （in Chinese）

［11］??黃彩霞， 雷飛， 胡林， 等. 輪轂電機驅動汽車區域極點配置橫向穩定性控制[J]. 汽車工程， 2019， 41（8）： 905-914.

Huang C X， Lei F， Hu L， et al. Lateral stability control based on regional pole placement of in-wheel-motored electric vehicle[J]. Automotive Engineering， 2019， 41（8）： 905-914. （in Chinese）

［12］??Wang J X， Dai M M， Yin G D， et al. Output-feedback robust control for vehicle path tracking considering different human drivers?characteristics[J]. Mechatronics， 2018， 50： 402-412.

［13］??Guo J H， Luo Y G， Li K Q. Robust gain-scheduling automatic steering control of unmanned ground vehicles under velocity-varying motion[J]. Vehicle System Dynamics， 2019， 57（4）： 595-616.

［14］??Wang R R， Jing H， Hu C， et al. RobustH_∞path following control for autonomous ground vehicles with delay and data dropout[J]. IEEE Transactions on Intelligent Transportation Systems， 2016， 17（7）： 2042-2050.

［15］??Guo J H， Wang J， Hu P， et al. Robust guaranteed-cost path-following control for autonomous vehicles on unstructured roads[J]. Proceedings of the Institution of Mechanical Engineers， Part D： Journal of Automobile Engineering， 2018， 232（7）： 896-908.

［16］??劉瑞， 朱西產， 李霖. 緊急變道工況魯棒性車輛軌跡跟蹤策略[J]. 同濟大學學報（自然科學版）， 2017， 45（11）： 1659-1663.

Liu R， Zhu X C， Li L. Robust trajectory following strategy during emergency lane-change condition[J]. Journal of Tongji University （Natural Science）， 2017， 45（11）： 1659-1663. （in Chinese）

［17］??Zengin H， Zengin N， Fidan B， et al. Blending based multiple-model adaptive control of multivariable systems with application to lateral vehicle motion control[J]. European Journal of Control， 2021， 58： 1-10.

［18］??Lemos J M， Neves-Silva R， Igreja J M. Solar energy collector systems[M]//Adaptive control of solar energy collector systems. Cham： Springer International Publishing， 2014： 1-25.

［19］??蔡英鳳， 臧勇， 孫曉強， 等. 基于可拓切換控制方法的智能車輛車道保持系統研究[J]. 中國公路學報， 2019， 32（6）： 43-52.

Cai Y F， Zang Y， Sun X Q， et al. Research on intelligent vehicle lane keeping system based on extension switch control method[J]. China Journal of Highway and Transport， 2019， 32（6）： 43-52. （in Chinese）

［20］??張炳力， 李子龍， 沈干， 等. 基于模糊神經網絡的智能汽車軌跡跟蹤研究[J]. 汽車工程， 2019， 41（8）： 953-959.

Zhang B L， Li Z L， Shen G， et al. A research on path tracking of intelligent vehicle based on fuzzy neural network[J]. Automotive Engineering， 2019， 41（8）： 953-959. （in Chinese）

［21］??Cheng S， Li L， Mei M M， et al. Multiple-objective adaptive cruise control system integrated with DYC[J]. IEEE Transactions on Vehicular Technology， 2019， 68（5）： 4550-4559.

［22］??Zhang B H， Lu S B. Fault-tolerant control for four-wheel independent actuated electric vehicle using feedback linearization and cooperative game theory[J]. Control Engineering Practice， 2020， 101： 104510.

（編輯??羅敏）