基于改進粒子濾波算法的車速估計

高彥 傅春耘 楊忠 楊官龍

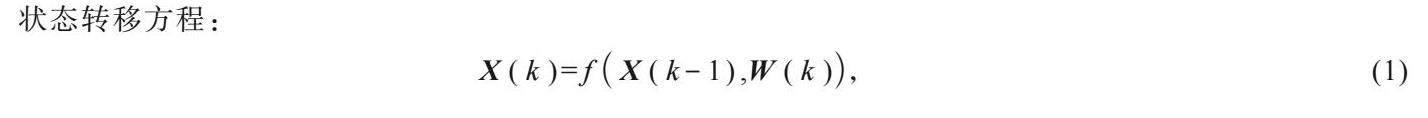
收稿日期：2021-12-27

網絡出版日期：2022-04-24

基金項目：重慶市自然科學基金資助項目（cstc2020jcyj-msxmX0664）；中央高校基本科研業務費項目（2020CDJ-LHZZ-043）。

作者簡介：高彥（1994—），男，碩士研究生，主要從事智能汽車底盤控制研究，（E-mail）gaoyan_cqu@cqu.edu.cn。

通信作者：傅春耘，男，副教授，（E-mail）fuchunyun@cqu.edu.cn。

摘要：針對基于粒子濾波算法設計的車速估計器因提議分布與實際分布不一致導致粒子退化使估計誤差變大的問題，提出了一種通過修正提議分布減弱粒子退化影響的改進粒子濾波車速估計器。首先，基于車輛運動學模型和傳感器特性建立系統的狀態轉移方程和觀測方程。然后，利用傳感器測量值與粒子狀態值的差值設計提議分布修正項對狀態轉移方程進行修正，并對過程噪聲做自適應處理。最后，利用CarSim-Simulink聯合仿真平臺在雙移線工況和正弦轉角輸入工況下進行仿真驗證。與自適應粒子濾波器相比，雙移線工況下改進粒子濾波估計器產生的縱向速度估計值和側向速度估計值的平均絕對誤差分別減小了40.25%和55.71%；正弦轉角輸入工況下，改進粒子濾波估計器產生的縱向速度估計值和側向速度估計值的平均絕對誤差分別減小了47.00%和41.21%。

關鍵詞：車速估計；粒子濾波；提議分布

中圖分類號：U461 ?????????文獻標志碼：A ????????????文章編號：1000-582X（2024）03-044-09

隨著現代汽車電子控制技術的快速發展，車載控制系統的數量越來越多。許多控制系統在工作時需要車輛的狀態信息作為控制系統的輸入，例如自適應巡航控制（adaptive cruise control，ACC）、電子穩定控制（electronic stability control，ESC）、防抱死制動系統（anti-lock braking system，ABS）。因此，獲取準確的車輛狀態信息是車輛控制系統正常、有效工作的前提^[1]。車輛狀態信息中存在的誤差將使車輛控制系統的性能下降甚至完全喪失。

在車輛的諸多狀態中，車速（包括縱向速度和側向速度）是最重要的車輛狀態之一，許多重要的車載控制系統均需要準確的車速信息才能正常工作。由于通過傳感器直接獲取準確車速的成本很高，因此目前車速信息主要通過狀態估計來間接獲取。常用的狀態估計方法包括卡爾曼濾波算法、龍貝格觀測器、魯棒觀測器、滑模觀測器和非線性觀測器等，其中卡爾曼濾波算法是應用最廣泛的狀態估計算法^[2]。卡爾曼濾波算法又衍生出多種變體，例如擴展卡爾曼濾波（extended Kalman filter，EKF）、無跡卡爾曼濾波（unscented Kalman filter，UKF）、容積卡爾曼濾波（cubature Kalman filter，CKF）等。文獻[3-5]中采用經典卡爾曼濾波算法估計車速，該方法以線性微分方程為基礎，所以只適用于線性系統。但是，車輛的運行工況復雜多變，當車輛運行在極限工況下時，車輛系統表現出強非線性。因此，文獻[6-9]中使用擴展卡爾曼濾波算法進行車速估計，但是該方法只適用于弱非線性系統，而且需要計算復雜的雅可比矩陣。文獻[1，10-12]中采用無跡卡爾曼濾波算法估計車速，該方法不需要計算雅可比矩陣，能處理不可導的非線性函數，與擴展卡爾曼濾波算法相比更適用于非線性系統。文獻[13-14]中采用容積卡爾曼濾波算法估計車速，該方法不需要計算復雜的雅可比矩陣，且計算多維函數積分時效率較高，在非線性濾波方面較其他種類的卡爾曼濾波器具有更大的優勢^[15]。

上述各種基于卡爾曼濾波的車速估計算法都在處理強非線性系統方面存在缺陷。粒子濾波算法最早出現在20世紀50年代，是一種基于蒙特卡洛法和遞歸貝葉斯估計的統計濾波方法，具有很強的非線性處理能力^[16]。文獻[16-19]中采用粒子濾波算法來估計車速，結果表明文獻中的幾種粒子濾波估計器均能夠在強非線性工況下較準確地估計車速。

雖然上述粒子濾波算法具有很強的非線性處理能力，并且通過重采樣方法在一定程度上減弱了粒子退化對估計精度的影響，但是仍然存在粒子退化導致估計精度變差的問題。具體來講，隨著粒子濾波算法迭代次數增加，只有少部分粒子具有較大的權重，大部分粒子的權重很小，造成粒子多樣性匱乏，從而影響估計精度^[20]。針對這一問題，文獻[17]中采用高斯分布作為提議分布，設計了自適應標準差參數，在每一個采樣時刻修正提議分布的標準差，提升了粒子濾波估計器的估計精度和適應能力。但是該方法仍然存在因提議分布與實際分布不一致導致的粒子退化問題。筆者在文獻[17]的基礎上基于車輛運動學模型設計了一種改進粒子濾波估計器，改進提議分布使其更符合實際分布以進一步減弱粒子退化對估計精度的影響，從而有效估計車輛的縱向速度和側向速度。仿真結果表明，與文獻[17]中的自適應粒子濾波估計器相比，改進粒子濾波估計器在雙移線和正弦轉角輸入工況下均使縱向速度和側向速度估計值的平均絕對誤差大幅減小。

1粒子濾波算法基本原理

粒子濾波適用于強非線性系統，因此非常適用于處理車輛狀態估計問題^[21]。粒子濾波的核心思想是用一系列離散隨機采樣點來近似系統隨機變量的概率密度，以樣本均值代替積分運算，從而獲得狀態的最小方差估計^[22]。

與卡爾曼濾波一樣，粒子濾波算法利用狀態空間模型對系統進行描述，該模型包括狀態轉移方程和觀測方程。

式中：表示系統時刻的狀態；表示系統時刻的狀態；表示系統時刻的過程噪聲；表示傳感器時刻的測量結果；表示傳感器時刻的測量噪聲；f為狀態轉移函數；h為觀測函數。

粒子濾波的均值思想是利用粒子集合的均值作為狀態的估計值。如果粒子集合的分布不能很好地“覆蓋”真實值，粒子濾波器就會出現濾波發散現象。粒子集合的有效性通過粒子的權重計算和粒子集合的重采樣2個步驟來保證。粒子濾波算法中粒子集合的迭代過程如下^[23]。

1）將表示系統時刻狀態的每一個粒子代入式（1），得到系統狀態的一步預測值。其中表示第個粒子，表示粒子集合的粒子數。

2）將一步預測狀態集合中的每一個粒子帶入式（2），計算觀測值的預測值。

3）假設在當前時刻（即時刻），傳感器采集到唯一的觀測值，則可以根據該觀測值來計算每個粒子的權重：

式中：表示觀測值的預測值與當前時刻觀測值的差值；g為粒子的權重計算函數；表示粒子的權重。需要指出的是g必須體現“觀測值的預測值與傳感器真實觀測值的絕對偏差越小，權重越大，反之權重越小”這一規律。高斯函數是其中一種比較具有代表性的權重計算函數。

4）對粒子集合進行重采樣。重采樣過程體現的是粒子濾波過程中的“優勝劣汰”，即：復制權重大的粒子，淘汰權重小的粒子，并保證重采樣前后的粒子數量一致。重采樣原理如圖1所示。通過重采樣機制，可在一定程度抑制粒子退化，保證粒子濾波的狀態估計效果。

5）將重采樣后的粒子集合表示的狀態記為，代入到下一個迭代循環中。

2基于改進粒子濾波的車速估計

2.1車輛運動學模型

車輛的運動學模型如圖2所示。在汽車運動過程中，如下運動學關系始終成立：

式中：和分別表示汽車的縱向和側向速度；和分別表示汽車的縱向和側向加速度；表示汽車的橫擺角速度。

2.2狀態轉移方程和觀測方程

根據式（5）和式（6）得到汽車縱向速度、側向速度的離散表達式如下：

2.3提議分布修正項

粒子濾波算法效果的好壞取決于粒子集合能否準確地“覆蓋”真實值，如果不能很好地“覆蓋”真實值則會出現粒子退化問題，從而導致粒子濾波算法的狀態估計效果變差。為了減小粒子退化的影響，通常采取以下3種措施^[25]：

1）增加粒子數；

2）采用能更有效抑制粒子退化的重采樣技術；

3）選擇合理的生成粒子的提議分布。

本研究中通過在狀態轉移方程中加入修正項，實現實時修正提議分布，使粒子集合更準確地“覆蓋”真實值，從而減弱粒子退化問題帶來的影響，提升狀態估計精度。基于時刻傳感器對縱向加速度、側向加速度及橫擺角速度的測量值（即和r_z）與時刻每一個粒子的縱向加速度、側向加速度及橫擺角速度值的差值對提議分布進行修正。提議分布修正項如下：

2.4改進粒子濾波估計器設計

對于固定參數的狀態估計器，在實際應用中，不可能針對每一種工況都分別調試出適合的參數，而只能兼顧各種常用工況來調試出一組折中的參數。因此，在工況變化時，固定參數估計器往往無法達到最佳的性能。為了保證估計器能夠在大多數工況下有效工作，提升估計器的魯棒性，本研究中對估計器的狀態轉移方程進行自適應設計以提高其工況適應能力^[17]：

估計器的觀測方程仍為式（13）。所提出的改進粒子濾波估計器完整算法以偽代碼形式表示如圖3所示。

算法1. 改進粒子濾波車速估計算法偽代碼

初始化濾波器：確定粒子數，仿真步長（采樣周期）和仿真時間

3仿真驗證分析

本研究中基于運動學模型設計了改進粒子濾波車速估計器，為了排除不同模型體系對車速估計精度的影響，選用文獻[17]中提出的基于運動學模型的粒子濾波估計器作為對照組，基于Matlab/Simulink和CarSim聯合仿真平臺，在雙移線工況和正弦轉角輸入工況下對設計的基于改進粒子濾波算法的車速估計器性能進行仿真驗證。

將CarSim軟件直接輸出的車速數據作為真實值，下文中簡稱實際值；將文獻[17]提出的自適應粒子濾波估計器產生的車速估計值稱為自適應粒子濾波估計值；將改進粒子濾波估計器產生的車速估計值稱為改進粒子濾波估計值。

3.1雙移線工況

在本工況中，設定車輛以120 km/h的車速勻速行駛，方向盤轉角輸入選擇CarSim中的“跟隨駕駛路徑-雙移線”選項（圖4），得到的仿真結果如圖5所示。由圖5可見，與自適應粒子濾波估計值相比，改進粒子濾波估計值更接近實際值。

進行50次蒙特卡洛仿真試驗后，自適應粒子濾波估計器和改進粒子濾波估計器的估計誤差結果如表1所示。可見，改進粒子濾波估計器產生的縱向速度估計值的平均絕對誤差、最大絕對誤差和均方根誤差比自適應粒子濾波估計器產生的相應誤差大幅降低，分別減小了40.25%、49.23%和25.63%。類似地，改進粒子濾波估計器產生的側向速度估計值的平均絕對誤差、最大絕對誤差和均方根誤差比自適應粒子濾波估計器產生的相應誤差分別減小了55.71%、54.23%和57.25%。在雙移線工況下，與自適應粒子濾波估計器相比，改進粒子濾波估計器的車速估計性能大幅提升。

3.2正弦轉角輸入工況

在本工況中，設定車輛以80 km/h的車速勻速行駛，方向盤轉角輸入為正弦波，如圖6所示。仿真時間設定為10 s，得到仿真結果如圖7所示。由圖7可見，與自適應粒子濾波估計值相比，改進粒子濾波估計值更接近實際值。

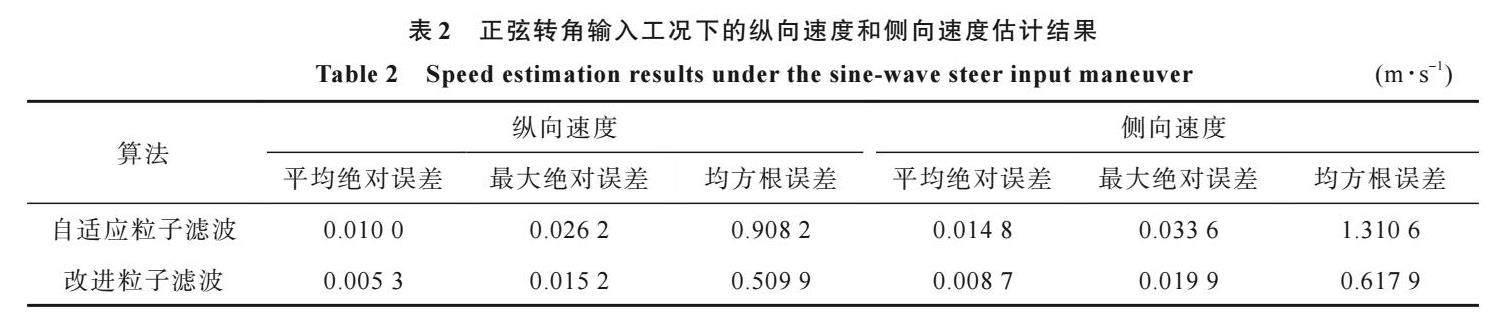
用自適應粒子濾波估計器和改進粒子濾波估計器進行50次蒙特卡洛仿真的估計誤差結果如表2所示。可見，改進粒子濾波估計器產生的縱向速度估計值的平均絕對誤差、最大絕對誤差和均方根誤差比自適應粒子濾波估計器產生的相應誤差分別減小了47.00%、41.98%和43.85%。類似地，改進粒子濾波估計器產生的側向速度估計值的平均絕對誤差、最大絕對誤差和均方根誤差比自適應粒子濾波估計器產生的相應誤差分別減小了41.21%、37.43%和52.85%。與雙移線工況類似，在正弦轉角輸入工況下，與自適應粒子濾波估計器相比，改進粒子濾波估計器的車速估計性能大幅提升。

4結束語

本研究中通過修正提議分布來減弱粒子濾波算法粒子退化問題對車速估計精度的影響。仿真結果表明，加入提議分布修正項后的粒子濾波估計器能夠在不同工況下準確、穩定地估計車輛的縱向速度和側向速度。與沒有修正提議分布的自適應粒子濾波估計器相比，改進后的粒子濾波估計器產生的平均絕對誤差、最大絕對誤差和均方根誤差均較小，車速估計精度得到較大的提升。

參考文獻

［1］??Zhao Z G， Chen H J， Yang J， et al. Estimation of the vehicle speed in the driving mode for a hybrid electric car based on an unscented Kalman filter[J]. Proceedings of the Institution of Mechanical Engineers， Part D： Journal of Automobile Engineering， 2015， 229（4）： 437-456.

［2］??余卓平， 高曉杰. 車輛行駛過程中的狀態估計問題綜述[J]. 機械工程學報， 2009， 45（5）： 20-33.

Yu Z P， Gao X J. Review of vehicle state estimation problem under driving situation[J]. Journal of Mechanical Engineering， 2009， 45（5）： 20-33. （in Chinese）

［3］??Daiss A， Kiencke U. Estimation of vehicle speed fuzzy-estimation in comparison with Kalman-filtering[C]//Proceedings of International Conference on Control Applications， September 28-29， 1995， Albany， NY， USA. IEEE， 1995： 281-284.

［4］??Moaveni B， Khosravi Roqaye Abad M， Nasiri S. Vehicle longitudinal velocity estimation during the braking process using unknown input Kalman filter[J]. Vehicle System Dynamics， 2015， 53（10）： 1373-1392.

［5］??王仁廣， 劉昭度， 齊志權， 等. 基于自適應卡爾曼濾波算法確定汽車參考車速[J]. 農業機械學報， 2006， 37（4）： 9-11， 41.

Wang R G， Liu Z D， Qi Z Q， et al. Vehicle reference speed determination using adaptive Kalman filter algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery， 2006， 37（4）： 9-11， 41. （in Chinese）

［6］??Guo H Y， Chen H， Xu F， et al. Implementation of EKF for vehicle velocities estimation on FPGA[J]. IEEE Transactions on Industrial Electronics， 2013， 60（9）： 3823-3835.

［7］??Park G， Choi S B， Hyun D， et al. Integrated observer approach using in-vehicle sensors and GPS for vehicle state estimation[J]. Mechatronics， 2018， 50： 134-147.

［8］??Wenzel T A， Burnham K J， Blundell M V， et al. Dual extended Kalman filter for vehicle state and parameter estimation[J]. Vehicle System Dynamics， 2006， 44（2）： 153-171.

［9］??張志勇， 張淑芝， 黃彩霞， 等. 基于自適應擴展卡爾曼濾波的分布式驅動電動汽車狀態估計[J]. 機械工程學報， 2019， 55（6）： 156-165.

Zhang Z Y， Zhang S Z， Huang C X， et al. State estimation of distributed drive electric vehicle based on adaptive extended Kalman filter[J]. Journal of Mechanical Engineering， 2019， 55（6）： 156-165. （in Chinese）

［10］??Chu L， Zhang Y S， Shi Y R， et al. Vehicle lateral and longitudinal velocity estimation based on unscented Kalman filter[C]//2010 2nd International Conference on Education Technology and Computer， June 22-24， 2010， Shanghai， China. IEEE， 2010： V3-427.

［11］??金賢建， 楊俊朋， 殷國棟， 等. 分布式驅動電動汽車雙無跡卡爾曼濾波狀態參數聯合觀測[J]. 機械工程學報， 2019， 55（22）： 93-102.

Jin X J， Yang J P， Yin G D， et al. Combined state and parameter observation of distributed drive electric vehicle via dual unscented Kalman filter[J]. Journal of Mechanical Engineering， 2019， 55（22）： 93-102. （in Chinese）

［12］??張志達， 鄭玲， 吳行， 等. 基于魯棒自適應UKF的分布式電動汽車狀態估計[J]. 中國科學： 技術科學， 2020， 50（11）： 1461-1473.

Zhang Z D， Zheng L， Wu H， et al. State estimation of distributed electric vehicle based on robust adaptive UKF[J]. Scientia Sinica （Technologica）， 2020， 50（11）： 1461-1473. （in Chinese）

［13］??Xin X S， Chen J X， Zou J X. Vehicle state estimation using cubature Kalman filter[C]//2014 IEEE 17th International Conference on Computational Science and Engineering， December 19-21， 2014， Chengdu， China. IEEE， 2014： 44-48.

［14］??李剛， 王野， 宗長富. 四輪輪轂電機電動汽車行駛狀態估計[J]. 汽車工程， 2018， 40（2）： 150-155.

Li G， Wang Y， Zong C F. Driving state estimation of electric vehicle with four-wheel-hub-motors[J]. Automotive Engineering， 2018， 40（2）： 150-155. （in Chinese）

［15］??樊東升， 李剛. 分布式驅動電動汽車行駛狀態估計綜述[J]. 汽車實用技術， 2019（16）： 10-12.

Fan D S， Li G. Review on driving state estimation of distributed drive electric vehicles[J]. Automobile Applied Technology， 2019（16）： 10-12. （in Chinese）

［16］??包瑞新， Edoardo S. 基于輔助粒子濾波算法的車輛行駛狀態和參數聯合估計方法研究[J]. 機械設計與制造， 2015（10）： 26-30.

Bao R X， Edoardo S. The research of state and parameter estimation under driving situation based on auxiliary particle filter method[J]. Machinery Design & Manufacture， 2015（10）： 26-30. （in Chinese）

［17］??Huang F H， Gao Y， Fu C Y， et al. Vehicle state estimation based on adaptive state transition model[C]//2020 4th CAA International Conference on Vehicular Control and Intelligence （CVCI）， December 18-20， 2020， Hangzhou， China. IEEE， 2020： 92-96.

［18］??姬鵬， 徐碩碩， 趙一凡， 等. 改進粒子濾波算法的車輛狀態估計研究[J]. 機械設計與制造， 2020（2）： 43-46， 50.

Ji P， Xu S S， Zhao Y F， et al. Research on vehicle state estimation based on improved particle filter algorithm[J]. Machinery Design & Manufacture， 2020（2）： 43-46， 50. （in Chinese）

［19］??靳彪. 輪轂電機驅動電動汽車狀態參數觀測及轉矩分配策略研究[D]. 北京： 北京交通大學， 2016.

Jin B. Research on state parameter observation and torque distribution strategy of electric vehicle driven by hub motor[D] . Beijing： Beijing Jiaotong University， 2016. （in Chinese）

［20］??李天成， 范紅旗， 孫樹棟. 粒子濾波理論、方法及其在多目標跟蹤中的應用[J]. 自動化學報， 2015， 41（12）： 1981-2002.

Li T C， Fan H Q， Sun S D. Particle filtering： theory， approach， and application for multitarget tracking[J]. Acta Automatica Sinica， 2015， 41（12）： 1981-2002. （in Chinese）

［21］??胡士強， 敬忠良. 粒子濾波算法綜述[J]. 控制與決策， 2005， 20（4）： 361-365， 371.

Hu S Q， Jing Z L. Overview of particle filter algorithm[J]. Control and Decision， 2005， 20（4）： 361-365， 371. （in Chinese）

［22］??Xu Y， Chen B Y， Chi C. Estimation of road friction coefficient and vehicle states by 3-DOF dynamic model and HSRI model based on information fusion[J]. Asian Journal of Control， 2018， 20（3）： 1067-1076.

［23］??黃小平， 王巖， 繆鵬程. 粒子濾波原理及應用： MATLAB仿真[M]. 北京： 電子工業出版社， 2017.

Huang X P， Wang Y， Miao P C. Particle filter principle and application： MATLAB simulation[M]. Beijing： Publishing House of Electronics industry， 2017. （in Chinese）

［24］??Panicker S， Gostar A K， Bab-Haidashar A， et al. Sensor control for selective object tracking using labeled multi-bernoulli filter[C]//2018 21st International Conference on Information Fusion （FUSION）， July 10-13， 2018， Cambridge， UK. IEEE， 2018： 2218-2224.

［25］??Li X R， Bar-Shalom Y. Design of an interacting multiple model algorithm for air traffic control tracking[J]. IEEE Transactions on Control Systems Technology， 1993， 1（3）： 186-194.

（編輯??羅敏）