等腰三角形考點直通車

凌泉

【摘要】等腰三角形是初中數學中的一個重要知識點，它的有關知識在平面幾何的計算和證明方面有非常廣泛的應用．近幾年的中考考題中，有關等腰三角形的考題出現得較多，考法也比較新穎．本文先對有關等腰三角形的考點進行概述，然后以例題的形式闡述等腰三角形考點的幾種常見考法，供學生復習備考時參考．

【關鍵詞】初中數學；等腰三角形；解題

1 等腰三角形重要考點概述

等腰三角形是初中數學中的一個重要知識點，現將涉及等腰三角形的中考考點加以闡述．第一，與等腰三角形性質有關的考點，主要有：等邊對等角（即等腰三角形的兩個底角相等）和三線合一（即等腰三角形的頂角平分線、底邊上的中線和底邊上的高互相重合）；第二，與等腰三角形判定有關的考點，主要有：“有兩邊相等的三角形是等腰三角形”和“有兩個角相等的三角形是等腰三角形（等角對等邊）”.

2 等腰三角形重要考點例析

2.1 根據等邊對等角求角度

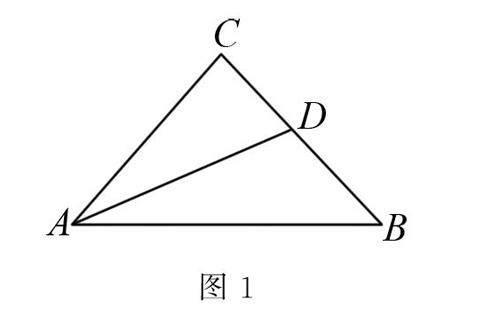
例1 如圖1所示，AD是△ABC的角平分線，AC=BC，∠ADC=60°，求∠C的度數．

解析 令∠BAD=x，

因為AD平分∠BAC，

所以∠CAD=∠BAD=x，∠BAC=2x（角平分線的定義），

因為AC=BC，

所以∠B=∠BAC=2x（等邊對等角），

又因為∠ADC=∠B+∠BAD（三角形外角的性質），

所以2x+x=60°，得x=20°，

所以∠B=∠BAC=40°，

在△ABC中，

因為∠BAC+∠B+∠C=180°，

所以∠C=100°．

點評 本題考查了等腰三角形的性質和角平分線的定義，根據等邊對等角求角度，學生熟練掌握各知識點是解題的關鍵．

2.2 根據等角對等邊求邊長

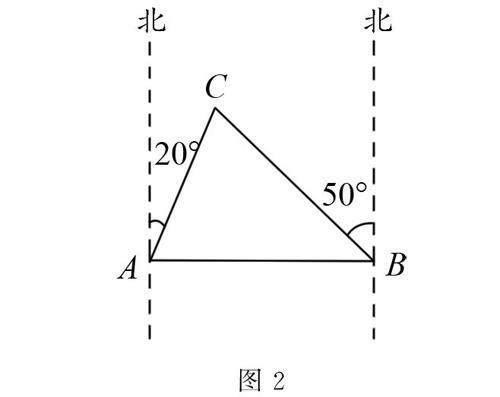
例2 如圖2所示，燈塔B在燈塔A的正東方向，且AB=75km．燈塔C在燈塔A的北偏東20°方向，燈塔C在燈塔B的北偏西50°方向．

（1）求∠ACB的度數；

（2）一輪船從B地出發向北偏西50°方向勻速行駛，5h后到達C地，求輪船的速度．

解析（1）根據題意得∠BAC=70°，

∠ABC=40°，

所以∠ACB=180°-∠BAC-∠ABC=

180°-70°-40°=70°.

（2）因為∠BAC=∠ACB=70°，

所以BC=AB=75km，

所以輪船的速度為v=BC/t=15km/h．

點評 本題考查方位角、等腰三角形的判定、三角形的內角和定理，學生熟練掌握等腰三角形的等角對等邊是解答本題的關鍵．

2.3 根據“三線合一”求解有關實際問題

例3 筼筜書院是廈門第一座現代書院，位于國家重點公園——白鷺洲公園東區．筼筜是竹之雅稱，書院以竹命名，自此鷺島貧筜湖畔于竹林環水，桃李繽紛之中，多了一處可供商量舊學，培養新知之地．如圖3所示，“筼筜書院”的頂端可看作等腰三角形ABC，AB=AC，D是邊BC上的一點．下列條件不能說明AD是△ABC的角平分線的是（）

（A）BD=CD.（B）∠ADB=∠ADC.

（C）S△ABD=S△ACD.（D）BC=2AD.

解析 因為△ABC是等腰三角形，AB=AC，

所以BD=CD，

所以AD是△ABC的角平分線，

故（A）選項不符合題意；

因為∠ADB+∠ADC=180°，

所以∠ADB=∠ADC=90°，

即AD是△ABC的高線，

因為△ABC是等腰三角形，AB=AC，

所以AD是△ABC的角平分線，

故（B）選項不符合題意；

因為S△ABD=S△ACD，

所以BD=CD，

所以AD是△ABC的角平分線，

故（C）選項不符合題意；

若BC=2AD，不能說明AD是△ABC的角平分線，故（D）選項符合題意.

點評 此題考查了等腰三角形的性質，學生重點掌握等腰三角形“三線合一”的性質是解答本題的關鍵．

2.4 根據“三線合一”證明

例4 如圖4所示，在△ABC中，AB=AC，點D，E分別為邊AB，AC上的點，DE∥BC，將△ABC沿DE對折，點A落在點A＇．

（1）請你根據圖形，利用無刻度的直尺作出邊BC的垂直平分線；

（2）請你運用所學的知識，證明所作的直線為邊BC的垂直平分線．

解析 （1）如圖5所示，直線AA＇即為BC的垂直平分線.

（2）由翻折可得AA＇⊥DE，

因為DE∥BC，

所以AA＇⊥BC，

因為AB=AC，

所以△ABC為等腰三角形，

所以直線AA＇即為BC的垂直平分線．

點評 本題考查了作圖、基本作圖、根據“三線合一”證明有關問題．

3 結語

等腰三角形是初中數學中的一個重要考點，掌握等腰三角形的性質和判定方法，能夠助力學生更好地解決相關的數學問題．同時，等腰三角形在實際生活中也有很廣泛的應用，例如在建筑設計、工程測量、物理學等領域都有廣泛的應用，應當引起學生的足夠重視．

參考文獻：

[1]王成棟.巧用等腰三角形的“三線合一”性質解題[J].現代中學生（初中版），2023（20）：33-34.

[2]鮑聰曉.等腰三角形重要題型解析[J].中學生數理化（八年級數學）（配合人教社教材），2023（10）：6-8.

[3]安娜.等腰三角形常見解題誤區[J].初中生世界，2023（15）：57.

[4]蔡建華.芻議等腰三角形問題中的分類討論[J].初中數學教與學，2023（07）：25-27.

[5]周貴勝.巧用等腰三角形旋轉解題[J].初中生學習指導，2022（33）：22-24.