STEAM教育理念下的初中數學應用題教學

王志華

摘 要：STEAM教育理念是指基于科學、技術、工程、藝術和數學這五個領域，通過跨學科的綜合性學習培養學生的創新思維和實踐能力.初中數學應用題教學是數學課堂中重要的一環，通過對數學概念的應用，培養學生的數學思維和解決問題的能力.將STEAM教育理念融合到初中數學應用題教學中，可以提高學生的興趣和參與度，也可以培養學生的創新思維和實踐能力.

關鍵詞：STEAM教育理念；初中數學；應用題

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2024）08-0049-03

由于初中生的生活經驗不足，掌握的數學知識有限，數學應用題往往會成為他們學習的難點.將STEAM教育理念融入初中數學應用題教學，能改變這樣的現狀.在實施STEAM教育理念下的數學應用題教學中，教師應借助其豐富的知識和技能，將不同學科的相關知識結合在一起，并與學生進行有效互動，使學生能夠協作、探究、創新和解決問題.這樣的教育方式既能夠滿足學生的興趣和需求，又能夠助力學生掌握更多的數學知識，并提升學生分析問題和解決問題的能力.

1 引導學生解析題目，展示習題特點

在STEAM教育理念下，初中數學教師可以通過以下幾個方面引導學生解析題目，展示習題特點.首先可采用學生為中心的教學方式，讓學生在小組合作中解析習題；其次幫助學生理解習題中的數學概念，同時與其他學科如工程、技術和藝術等相關概念進行關聯，以提升學生的跨學科思維能力；再次引導學生分析題目，把題目分解成更小的部分，理解其中各個部分之間的關系，從而探究出涉及的數學知識點.通過這樣的細分，學生可以更深入地理解問題，并更容易理解需要用到的數學知識點；最后借助多種教學資源，如圖表、演示文稿、視頻課等教學手段，幫助學生更好地理解題目，并將數學概念與日常生活、工程、技術、藝術等領域聯系起來[1].

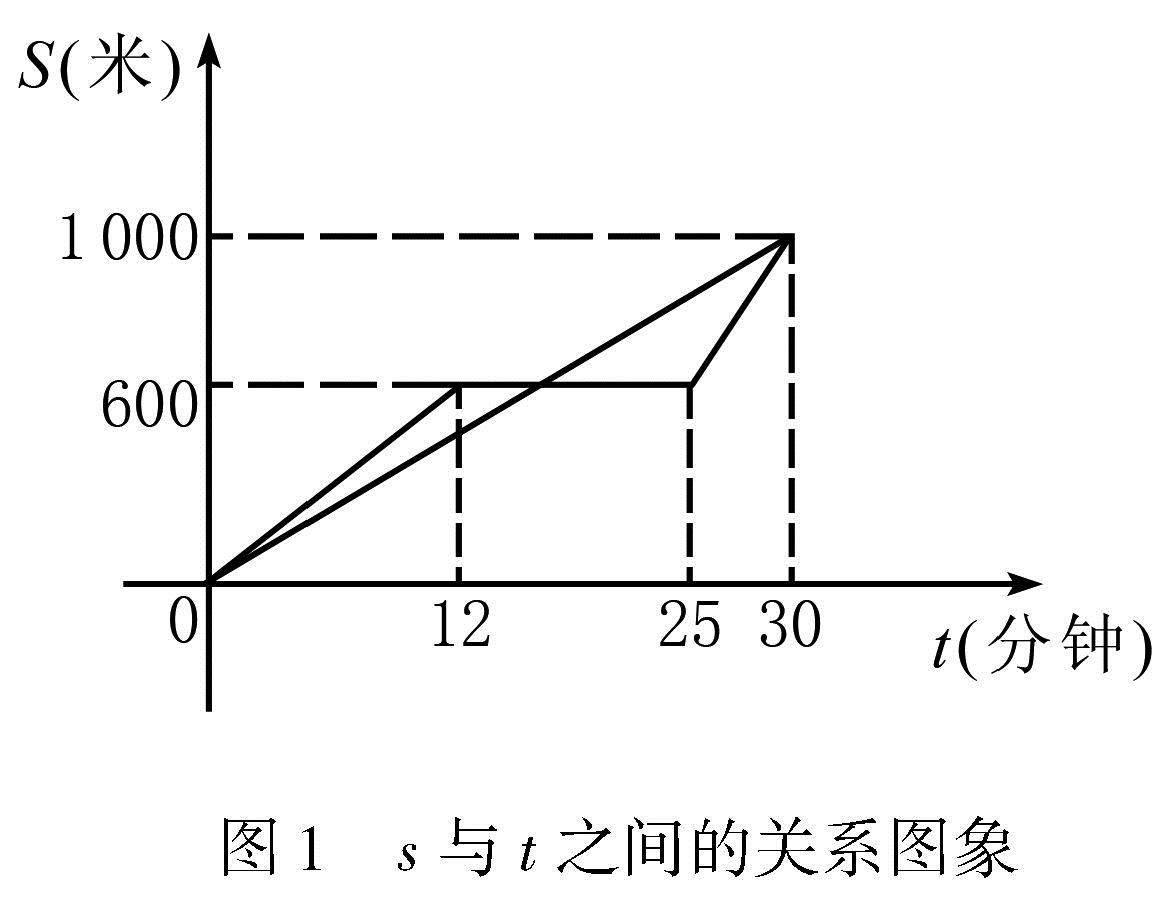
例1 如圖1所示，雙胞胎姐妹珊珊和雯雯在同一班讀書，周五16：00時放學后，珊珊和同學步行回家，途中沒有停留，雯雯騎車回家，她們各自與學校的距離s（米）與用去的時間t（分）之間的關系如圖所示，根據圖象提供的信息，你能得出哪些結論？

教師首先將學生分組，引導他們討論與生活相似的細節，再將題目中的表述與圖象結合起來，引導學生思考這道題主要考查他們哪些方面的認知.最后，教師可借助生活中的一些視頻，引導學生對接一次函數的圖象，再思考橫軸和縱軸表示的量，進而根據圖象提供的有關信息推斷一些與問題情境相關的結論.有的學生根據函數圖象右上端點的縱坐標推斷出，姐妹倆的家離學校1 000米；有的學生根據函數圖象右上端點的橫坐標推斷出姐妹倆同時到家，用時30 分鐘.珊珊離學校的距離s（米）與用去的時間t（分）的函數關系可知，推斷出她的速度為1 000

由此可見，在解決應用類問題時，教師可基于STEAM教育理念，提升學生認識應用題的特征和規律的能力，同時培養他們的創新能力和解決問題的能力[2].因此，教師要引導學生聯系實際情況，盡可能地汲取有用信息，這有助于學生更好地理解問題并解決問題.

2 引導學生仔細審題，展示審題過程

STEAM教育理念下的應用題教學要發揮學生的主體作用，讓他們在解決實際問題的過程中積累和提高數學素養.首先教師要提供有趣的實際問題，讓學生意識到解決問題的現實需求.這樣能夠激發學生的學習興趣，并加深學生的學習動機.其次，教師可以通過提問的方式引導學生發現問題的重點，讓學生明確問題的難點，從而在解題中有的放矢，更容易解決問題.最后，教師可以結合探究性學習、實驗等方法，幫助學生有目的地思考、解決問題，從而增強他們的自學能力和自信心.STEAM教育理念下的應用題教學要賦予學生更多的自主探究能力，激發學生對數學學科的興趣，全面提升數學素養和解決實際問題的能力.

例2 如圖2所示，△ABC為一塊田地，∠C=90°，AC=6米，BC=8米，現沿AD將其分為兩塊，若設DC=x米，△ABD的面積為y平方米，請求出y與x之間的函數關系式，并寫出自變量x的取值范圍；當x=6時，求△ABD的面積y.

在STEAM教育理念下，數學應用題的教學方法應該注重培養學生的解決問題能力，包括審題和獨立思考等方面.教師可以根據題目的特點設計有針對性的問題，引導學生針對性地分析、理解和解決問題.通過這種方式，學生可以逐漸養成精準思考和審題的好習慣，提高解題能力.同時，教師還可以根據學生的學習情況，針對性地提出問題，激發學生的興趣和學習動力，促進學生的理解和掌握知識的能力，從而提升其數學核心素養.

3 鼓勵學生一題多變，推動學生探究

一題多變是STEAM教育理念中的一個重要概念.在STEAM教育中，課堂教學活動要立足于實際問題，鼓勵學生在實際問題中探尋解決方法，通過這個過程，學生可以深入理解和掌握知識，并開發創造性思維.因此，在初中數學教學中，教師可以采用一題多變的教學方法，通過變異題目、加強練習、提高難度等手段，鼓勵學生深入探究問題本質，培養學生探究解決問題的能力.

例3 如圖3所示，在△ABC中，AB=10，BC=8，∠B=90°，將△ABC折疊，使A點與BC的中點D重合，折痕為MN，則線段BN的長是多少？

解析 根據圖形特征，設NB=x，則AN=10-x．由翻折的性質可知ND=AN=10-x.因為點D是BC的中點，所以BD=BC=4.在Rt△NBD中，由勾股定理可得ND2=NB2+DB2，即（10-x）2=x2+42，解得x=4.2，即BN=4.2.

基于以上求解方法，教師可讓學生歸納總結這類折疊問題的特點及求解方法.學生發現本題有兩個特點：一是原圖形是直角三角形；二是所折疊的三角形的一個頂點與原三角形一邊的中點重合.解決這類題時，不僅要運用勾股定理的相關知識，還要借助一元二次方程求解.基于這樣的思考，學生可得到本題的變式題.

變式 如圖4所示，在Rt△ABC中，∠C=90°，AC=BC，點D、E分別是邊AB、AC上的點，把△ADE沿DE折疊，點A恰好落在BC上的點F處，若點F為BC的中點，則CE：AC的值是多少？

對于變式問題，教師要引導學生發現它與原題目存在的不同點.學生發現最大的區別在于變式問題中的三角形為等腰三角形.學生進一步思考，如果過點F作FG⊥BD于點G，就能將BF與CF聯系起

由此可以看出，一題多變的教學方法也與STEAM教育中的綜合性解決問題的理念有關.采用一題多變的教學方法，教師能讓學生對數學問題有更全面的認識和理解，同時也可以培養學生的綜合性思維和解決問題的能力.在一題多變的過程中，學生需要更深入地思考問題的本質，從而提高學生解決問題和創新思維的能力[3].

4 結束語

在STEAM教育的理念引導下，初中數學應用題教學不再是單一、死板的知識傳授，而是將學科知識與學生的能力、生活等無縫融合的過程.在這一過程中，教師要將目光投向學生的個性化成長和綜合素質提升，不斷提高學生分析問題和解決問題的能力，提升學生的數學核心素養.

參考文獻：

［1］ 曹安寧.淺談初中數學應用題解題技巧能力的培養策略[J].考試周刊，2020（95）：57-58.

[2] 劉于標.以數學建模思想為基礎對初中數學應用題教學展開探究[J].數學學習與研究，2022（21）：38-40.

[3] 譚佳玥，王洪凱，馮曉青.基于STEAM教育理念的初中數學應用題教學策略研究[J].中學課程資源，2021，17（9）：31-34.