一維超冷原子動量光晶格中的手征對稱性破缺拓撲相*

曾超 毛一屹 吳驥宙 苑濤 戴漢寧? 陳宇翱

1) (中國科學技術大學物理學院,合肥微尺度物質科學國家研究中心,合肥 230026)

2) (中國科學技術大學,中國科學院量子信息與量子科技創新研究院,上海量子科學研究中心,上海 201315)

3) (合肥國家實驗室,合肥 230088)

4) (南方科技大學物理系,深圳 518055)

對稱性在理解物質的拓撲態方面具有關鍵作用.過去人們認為手征對稱性保證了一維晶格的量子化Zak 相位及其對應的非平庸拓撲相.本文展現了在一維手征對稱性破缺的情況下,晶格系統仍具有量子化Zak 相位和非平庸拓撲相.具體而言,在超冷原子動量晶格系統中有效地模擬了一個鏈長為26、手征對稱性破缺的Zigzag 模型,其中相等的次近鄰耦合強度能夠在保留空間反演對稱性的同時破壞手征對稱性.通過測量原子的時間平均波包位移來獲得系統的拓撲不變量,并得到了其對應的量子化的Zak 相位.此外,還觀測到系統隨著最近鄰耦合強度比例的變化會從非平庸拓撲相轉變為平庸拓撲相.本文不僅為對稱性及拓撲相的相關研究提供了一個完全可控的平臺,還可以通過控制格點間耦合強度和原子間相互作用,探索例如Tasaki,Aharonov-Bohm caging 模型中的平帶拓撲以及引入相互作用研究的非線性拓撲現象.

1 引言

二維電子氣體中的量子霍爾效應引入了拓撲相的概念[1,2],拓撲相的性質由物質的拓撲性質決定.由于拓撲相在凝聚態物理學[3]中的重要性以及在量子計算[4]、拓撲絕緣體[5]和其他材料科學領域[6]的潛在應用,拓撲相近年來備受關注.而拓撲類可以根據系統的維度和對稱性來區分[7],對稱性在拓撲相分類方面起關鍵作用.因此,開展對稱性及拓撲相的研究有助于理解拓撲材料的性質.在一維系統中,一般認為非平庸拓撲性受到了手征對稱性的保護[7,8].例如,在具有手征對稱性的Su-Schrieffer-Heeger (SSH)模型中[9],不同平臺的實驗結果已經表明SSH 模型確實具有量子化Zak 相位[10]及對應的非平庸拓撲相[11–13].特別地,在超冷原子系統中,人們利用光晶格模擬了SSH 模型并研究了模擬系統的拓撲性質,包括直接測量Zak相位[11],研究模型中受拓撲保護的邊界態的魯棒性[14],以及探索周期驅動的SSH 模型的拓撲性質[15]等.此外,在引入相互作用后還可以研究多體局域化[16]和非線性效應[17]等問題.

在SSH 模型中引入次近鄰耦合可以破壞其手征對稱性,對應的模型也被稱為Zigzag 模型[18–20].在一般的Zigzag 模型中,唯一剩下的對稱性就是時間反演對稱性.根據Altland-Zirnbauer 分類[21,22],系統處于AI類,無對稱性保護的非平庸拓撲相.通過設置次近鄰耦合強度相等,系統額外獲得了空間反演對稱性,此時系統具有對稱性保護的非平庸拓撲相[23].目前,人們僅在光子波導系統中對手征對稱性被破壞的一維系統的拓撲性質進行了實驗研究[24].而超冷原子系統具有精確可控與相互作用可調節的特性,是研究此問題的一個理想平臺,同時也有助于開展相互作用引起的拓撲態研究[25,26].

本文在一維超冷原子動量晶格實驗中,通過在SSH 模型中引入相等的次近鄰耦合,實現了鏈長為26 的手征對稱性破缺Zigzag 系統.利用原子的連續演化過程測量時間平均波包位移以獲得系統的拓撲不變量,從而得到相應的Zak 相位信息.同時,通過調節最近鄰耦合強度的比例,系統被調制在不同的拓撲物態中,通過時間平均波包位移的測量,觀測得到了系統由非平庸拓撲態向平庸拓撲態的轉變.本文為對稱性及拓撲相的相關研究提供了一個理想的實驗平臺,可進一步擴展對平帶及非線性拓撲的研究.

本文第2 節是Zigzag 模型的對稱性、拓撲不變量及拓撲態相關理論;第3 節在實驗上對Zigzag模型的拓撲不變量進行測量,并對系統的拓撲態進行分析;第4 節對超冷原子動量晶格中對稱性及拓撲態研究進行總結與展望.

2 理論部分

圖1(a)為本文要實現的一維Zigzag 晶格模型,該模型由兩種格點組成,這里分別被標記為A 和B.由于最近鄰耦合和次近鄰耦合的存在,粒子會在A 和B 之間、A 和A 之間以及B 和B 之間輸運.該系統的哈密頓量為

圖1 (a) 一維Zigzag 模型示意圖,格點之間的最近鄰耦合強度為 u1和u2,次近鄰耦合強度為 v1和v2 ;(b) Zigzag 模型的能帶分布圖;(c),(d)在系統不同的 u1/u2 情況下,Zigzag 模型的環繞數和Zak 相位的變化結果,參數為 v1=v2,v1/u2=0.4Fig.1.(a) Schematic diagram of a one-dimensional (1D) Zigzag model with nearest-neighbor coupling strengths u1 and u2 and next-nearest-neighbor coupling strengths v1 and v2 ;(b) band structure of the Zigzag model;(c),(d) variations of the winding number and Zak phase of the Zigzag model as a function of u1/u2,with parameters v1=v2 and v1/u2=0.4 .

其中,σ0是一個2 × 2 的單位矩陣,σ1,σ2和σ3是泡利矩陣.k為準動量,且-π ≤k≤π .可以求得系統能帶的能級色散關系:

圖1(b)為v1=v2,v1/u2=0.4且u1/u2=0.5的Zigzag 模型能帶圖.當v1=v20時,系統兩能帶的Zak 相位相等,此時Zak 相位γ和環繞數W滿足γ=πW.固定v1=v2,當u1u2時,系統的環繞數和Zak 相位均為0,系統處于平庸拓撲態,結果分別如圖1(c)和圖1(d)所示.

當v1=v20時,系統的手征對稱性被破壞,但系統仍然具備時間反演對稱性H?(-k)=H(k)和空間反演對稱性σ1H(-k)σ1=H(k) .根據具有空間反演對稱性的拓撲分類表[23]可知,AI 類且具有空間反演對稱性的系統存在非平庸拓撲相.具體到本系統的拓撲不變量而言,此時系統沒有σ3項,系統在布洛赫球表征下被限定σ1-σ2平面繞轉,因此系統的拓撲可以由其從一維動量空間到布洛赫球面上的一維空間映射的繞轉數確定,其繞轉數結果對應于系統的Zak 相位.

為了研究手征對稱性破缺系統的拓撲性,可以用一個可觀測的物理量來探測此系統的拓撲不變量,這里定義一個物理量平均波包位移:

其中,an(t)和bn(t) 是模型中第n個晶胞中A,B格點的占據振幅.對于一個無限長的演化時間T,時間平均波包位移(time-averaged mean displacement,TAMD)為[24,27]

因此,只要實驗上系統經過足夠長時間的演化,就可以通過測量TAMD 獲得對應的環繞數和Zak 相位.

3 實驗部分

圖2(a)的上部分為實驗上利用Bragg 過程實現一維動量晶格的示意圖[28].本文使用數量約為6×104的87Rb 的玻色-愛因斯坦凝聚體(Bose-Einstein condensate,BEC)原子,通過兩束波長λ 為1064 nm,波數k=2π/λ,頻率分別為ω+和的激光對向傳播并耦合出動量晶格的一系列動量態,其中ω+是單頻激光,是多頻激光.圖2(a)的下部分為實驗上利用時間飛行測量方法探測單格點的時間相關原子概率分布,通常選擇探測原子自由飛行24 ms 后的原子概率分布.

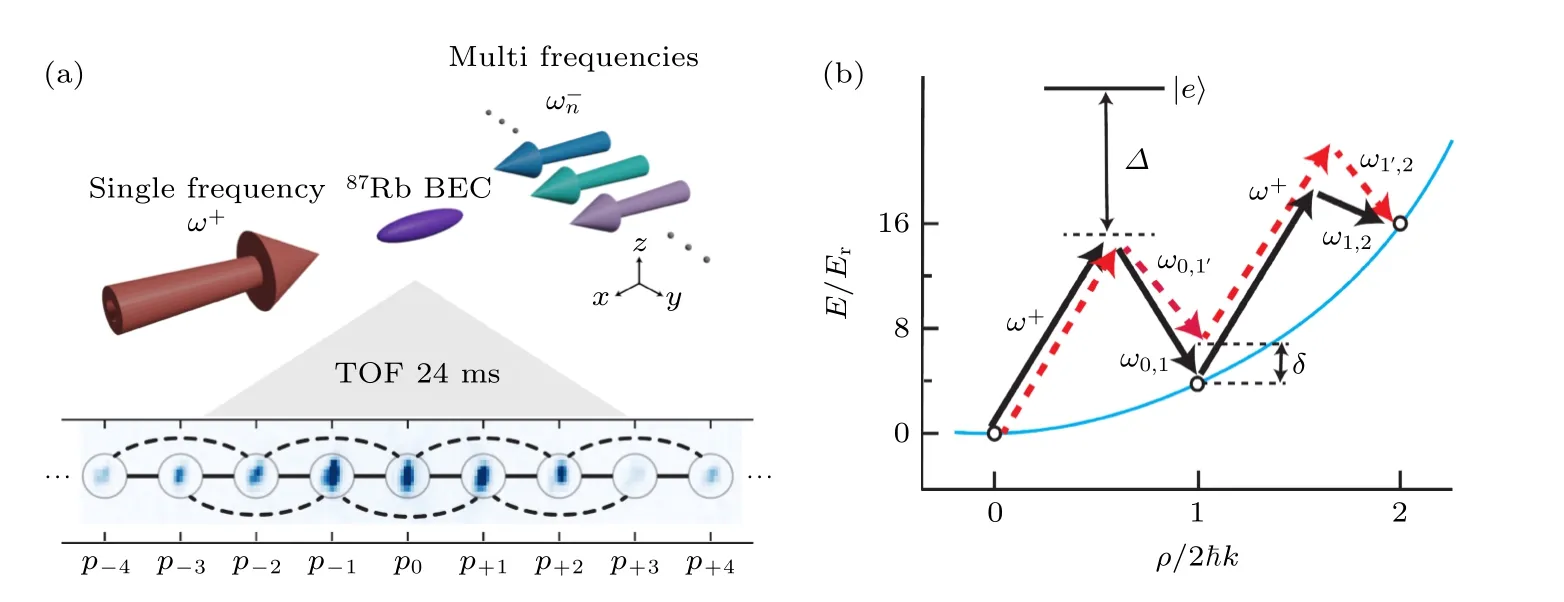
圖2 實現一維Zigzag 晶格(a)利用Bragg 過程實現一維動量晶格(上部分)和通過時間飛行成像探測原子數分布(下部分);(b)動量晶格中的原子色散曲線,分別利用一階和二階Bragg 躍遷耦合最近鄰和次近鄰格點Fig.2.Realization of 1D Zigzag lattice: (a) 1D momentum lattice realized using Bragg processes (upper part) and visualized via time-of-flight imaging (lower part);(b) atomic dispersion curve in the momentum lattice includes first-order and second-order Bragg transitions,which are used to couple the nearest-neighbor and next-nearest-neighbor lattice sites.

圖2(b)為動量晶格中最近鄰和次近鄰格點的耦合機制[29],可以通過一階和二階雙光子Bragg躍遷過程實現格點間最近鄰耦合和次近鄰耦合的精準調控.利用對打的兩束光耦合出一系列動量態作為動量晶格的格點,其對應的動量為pn=2n?k,反沖能量Er=?2k2/2mRb.對于最近鄰動量態p=0 和2?k的耦合,需要一階Bragg 共振(圖2(b)中實心黑色箭頭w+和w0,1)使兩個激光場的光子能量差與具有動量p=2?k的運動原子的附加動能相匹配,動量態p=2?k和p=4?k之間的耦合也類似.所以通過兩束具有合適頻率差的激光能耦合對應的最近鄰動量態pn和pn+1.而為了耦合次近鄰動量態,需要同時使用一階和二階Bragg 共振(圖2(b)中虛線紅色箭頭).對于次近鄰動量態p0和pn=4?k的耦合,需要一階Bragg 共振(圖2(b)中虛線紅色箭頭w+和w0,1′)和二階Bragg 共振(圖2(b)中虛線紅色箭頭w0,1′和w1′,2)共同實現,所以通過具有合適頻率差的激光能耦合對應的次近鄰動量態pn和pn+2.這里,?是單光子失諧量,而δ 是為了避免在次近鄰動量態耦合過程中對最近鄰動量態耦合產生影響設置的Bragg 雙光子躍遷過程失諧量.由于每個最近鄰或次近鄰耦合相關的動量態對應的頻率都是獨立的,所以Zigzag 模型的耦合強度、格點能量和耦合相位都可以通過激光的功率、頻率和相位進行單獨控制.

實驗上構建一個鏈長L=26 的Zigzag 系統,通過引入強度為v1=v2=0.15 kHz 的次近鄰耦合,使得系統只有空間反演對稱性和時間反演對稱性.這里先對一種平庸拓撲態的情況進行觀測,此時系統最近鄰耦合強度為u1=0.7kHz,u2=0.35 kH,圖3(a)為對應的原子在格點間的動力學演化,演化時長為3.1?/u2,時間間隔為0.11?/u2,實驗測量結果和數值模擬結果在整個演化過程中都基本符合.根據原子的演化過程可得u1/u2=2時的TAMD,如圖3(b)所示,系統的TAMD 在短時間內收斂至0 附近,且和數值模擬的收斂曲線基本符合.根據(5)式可知,對應的環繞數W以及Zak 相位都為0,系統此時處于平庸拓撲相.隨后也對一種非平庸拓撲態的情況進行觀測,此時系統最近鄰耦合強度u1=0.14kHz,u2=0.35 kHz,此條件下的原子在格點間的動力學演化過程如圖3(c)所示,整個演化過程中實驗和數值模擬結果都一致.同樣如圖3(d)所示,當u1/u2=0.4 時TAMD 收斂至–0.5 附近,此時W ≈-1 以及Zak相位為-π,系統處于非平庸拓撲相.

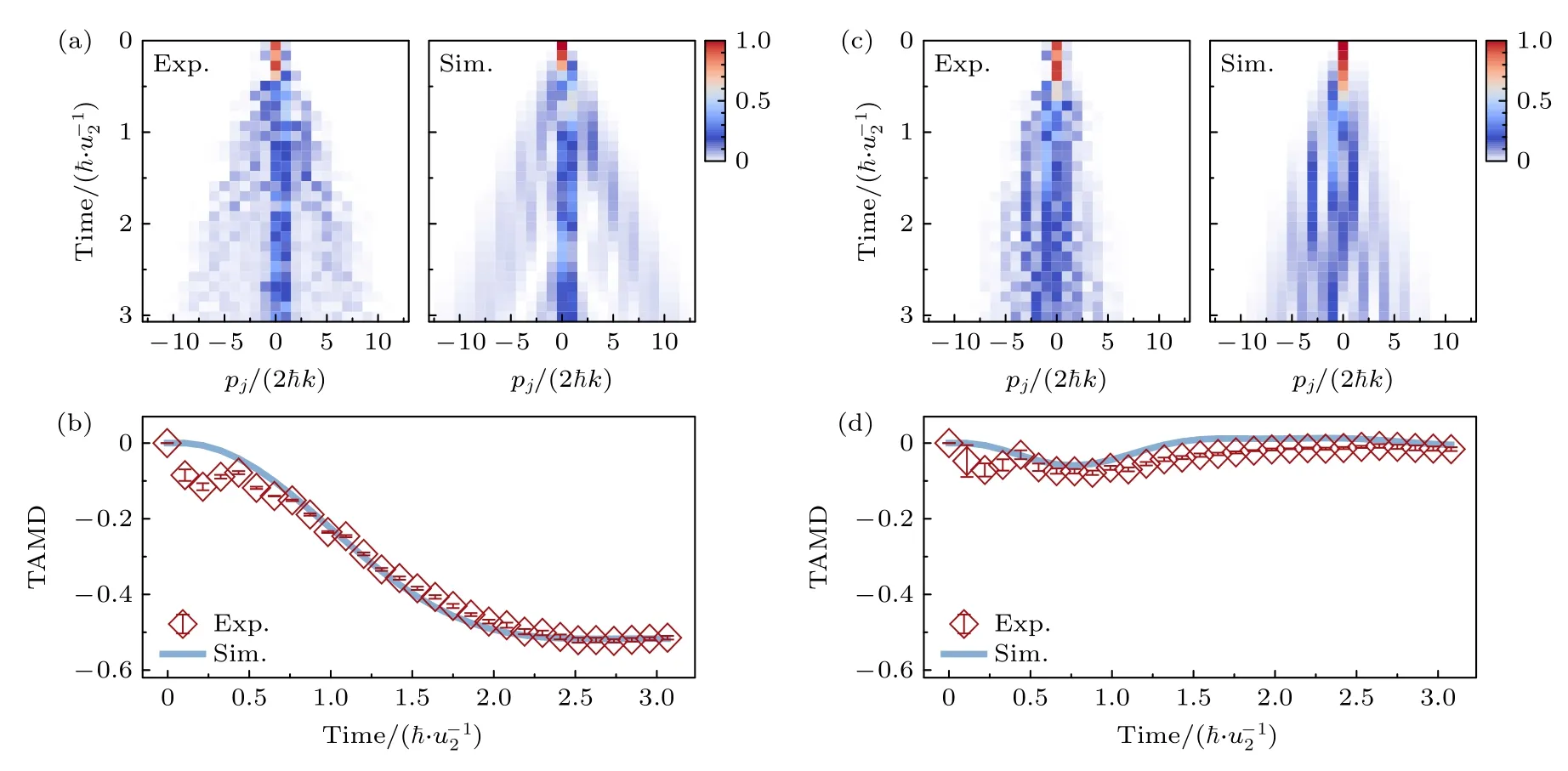
圖3 時間平均波包位移的測量(a) u1/u2=2時,系統的動力學演化過程,其中左圖為實驗結果,右圖為數值模擬結果;(b) 通過(5)式得到的圖(a)對應的TAMD 的演化結果;(c),(d) u1/u2=0.4時,測量得到的動力學演化過程和TAMD 演化結果.圖中采用的實驗參數: L=26,v1=v2=0.15kHz,u2=0.35kHz,演化時長為3.1?/u2,時間間隔為0.11?/u2Fig.3.Measurement of time-averaged wavepacket displacement: (a) Dynamics evolution of the system for u1/u2=2,where the left plot shows experimental results,and the right plot presents numerical simulations;(b) evolution of TAMD corresponding to panel (a) obtained using Eq.(5);(c),(d) dynamics evolution and TAMD results were obtained for u1/u2=0.4 .Experimental parameters: L=26,v1=v2=0.15kHz,u2=0.35kHz,an evolution time of 3.1?/u2,and a time interval of 0.11?/u2 .

為觀測系統從非平庸拓撲態到平庸拓撲態的轉變,對不同u1/u2情況的演化進行了測量,并計算得到了相應的TAMD.理想情況下,當u1/u2<1時,對應的TAMD 收斂值是–0.5,而當u1/u2>1時,對應的TAMD 是0.實驗上分別測量了L=26,u2=0.35kHz,v1=v2=0.15 kHz,演化時長為3.1?/u2的Zigzag 模型在u1/u2分別為0.05,0.2,0.4,0.6,0.8,1,1.2,1.4,1.6,1.8,2.0 時的TAMD.結果如圖4 所示,系統從u1/u2<1到u1/u2>1 過程中,TAMD 基本從–0.5 逐漸變成0,Zak 相位γ也從–π 轉變為0,對應的環繞數W也從–1 逐漸變成0,此時系統從非平庸拓撲相過渡到平庸拓撲相.因此,對于一個手征對稱性被破壞的一維晶格系統,其Zak 相位仍然是量子化且存在非平庸拓撲相.

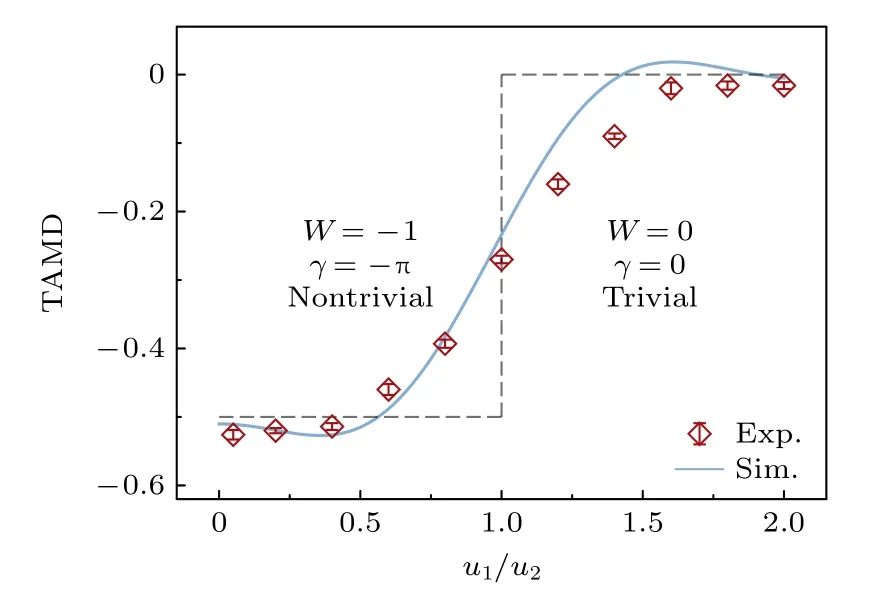
圖4 不同 u1/u2 的Zigzag 模型對應的TAMD 變化曲線.圖中灰色虛線是理想模型對應的結果Fig.4.Variation curves of TAMD for different u1/u2 in the Zigzag model.Gray dashed lines indicate results from the ideal model.

4 結論

本文研究了動量晶格系統中一維手征對稱性破缺晶格系統的拓撲性.實驗上利用87Rb 原子的BEC 模擬鏈長為26 的一維Zigzag 系統.通過調制激光功率使得所有次近鄰格點耦合強度都相等,此時系統手征對稱性被破壞.基于原子的連續演化過程測量時間平均波包位移以獲得系統的拓撲不變量,證明了一維手征對稱性破缺晶格系統仍具有量子化Zak 相位和非平庸拓撲相.此外,還觀測到在u1/u2=1時,系統從非平庸拓撲態轉變成平庸拓撲態.本工作為對稱性和拓撲相的相關研究提供了一個完全可控的平臺,可進一步引入相互作用研究非線性拓撲現象[17].此外,還可以用于研究基于SSH 模型的拓展模型.例如研究加上長程的格點耦合的拓展SSH 模型的相變臨界現象[30]和平帶能級結構[31],以及不同對稱性對拓展SSH 模型拓撲性質的影響[20].通過控制格點間耦合強度,探索具有更多能級結構的模型的拓撲性質,比如三能級結構的Aharonov-Bohm caging 模型[32–35]具有的奇異平帶性質.