核心素養(yǎng)導(dǎo)向的問題變式設(shè)計*
——以2023年高考新課標Ⅰ卷第16題為例

廣東省東莞高級中學(xué) (523128) 劉心華

一、問題提出

問題是發(fā)展學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)的平臺,看過問題三百個,不會解題也會問.《普通高中數(shù)學(xué)課程標準(2017年修訂版)》要求在數(shù)學(xué)學(xué)習(xí)中發(fā)展學(xué)生的數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運算、數(shù)據(jù)分析等學(xué)科核心素養(yǎng),教師應(yīng)結(jié)合教學(xué)任務(wù)及其蘊含的數(shù)學(xué)學(xué)科核心素養(yǎng)創(chuàng)設(shè)合適的情境和問題,引導(dǎo)學(xué)生用數(shù)學(xué)的眼光觀察現(xiàn)象、發(fā)現(xiàn)問題,使用恰當?shù)臄?shù)學(xué)語言描述問題,用數(shù)學(xué)的思想、方法解決問題.在問題解決的過程中,理解數(shù)學(xué)內(nèi)容的本質(zhì),促進學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)的形成和發(fā)展.

本文以2023年高考新課標Ⅰ卷第16題為例,探求問題解法并對問題進行變式設(shè)計,讓學(xué)生掌握一類橢圓(雙曲線)焦點三角形問題的解答、幾何性質(zhì)及一般解題方法,提升能力,感悟思想,積累經(jīng)驗,發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng).

二、試題解答

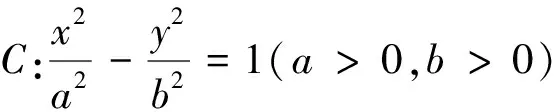
圖1

評注：解法1是從條件出發(fā),數(shù)形結(jié)合,把向量關(guān)系轉(zhuǎn)化為幾何等式,考察焦點△AF1F2與Rt△ABF1的邊角聯(lián)系,借助三角形的正(余)弦定理找到基本量a,b,c的齊次式,從而求解問題;解法2將問題坐標化,把向量關(guān)系轉(zhuǎn)化為坐標等式,借助雙曲線定義,通過坐標運算,找到基本量a,b,c的齊次關(guān)系求解問題.

三、變式設(shè)計

(一)變中求真,把握本質(zhì)

變式1 (2019年全國Ⅰ卷理10)已知橢圓C的焦點為F1(-1,0),F2(1,0),過F2的直線與C交于A,B兩點.若|AF2|=2|F2B|,|AB|=|BF1|,則C的方程為( ).

圖2

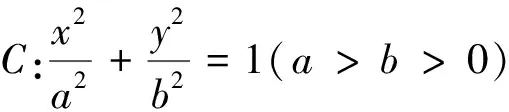
(2)若直線MN在y軸上的截距為2,且|MN|=5|F1N|,求a,b.

圖3

評注：以上變式問題從雙曲線到橢圓,由向量關(guān)系到長度……